重要: 对 Office 2016 和 Office 2019 的支持已于 2025 年 10 月 14 日结束。 升级到 Microsoft 365 以在任何设备上随时随地工作,并继续获得支持。 获取 Microsoft 365
本文讨论使用规划求解(一个可用于 What-if 分析的 Microsoft Excel 加载项程序)来确定最佳产品组合。
如何确定最大化盈利能力的每月产品组合?
公司通常需要确定每月要生产的每种产品的数量。 在最简单的形式中, 产品组合 问题涉及如何确定每个产品的数量,每个产品应在一个月内生产,以最大化利润。 产品组合通常必须遵守以下约束:
-
产品组合使用的资源不能超过可用资源。
-
每种产品的需求有限。 我们不能在一个月内生产出比需求更多的产品,因为过剩的生产被浪费 (例如易腐药物) 。
现在,我们来解决以下产品组合问题的示例。 可以在文件 Prodmix.xlsx 中找到此问题的解决方案,如图 27-1 所示。
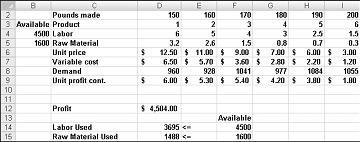
假设我们为一家制药公司工作,该公司在其工厂生产六种不同的产品。 每个产品的生产都需要人工和原材料。 图 27-1 中的第 4 行显示了生产每一磅产品所需的劳动时间,第 5 行显示生产每一磅产品所需的原材料磅。 例如,生产一磅产品 1 需要 6 小时的劳动力和 3.2 磅的原材料。 对于每种药物,每磅的价格在行 6 中给出,每磅的单位成本在行 7 中给出,每磅的利润贡献在行 9 中给出。 例如,Product 2 的售价为每磅 11.00 美元,每磅的单位成本为 5.70 美元,每磅贡献 5.30 美元的利润。 每一种药物的当月需求量在行 8 中给出。 例如,产品 3 的需求量为 1041 磅。 本月,有4500小时的劳动力和1600磅的原材料可用。 这家公司如何最大化其每月利润?
如果我们对 Excel 规划求解一无所知,我们将通过构建工作表来跟踪与产品组合关联的利润和资源使用情况来解决此问题。 然后,我们将使用试验和错误来改变产品组合,以优化利润,而不使用比可用更多的劳动力或原材料,并且不生产任何超过需求的药物。 在此过程中,我们仅在试错阶段使用规划求解器。 从本质上讲,规划求解是一个优化引擎,可以完美地执行试错搜索。
解决产品组合问题的关键是高效计算与任何给定产品组合相关的资源使用情况和利润。 可用于进行此计算的一个重要工具是SUMPRODUCT函数。 SUMPRODUCT 函数将单元格区域中的相应值相乘,并返回这些值的总和。 SUMPRODUCT计算中使用的每个单元格区域必须具有相同的维度,这意味着可以使用包含两行或两列的SUMPRODUCT,但不能包含一列和一行。
作为如何在产品组合示例中使用 SUMPRODUCT 函数的示例,让我们尝试计算资源使用情况。 我们的劳动力使用量按
(劳动使用每磅药物 1) * (毒品 1 磅生产) + (工党每磅药物2) * (毒品2磅生产) + ... (劳动每磅药物 6) * (毒品 6 磅生产)
我们可以以更乏味的方式计算劳动力使用情况 ,如 D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4。 同样,原材料使用量可以计算为 D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5。 但是,在六种产品的工作表中输入这些公式非常耗时。 想象一下,如果你与一家在工厂生产 50 种产品的公司合作,需要多长时间。 计算劳动力和原材料使用情况的一种更简单方法是将公式SUMPRODUCT ($D$2:$I$2,D4:I4) 从 D14 复制到 D15。 此公式计算 D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (这是我们的劳动力使用) 但更易于输入! 请注意,我使用范围为 D2:I2 的 $ 符号,以便在复制公式时,仍从第 2 行捕获产品组合。 单元格 D15 中的公式计算原材料使用情况。
以类似的方式,我们的利润取决于
(药物每磅 1 利润) * (药物 1 磅生产) + (药物 2 利润每磅) * (药物 2 磅生产) + ... (毒品 6 每磅利润) * (药物 6 磅生产)
使用公式 D9:I9,SUMPRODUCT ($D$2:$I$2) 在单元格 D12 中轻松计算利润。
现在,我们可以确定产品组合规划求解模型的三个组件。
-
目标单元格。 我们的目标是在单元格 D12) 中计算 (实现利润最大化。
-
更改单元格。 每个产品的磅数 (单元格范围 D2:I2)
-
约束。 我们具有以下约束:
-
不要使用比可用更多的劳动力或原材料。 也就是说,单元格 D14:D15 () 使用的资源的值必须小于或等于单元格 F14:F15 中的值, (可用资源) 。
-
不要生产比需求更多的药物。 也就是说,) 产生的每种药物的单元格 D2:I2 (磅的值必须小于或等于单元格 D8:I8) 中列出的每种药物的需求 (。
-
我们不能生产任何药物的负量。
-
我将演示如何在规划求解器中输入目标单元格、更改单元格和约束。 然后,只需单击“解决”按钮即可找到利润最大化的产品组合!
若要开始,请单击“数据”选项卡,然后在“分析”组中,单击“规划求解”。
注意: 如第 26 章“Excel 规划求解优化简介”中所述,通过依次单击“Microsoft Office 按钮、Excel 选项和加载项”来安装规划求解。 在“管理”列表中,单击“Excel 外接程序”,检查“规划求解加载项”框,然后单击“确定”。
将显示“规划求解参数”对话框,如图 27-2 所示。
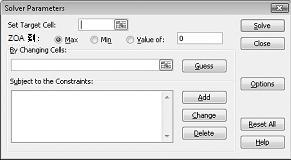
单击“设置目标单元格”框,然后选择利润单元格 (单元格 D12) 。 单击“通过更改单元格”框,然后指向范围 D2:I2,其中包含每种药物产生的磅数。 对话框现在应如图 27-3 所示。
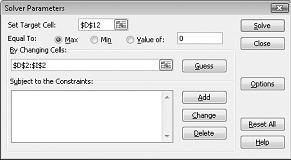
现在,我们已准备好向模型添加约束。 单击添加按钮。 你将看到“添加约束”对话框,如图 27-4 所示。
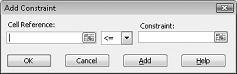
若要添加资源使用约束,请单击“单元格引用”框,然后选择范围 D14:D15。 从中间列表中选择 <= 。 单击“约束”框,然后选择单元格区域 F14:F15。 “添加约束”对话框现在应如图 27-5 所示。
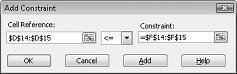
现在,我们已确保当规划求解尝试更改单元格的不同值时,仅满足 D14<=F14 (所用劳动力的组合小于或等于可用劳动力) 和 D15<=F15 (使用的原材料小于或等于可用原材料) 。 单击“添加”以输入需求约束。 填写“添加约束”对话框,如图 27-6 所示。
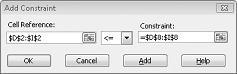
添加这些约束可确保当规划求解针对不断变化的单元格值尝试不同的组合时,仅考虑满足以下参数的组合:
-
D2<=D8 (药物 1 的产量小于或等于对药物 1 的需求)
-
E2<=E8 (药物 2 的产量小于或等于对药物 2 的需求)
-
F2<=F8 (药物 3 的产量小于或等于对药物 3 的需求)
-
G2<=G8 (药物 4 的产量小于或等于对药物 4 的需求)
-
H2<=H8 (药物 5 的产量小于或等于对药物 5 的需求)
-
I2<=I8 (药物 6 的产量小于或等于对药物 6 的需求)
在“添加约束”对话框中单击“确定”。 规划求解窗口应如图 27-7 所示。
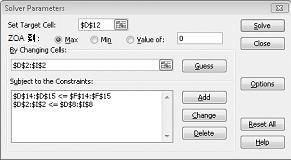
在“规划求解选项”对话框中输入更改单元格必须为非负数的约束。 单击“规划求解参数”对话框中的“选项”按钮。 选中“假设线性模型”框和“假设非负模型”框,如下一页上的图 27-8 所示。 单击“确定”。
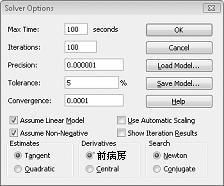
选中“假设非负值”框可确保规划求解仅考虑更改单元格的组合,其中每个更改单元格都假定非负值。 我们选中了“假设线性模型”框,因为产品组合问题是一种特殊类型的求解器问题,称为 线性模型。 从本质上讲,规划求解模型在以下条件下是线性的:
-
通过将 ( 更改单元格) * (常量) 的形式项相加来计算目标单元格。
-
每个约束都满足“线性模型要求”。 这意味着,通过将表单的项相加计算, (更改单元格) * (常量) 并将和与常量进行比较。
为什么此求解器问题呈线性关系? 我们的目标单元格 (利润) 计算为
(药物每磅 1 利润) * (药物 1 磅生产) + (药物 2 利润每磅) * (药物 2 磅生产) + ... (毒品每磅6利润) * (毒品6磅生产)
此计算遵循一种模式,即通过将 ( 更改单元格) * (常量) 的形式相加,来派生目标单元格的值。
我们的劳动约束是通过比较 每磅药物 1) * (每磅药物 1 磅产生的 (劳动力得出的值) + (每磅药物 2 使用的劳动力 (来评估的) * (毒品2磅生产) + ... (劳工我们每磅毒品6) * (毒品6磅生产) 劳动力可用。
因此,通过将表单的项相加计算, (更改单元格) * (常量) 并将和与常量进行比较。 劳动约束和原材料约束都满足线性模型要求。
我们的需求约束采用的形式
(药物 1 生产) <= (药物 1 需求) (药物 2 生产) <= (药物 2 需求) § (药物 6 生产) <= (药物 6 需求)
每个需求约束还满足线性模型要求,因为每个需求约束都是通过将表单的项相加来计算的, (更改单元格) * (常量) 并将和与常量进行比较。
在证明我们的产品组合模型是线性模型后,我们为什么要关心?
-
如果规划求解模型是线性的,并且我们选择了“假设线性模型”,则保证规划求解找到规划求解模型的最佳解决方案。 如果规划求解模型不是线性的,则规划求解可能找到最佳解决方案,也可能找不到最佳解决方案。
-
如果规划求解模型是线性的,并且我们选择了“假设线性模型”,则规划求解使用非常高效的算法 (单工方法) 来查找模型的最佳解决方案。 如果规划求解模型是线性的,并且我们不选择“假设线性模型”,则规划求解使用非常低效的算法 (GRG2 方法) ,并且可能难以找到模型的最佳解决方案。
在“规划求解选项”对话框中单击“确定”后,我们返回到“main规划求解”对话框,如图 27-7 所示。 单击“求解”时,规划求解会计算最佳解决方案 (是否存在) 产品组合模型。 正如我在第26章中指出的,产品组合模型的最佳解决方案是一组改变细胞值, (磅产生的每种药物) ,使所有可行解决方案的利润最大化。 同样,可行的解决方案是一组满足所有约束的更改单元格值。 图 27-9 中显示的不断变化的单元格值是一种可行的解决方案,因为所有生产级别都是非负的,生产级别不会超过需求,并且资源使用量不会超过可用资源。
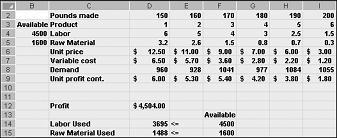
由于以下原因,下一页图 27-10 中显示的不断变化的单元格值表示 不可行的解决方案 :
-
我们生产的毒品 5 比对它的需求要多。
-
我们使用的劳动力比可用劳动力多。
-
我们使用的原材料比可用材料多。
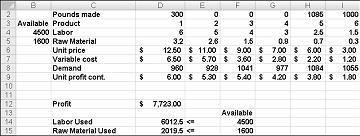
单击“求解”后,规划求解会快速找到图 27-11 所示的最佳解决方案。 需要选择“保留规划求解解决方案”,以保留工作表中的最佳解决方案值。
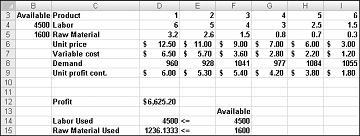
我们的制药公司可以通过生产596.67磅的药物4,1084磅药物5,没有其他药物,将每月利润最大化到6,625.20美元的水平! 我们无法确定是否可以通过其他方式实现 6,625.20 美元的最大利润。 我们所能保证的是,由于我们的资源和需求有限,本月的收入不可能超过6,627.20美元。
假设 必须 满足每个产品的需求。 (请参阅文件 Prodmix.xlsx.) 中的 “无可行的解决方案 ”工作表 然后,我们必须将需求约束从 D2:I2<=D8:I8 更改为 D2:I2>=D8:I8。 为此,请打开规划求解,选择 D2:I2<=D8:I8 约束,然后单击“更改”。 此时会显示“更改约束”对话框,如图 27-12 所示。
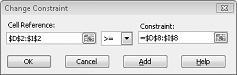
选择“>=”,然后单击“确定”。 我们现在已确保规划求解将仅考虑更改满足所有要求的单元格值。 单击“求解”时,会看到消息“规划求解找不到可行的解决方案”。 此消息并不意味着我们在模型中犯了错误,而是说,由于资源有限,我们无法满足所有产品的需求。 求解器只是告诉我们,如果我们想要满足每个产品的需求,我们需要增加更多的劳动力、更多的原材料,或者同时添加更多的原材料。
让我们看看,如果我们允许对每种产品无限需求,并且允许生产每种药物的负数量,会发生什么情况。 (可以在文件 Prodmix.xlsx.) 中的 “设置值不聚合” 工作表上看到此求解器问题 若要找到适合这种情况的最佳解决方案,请打开“规划求解”,单击“选项”按钮,并清除“假设非负值”框。 在“规划求解参数”对话框中,选择需求约束 D2:I2<=D8:I8,然后单击“删除”删除该约束。 单击“求解”时,规划求解返回消息“设置单元格值不收敛”。 此消息意味着,如果要将目标单元格最大化 (如示例中) 所示,则存在具有任意大目标单元格值的可行解决方案。 (如果要最小化目标单元格,则消息“设置单元格值不收敛”表示存在具有任意小目标单元格值的可行解决方案。) 在我们的情况下,通过允许负生产一种药物,我们实际上“创造”了可用于生产任意数量的其他药物的资源。 鉴于我们无限的需求,这使我们能够获得无限的利润。 在现实中,我们不能赚无限的钱。 简言之,如果看到“设置值不收敛”,则表示模型存在错误。
-
假设我们的制药公司可以购买最多 500 小时的劳动力,每小时比目前的劳动力成本多 1 美元。 我们如何实现利润最大化?
-
在芯片制造工厂, (A、B、C 和 D) 的四名技术人员 (产品 1、2 和 3) 生产三种产品。 本月,芯片制造商可以销售80台产品1,50台产品2,最多50台产品3。 技术人员 A 只能制造产品 1 和 3。 技术人员 B 只能制造产品 1 和 2。 技术人员 C 只能生产 Product 3。 技术人员 D 只能制造产品 2。 对于每个生产单位,产品贡献以下利润:产品1,6美元:产品 2,$7;和产品 3,$10。 每个技术人员制造产品) 需要 (小时的时间如下:
产品
技术人员 A
技术员 B
技术员 C
技术员 D
1
2
2.5
无法执行
无法执行
2
无法执行
3
无法执行
3.5
3
3
无法执行
4
无法执行
-
每个技术人员每月最多可以工作 120 小时。 芯片制造商如何最大化其每月利润? 假设可以生成小数个单位。
-
一家计算机制造厂生产鼠标、键盘和视频游戏游戏纵杆。 下表提供了每单位利润、每单位劳动力使用量、每月需求和每单位计算机时间使用情况:
鼠标
键盘
操纵 杆
利润/单位
$8
$11
$9
人工使用情况/单位
.2 小时
.3 小时
.24 小时
计算机时间/单位
.04 小时
.055 小时
.04 小时
每月需求
15,000
27,000
11,000
-
每个月共有 13,000 个劳动小时和 3000 小时的机器时间可用。 制造商如何最大化工厂的每月利润贡献?
-
解决我们的药物示例,假设必须满足每个药物的 200 个单位的最低需求。
-
杰森制作钻石手镯、项链和耳环。 他希望每月最多工作160小时。 他有800盎司的钻石。 下面提供了生产每种产品所需的利润、劳动时间和钻石盎司。 如果对每种产品的需求是无限的,Jason 如何最大化他的利润?
产品
单位利润
每个单位的工时数
每单位钻石盎司数
手镯
¥3,000
.35
1.2
项链
$200
.15
.75
耳环
¥100
.05
.5







