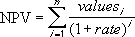NPV 函数

语法

NPV (rate，value1，value2...)

Rate     是一个时间段的折扣率。

Value1、value2,...     是表示付款和收入的 1 到 29 个参数。 Value1、value2,...必须在时间上相等，并且在每个周期结束时发生。 NPV使用 value1、value2 的顺序,...以解释现金流的顺序。 一定要按正确的顺序输入支出值和收益值。 对数字、空、逻辑值或数字的文本表示形式的参数进行计数;作为错误值或无法转换为数字的文本的参数将被忽略。

说明

• NPV 投资开始于 value1 现金流所在日期的前一期，并以列表中最后一笔现金流为结束。 NPV 的计算基于未来的现金流。 如果第一笔现金流发生在第一期的期初，则第一笔现金必须添加到 NPV 的结果中，而不应包含在值参数中。 有关详细信息，请参阅下面的示例。

• 如果 n 是值列表中现金流的笔数，则 NPV 的公式如下：

  

• NPV 类似于 PV 函数（现值）。 PV 与 NPV 的主要差别在于：PV 既允许现金流在期末开始也允许现金流在期初开始。 与可变的 NPV 的现金流值不同，PV 现金流在整个投资中必须是固定的。 有关年金与财务函数的信息，请参阅 PV。

示例 1

在以下示例中：

• 费率 是年度折扣率。

• Value1 是一年后的初始投资成本。

• Value2 是第一年的回报。

• Value3 是第二年的返回值。

• Value4 是第三年的回报。

在本示例中，将初始 10,000 美元成本作为值之一，因为付款发生在第一个周期结束时。

示例 2

在以下示例中：

• 费率 是年度折扣率。 可表示整个投资的通货膨胀率或利率。

• Value1 是一年后的初始投资成本。

• Value2 是第一年的回报。

• Value3 是第二年的返回值。

• Value4 是第三年的回报。

• Value5 是第四年的回报。

• Value6 是第五年的回报。

在此示例中，不会将初始 40,000 美元成本作为值之一，因为付款发生在第一个周期的开头。