重要: 我們將於 2025 年 10 月 14 日終止對 Office 2016 和 Office 2019 的支援。 升級至 Microsoft 365 即可隨時隨地在任何裝置上工作,並繼續獲得支援。 取得 Microsoft 365
本文討論如何使用 Microsoft Excel 載入巨集程式「規劃求解」來判斷最佳的產品群組。
如何判斷能最大化獲利的每月產品群組?
公司通常需要判斷每個產品每月生產的數量。 在最簡單的形式中, 產品混合 式問題涉及如何判斷一個月內應生產的每項產品量,以最大化利潤。 產品群組通常必須遵守下列限制式:
-
產品混合無法使用超過可用的資源。
-
每個產品的需求有限。 我們無法在一個月內產生比需求更多的產品,因為多餘的生產會浪費 (例如,易於消失的毒) 。
現在就讓我們來解決下列產品混合問題範例。 您可以在檔案 Prodmix.xlsx 中找到此問題的解決方案,如圖 27-1 所示。
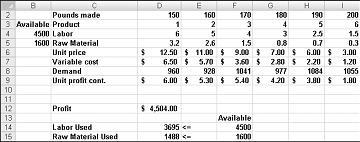
假設我們為一家公司工作,該公司在其工廠生產六種不同的產品。 每項產品的生產需要人力和原始材料。 圖 27-1 中的第 4 列顯示產生每項產品一磅所需的工時,列 5 顯示產生每項產品一磅所需的材料磅。 例如,生產一磅產品 1 需要 6 小時的人力和 3.2 磅的材料。 針對每位商品,每磅的價格是在第 6 列提供,每磅的單位成本是在第 7 列指定,而每磅的獲利額則在第 9 列提供。 例如,產品 2 的銷售價格為每磅 $11.00 美元、產生每磅 $5.70 的單一成本,併產生每磅 $5.30 美元利潤。 每項藥用量的月份需求是在第 8 列提供。 例如,產品 3 的需求是 1041 磅。 這個月可使用 4500 小時的人力和 1600 磅的材料。 該公司如何最大化其每月利潤?
如果我們對 Excel 規劃求解一無任何了解,我們就會建構工作表來追蹤與產品群組相關聯的利潤和資源使用量來攻擊此問題。 然後我們會使用試用版和錯誤來改變產品群組,以優化利潤,而不會使用超過可用數量的人力或原始材料,而且不會產生任何超過需求的消費量。 在此程式中,我們只會在試用與錯誤階段使用規劃求解。 基本上,規劃求解是一個優化引擎,完美地執行試用和錯誤搜尋。
解決產品混合式問題的一個關鍵,是有效率地計算與任何指定產品群組相關聯的資源使用量和利潤。 我們可以用來進行此計算的重要工具是 SUMPRODUCT 函數。 SUMPRODUCT 函數會將儲存格範圍中的對應值相乘,並傳回這些值的總和。 在 SUMPRODUCT 評估中使用的每個儲存格範圍都必須有相同的維度,這表示您可以將 SUMPRODUCT 搭配兩列或兩欄使用,但不能使用一欄和一列。
舉例來說,我們如何在產品混合型範例中使用 SUMPRODUCT 函數,讓我們嘗試計算我們的資源使用量。 我們的工時使用量是以
(每磅消費 1) * (次要稅 1 磅的工時使用,) + (工時每磅消費 2) * (生產 2 磅,) + ... (工時每磅消費 6) * (生產 6 磅,)
我們可以使用 D2*D4+E2*E4+F2*F4+F4+G2*G4+H2*H4+I2*I4 等較為單調的方式來計算人力使用量。 同樣地,材料使用量可以計算為 D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5。 不過,在六種產品的工作表中輸入這些公式是很耗時的。 假設您與一家生產了50家工廠產品的公司合作,需要多久時間。 計算人力和原始材料使用量的簡單方法是將公式從 D14 複製到 D15,SUMPRODUCT ($D$2:$I$2,D4:I4) 。 此公式會計算 D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (這是我們的人力使用量) 但輸入起來容易得多! 請注意,我使用 $符號搭配範圍 D2:I2,這樣當我複製公式時,仍然會從第 2 列擷取產品混合。 單元格 D15 中的公式會計算原始材料使用量。
在類似的方式中,我們的利潤是由
(每磅獲利 1) * (生產量 1 磅) + (每磅獲利 2 磅) * (量 2 磅) + ... (每磅獲利 6) * (生產量 6 磅)
在單元格 D12 中輕鬆計算利潤,且公式 SUMPRODUCT (D9:I9,$D$2:$I$2) 。
我們現在可以識別產品混合式規劃求解模型的三個元件。
-
目標儲存格。 我們的目標是在儲存格 D12) 中最大化利潤 (計算。
-
變更儲存格。 單元格範圍 D2:I2) 中列出的每個產品 (產生的磅數
-
約束。 我們有下列限制式:
-
請勿使用超過可用的工時或原始材料。 也就是說,單元格 D14:D15 中的值 () 使用的資源必須小於或等於單元格 F14:F15 中的值, (可用資源) 。
-
不要產生比需求更多的農用藥材。 也就是說,單元格 D2:I2 中所產生的值 (磅) 必須小於或等於單元格 D8:I8) 中列出的每個次要 (的需求。
-
我們無法產生任何金額的負值。
-
我要告訴您如何在規劃求解中輸入目標儲存格、變更儲存格和限制式。 您只需要按兩下 [求解] 按鈕,尋找獲利最大化的產品群組!
若要開始,請按兩下 [數據] 索引標籤,然後按兩下 [分析] 群組中的 [規劃求解]。
附註: As explained in Chapter 26, "An Introduction to Optimization with Excel Solver," Solver is installed by clicking the Microsoft Office Button, then Excel Options, followed by Add-Ins. 在 [管理] 清單中,按兩下 [Excel 載入巨集],核取 [規劃求解載巨集] 方塊,然後按兩下 [確定]。
[規劃求解參數] 對話框隨即出現,如圖 27-2 所示。
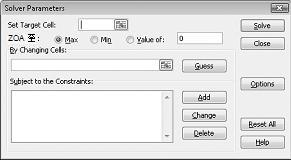
單擊 [設定目標儲存格] 方塊,然後在儲存格 D12) (選取我們的利潤單元格。 按兩下 [經由變更儲存格] 方塊,然後指向範圍 D2:I2,其中包含每項儲存量所產生的磅數。 對話框現在應該會顯示為圖 27-3。
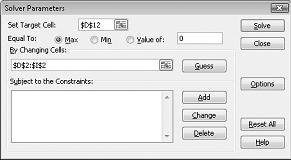
我們現在已準備好在模型中新增限制式。 按兩下 [新增] 按鈕。 您會看到 [新增限制式] 對話框,顯示在圖 27-4 中。
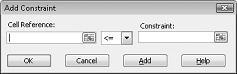
若要新增資源使用限制式,請按兩下 [單元格參照] 方塊,然後選取範圍 D14:D15。 從中間清單中選取 <= 。 按兩下 [限制式] 方塊,然後選取單元格範圍 F14:F15。 [新增限制式] 對話框現在看起來應該像圖 27-5。
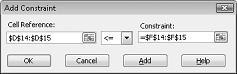
我們現在已確保當規劃求解針對變更的單元格嘗試不同的值時,只會考慮只滿足 D14<=F14 (使用之人力小於或等於可用) 的工時,且 D15<=F15 (使用的原始材料小於或等於可用) 的原始材料。 按兩下 [新增] 以輸入需求限制式。 如圖 27-6 所示,填入 [新增限制式] 對話框。
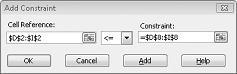
新增這些限制式可確保當規劃求解針對變更的儲存格值嘗試不同的組合時,只會考慮符合下列參數的組合:
-
D2<=D8 (方塊 1 的產生量小於或等於對維他性 1)
-
E2<=E8 (方塊 2 的生產量小於或等於對活期 2)
-
F2<=F8 (3 的製作量小於或等於對 3)
-
G2<=G8 (製作 4 的生產量小於或等於對工作 4)
-
H2<=H8 (5 製作量小於或等於 5)
-
I2<=I8 (製作 6 的量小於或等於 6)
按兩下 [新增限制式] 對話框中的 [確定]。 [規劃求解] 視窗看起來應該像圖 27-7。
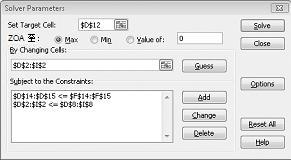
我們在 [規劃求解選項] 對話框中輸入變更儲存格必須非負數的限制式。 按兩下 [規劃求解參數] 對話框中的 [選項] 按鈕。 核取 [假設線性模型] 方塊和 [假設非負數] 方塊,如下一頁的圖 27-8 所示。 按一下 [確定]。
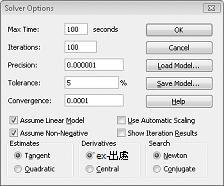
核取 [假設非負數] 方塊可確保 [規劃求解] 只會考慮變更單元格的組合,其中每個變更的單元格都會假設非負值。 我們核取了 [假設線性模型] 方塊,因為產品混合問題是稱為 線性模型的特殊規劃求解問題類型。 基本上,規劃求解模型在下列情況下是線性的:
-
目標儲存格的計算方式是將表單的詞彙加總 (變更儲存格) * (常數) 。
-
每個限制式都滿足「線性模型需求」。 這表示每個限制式的評估方式是將表單的詞彙相加 (變更儲存格) * (常數) ,並比較加總至常數。
為什麼此規劃求解問題橫線? 我們的目標儲存格 (利潤) 計算為
(每磅獲利 1) * (生產量 1 磅) + (每磅獲利 2 磅) * (量 2 磅) + ... (每磅獲利 6) * (次要產品 6 磅)
此計算遵循一種模式,藉由將窗體的字詞加總,將目標單元格的值匯出 , (變更單元格) * (常數) 。
我們的人力限制式是藉由比較衍生自「 1) * (每磅所用的「 (工」1 磅,產生) + (「工夫」每磅二) * (產生兩磅) + ... (工夫我們每磅 6) * (每磅產生的 6 磅,) 產生給 有空的工夫。
因此,會將表單的詞彙加總 (變更單元格) * (常數) ,並將總和與常數進行比較,藉此評估這種限制式。 工時限制式和原始材料限制式均符合線性模型需求。
我們的需求限制式採用表單
(量 1 生產) <= (量 1 需求) (出自變數 2 生產) <= (次性 2 需求) § (生產過的 6) <= (6 需求)
每個需求限制式也滿足線性模型需求,因為每一項都是透過將表單的詞彙相加來評估 , (變更單元格) * (常數) 並比較總和至常數。
顯示我們的產品混合模型是線性模型,為什麼我們該小心?
-
如果規劃求解模型是線性的,而我們選取 [假設線性模型],[規劃求解] 就可保證找到規劃求解模型的最佳解決方案。 如果規劃求解模型不是線性,規劃求解可能會或可能找不到最佳的解決方案。
-
如果規劃求解模型是線性的,而我們選取 [假設線性模型],規劃求解會使用非常有效率的演算法, (簡易方法) 來尋找模型的最佳解決方案。 如果規劃求解模型是線性的,而我們並未選取 [假設線性模型],規劃求解會使用非常低效的演算法 (GRG2 方法) ,而且可能無法找到模型的最佳解決方案。
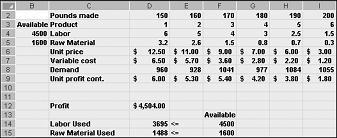
在 [規劃求解選項] 對話框中按兩下 [確定] 之後,我們返回 [主要規劃求解] 對話框,如圖 27-7 稍早所示。 當我們按兩下 [求解] 時,[規劃求解] 會 (我們的產品混合模型) 一個解決方案時,計算出最佳的解決方案。 如我在第 26 章所述,產品混合模型的最佳解決方案是一組變更單元格值, (每項殘留) 產生的磅,以最大化一組可行解決方案的利潤。 同樣地,可行的解決方案是一組符合所有限制式的儲存格值變更。 變更圖 27-9 中顯示的儲存格值是可行的解決方案,因為所有生產層級都是非負數、生產層級不會超過需求,且資源使用量不會超過可用資源。
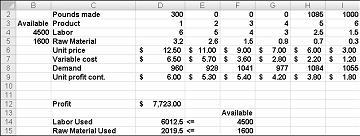
下一頁圖表 27-10 中顯示的變更儲存格值代表下列不可 行的解決方案 :
-
我們產生的「啟動 5」比對它的需求還多。
-
我們使用的人力超過可用的人力。
-
我們的原始材料使用量超過可用量。
按兩下 [求解] 之後,[規劃求解] 會快速找到圖 27-11 中顯示的最佳解決方案。 您必須選取 [保留規劃求解解決方案],才能在工作表中保留最佳的解決方案值。

我們的電池公司能以 $6,625.20 為單位最大化其每月利潤,方法是生產 596.67 磅的稅金 4、1084 磅的毒體 5,而且沒有其他的毒藥! 我們無法以其他方式判斷是否能達到 $6,625.20 的最大利潤。 我們只能確定,在有限的資源和需求下,本月無法取得超過 $6,627.20 的金額。
假設您 必須 滿足每個產品的需求。 (請參閱檔案 Prodmix.xlsx.) 中的 不可行解決方案 工作表 接著我們必須將需求限制式從 D2:I2<=D8:I8 變更為 D2:I2>=D8:I8。 若要這麼做,請開啟 [規劃求解],選取 D2:I2<=D8:I8 限制式,然後按兩下 [變更]。 [變更限制式] 對話框隨即出現,顯示在圖 27-12 中。
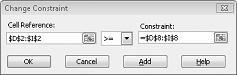
選 >=,然後按下 [確定]。 我們現在已確保規劃求解會考慮只變更符合所有需求的單元格值。 按兩下 [求解] 時,您會看到「規劃求解找不到可行的解決方案」訊息。 這則訊息並不表示我們在模型中做了錯誤,而是因為我們的資源有限,因此無法滿足所有產品的需求。 「規劃求解」只是告訴我們,如果我們想要滿足每個產品的需求,我們需要新增更多人力、更多原始材料,或兩者都增加更多。
讓我們看看如果我們允許每項產品無限制的需求,並且允許每項商品產生負數量,會發生什麼情況。 (您可以在檔案中的 [ 設定值不集中 ] 工作表上看到此規劃求解問題 Prodmix.xlsx.) 若要尋找此情況的最佳解決方案,請開啟 [規劃求解],按兩下 [選項] 按鈕,然後清除 [假設非負數] 方塊。 在 [規劃求解參數] 對話框中,選取需求限制式 D2:I2<=D8:I8,然後按兩下 [刪除] 移除限制式。 當您按兩下 [求解] 時,規劃求解會傳回「設定單元格值不要集中」訊息。 這則訊息表示,如果目標儲存格要最大化 (如我們的範例) ,則有任意大型目標單元格值的可行解決方案。 (如果要將目標儲存格最小化,「設定儲存格值請勿集中」訊息表示有可行的解決方案,包含任意小目標單元格值。) 在我們的情況中,藉由允許負果生產,實際上我們「建立」資源,可用來產生大量的其他毒物。 根據我們的無限需求,這可讓我們獲得無限制的利潤。 在實際情況中,我們無法賺到無限的金額。 簡而言之,如果您看到「設定值不要集中」,您的模型就會發生錯誤。
-
假設我們的農用公司最多可以以每小時 $1 美元比目前的人力成本購買 500 小時的工時。 如何最大化利潤?
-
在晶元製造廠,4 名技術人員 (A、B、C 和 D) 生產產品 1、2 和 3) (三種產品。 這個月,晶元製造商可以銷售產品 1 的 80 個裝置、產品 2 的 50 個裝置,以及最多 50 個產品 3 的裝置。 技術人員 A 只能製作產品 1 和 3。 技術人員 B 只能製作產品 1 和 2。 技術人員 C 只能製作產品 3。 技術人員 D 只能製作產品 2。 針對所生產的每一個單位,產品會獲得下列利潤:產品 1、$6;產品 2、$7;和產品 3,$10。 每位技術人員在小時) 製造產品所需的時間 (如下:
產品
技術人員 A
技術人員 B
技術人員 C
技術人員 D
1
2
2.5
無法執行
無法執行
2
無法執行
3
無法執行
3.5
3
3
無法執行
4
無法執行
-
每位技術人員每個月最多可以工作 120 小時。 晶片製造商如何最大化其每月利潤? 假設可以產生小數的單位。
-
計算機製造廠生產滑鼠、鍵盤和視訊遊戲遊戲桿。 下表提供單位利潤、單位工時使用量、每月需求及每單位計算機使用時間使用量:
滑鼠
鍵盤
操縱桿
利潤/單位
$8
$11
9 美元
工時使用量/單位
.2 小時
.3 小時
.24 小時
計算機使用時間/單位
.04 小時
.055 小時
.04 小時
每月需求
15,000
27,000
11,000
-
每個月總共有 13,000 個工時和 3000 小時的電腦使用時間。 製造商如何將工廠的每月利潤貢獻最大化?
-
解決我們的註冊範例,假設必須滿足每種藥體的最低需求 200 單位。
-
Jason 會製作菱形大括弧、項鍊和耳環。 他想要每月最多工作 160 小時。 他擁有800盎司的菱形。 以下提供生產每個產品所需的利潤、工時和一盎司菱形。 如果每個產品的需求是無限的,Jason 該如何最大化其利潤?
產品
單位利潤
每個單位的工時
每單位一盎司菱形
手鐲
$300
.35
1.2
項鍊
$200
.15
.75
耳環
$100
.05
.5










