Devolve a probabilidade de distribuição binomial de termo individual. Utilize a DISTRBINOM em problemas com um número fixo de testes ou tentativas, quando o resultado desejado for apenas sucesso ou falha; quando as tentativas forem independentes e quando a probabilidade de sucesso for constante ao longo da experiência. Por exemplo, DISTRBINOM pode calcular a probabilidade de que dois em três bebés nascidos sejam do sexo masculino.
Importante: Esta função foi substituída por uma ou mais novas funções que podem fornecer uma maior exatidão e cujos nomes refletem melhor a respetiva utilização. Embora esta função ainda esteja disponível para retrocompatibilidade, deve considerar a utilização das novas funções a partir de agora pois a mesma pode não estar disponível em versões futuras do Excel.
Para obter mais informações sobre a nova função, consulte Função DISTR.BINOM.
Sintaxe
DISTRBINOM(número_s;tentativas;probabilidade_s;cumulativo)
A sintaxe da função DISTRBINOM tem os seguintes argumentos:
-
Núm_s Obrigatório. É o número de tentativas bem sucedidas.
-
Tentativas Obrigatório. É o número de tentativas independentes.
-
Probabilidade_s Obrigatório. É a probabilidade de sucesso em cada tentativa.
-
Cumulativo obrigatório. É um valor lógico que determina a forma da função. Se cumulativo for VERDADEIRO, DISTRBINOM devolve a função de distribuição cumulativa, que é a probabilidade de que existam no máximo núm_s sucessos; se for FALSO, devolve a função de densidade de probabilidade, que é a probabilidade de existirem núm_s sucessos.
Observações
-
Núm_s e tentativas são truncados para números inteiros.
-
Se number_s, tentativas ou probability_s não forem numéricos, DIST.BINOM devolve o #VALUE! #VALOR!
-
Se number_s < 0 ou number_s > avaliações, DIST.BINOM devolve o #NUM! #VALOR!
-
Se probability_s < 0 ou probability_s > 1, DIST.BINOM devolve o #NUM! #VALOR!
-
Se x = núm_s, n = tentativas e p = probabilidade_s, então a função de densidade de probabilidade binomial é:
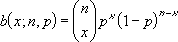
em que:

é COMBIN(n;x).
-
Se x = núm_s, n = tentativas e p = probabilidade_s, então a distribuição binomial cumulativa é:
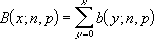
Exemplo
Copie os dados de exemplo na tabela seguinte e cole-os na célula A1 de uma nova folha de cálculo do Excel. Para que as fórmulas mostrem resultados, selecione-as, prima F2 e, em seguida, prima Enter. Se pretender, pode ajustar as larguras das colunas para ver todos os dados.
|
Dados |
Descrição |
|
|
6 |
Número de tentativas bem-sucedidas |
|
|
10 |
Número de tentativas independentes |
|
|
0,5 |
Probabilidade de sucesso em cada tentativa |
|
|
Fórmula |
Descrição |
Resultado |
|
=DISTRBINOM(A2;A3;A4;FALSO) |
Probabilidade de ter exatamente de 6 a 10 tentativas bem-sucedidas. |
0,2050781 |










