Returns the individual term binomial distribution probability. Use BINOMDIST in problems with a fixed number of tests or trials, when the outcomes of any trial are only success or failure, when trials are independent, and when the probability of success is constant throughout the experiment. For example, BINOMDIST can calculate the probability that two of the next three babies born are male.
Important: This function has been replaced with one or more new functions that may provide improved accuracy and whose names better reflect their usage. Although this function is still available for backward compatibility, you should consider using the new functions from now on, because this function may not be available in future versions of Excel.
For more information about the new function, see BINOM.DIST function.
Syntax
BINOMDIST(number_s,trials,probability_s,cumulative)
The BINOMDIST function syntax has the following arguments:
-
Number_s Required. The number of successes in trials.
-
Trials Required. The number of independent trials.
-
Probability_s Required. The probability of success on each trial.
-
Cumulative Required. A logical value that determines the form of the function. If cumulative is TRUE, then BINOMDIST returns the cumulative distribution function, which is the probability that there are at most number_s successes; if FALSE, it returns the probability mass function, which is the probability that there are number_s successes.
Remarks
-
Number_s and trials are truncated to integers.
-
If number_s, trials, or probability_s is nonnumeric, BINOMDIST returns the #VALUE! error value.
-
If number_s < 0 or number_s > trials, BINOMDIST returns the #NUM! error value.
-
If probability_s < 0 or probability_s > 1, BINOMDIST returns the #NUM! error value.
-
If x = number_s, n = trials, and p = probability_s, then the binomial probability mass function is:
where:

is COMBIN(n,x).
-
If x = number_s, n = trials, and p = probability_s, then the cumulative binomial distribution is:
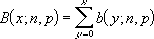
Example
Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.
|
Data |
Description |
|
|
6 |
Number of successes in trials |
|
|
10 |
Number of independent trials |
|
|
0.5 |
Probability of success on each trial |
|
|
Formula |
Description |
Result |
|
=BINOMDIST(A2,A3,A4,FALSE) |
Probability of exactly 6 of 10 trials being successful. |
0.2050781 |











