I denne artikel beskrives formelsyntaksen for og brugen af funktionen PEARSON i Microsoft Excel.
Beskrivelse
Returnerer Pearson's korrelationskoefficient, r, som er et dimensionsløst indeks, der går fra -1,0 til 1,0 begge inklusive, og som viser omfanget af et lineært forhold mellem to datasæt.
Syntaks
PEARSON(matrix1;matrix2)
Syntaksen for funktionen PEARSON har følgende argumenter:
-
Matrix1 Påkrævet. Et sæt af uafhængige værdier.
-
Matrix2 Påkrævet. Et sæt af afhængige værdier.
Bemærkninger
-
Argumenterne skal være tal eller navne, vektorkonstanter eller referencer, der indeholder tal.
-
Hvis et matrix- eller referenceargument indeholder tekst, logiske værdier eller tomme celler, ignoreres disse værdier, mens celler med værdien nul medtages.
-
Hvis vektor1 og vektor2 er tomme eller har forskellige antal datamærker, returnerer PEARSON fejlværdien #I/T.
-
Formlen for Pearson's korrelationskoefficient, r, er:
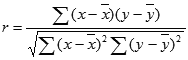
hvor x og y er stikprøvernes middelværdi MIDDEL(matrix1) og MIDDEL(matrix2).
Eksempel
Kopiér eksempeldataene i følgende tabel, og sæt dem ind i celle A1 i et nyt Excel-regneark. For at få formlerne til at vise resultater skal du markere dem, trykke på F2 og derefter trykke på Enter. Hvis der er brug for det, kan du justere bredden på kolonnerne, så du kan se alle dataene.
|
Data |
||
|
Uafhængige værdier |
Afhængige værdier |
|
|
9 |
10 |
|
|
7 |
6 |
|
|
5 |
1 |
|
|
3 |
5 |
|
|
1 |
3 |
|
|
Formel |
Beskrivelse (resultat) |
R esultat |
|
=PEARSON(A3:A7;B3:B7) |
Pearsons korrelationskoefficient for datasættene ovenfor (0,699379) |
0,699379 |










