In diesem Artikel werden die Formelsyntax und die Verwendung der Funktion PEARSON in Microsoft Excel beschrieben.
Beschreibung
Gibt den Pearsonschen Korrelationskoeffizienten r zurück. Dieser Koeffizient ist ein dimensionsloser Index mit dem Wertebereich -1,0 ≤ r ≤ 1,0 und ein Maß dafür, inwieweit zwischen zwei Datensätzen eine lineare Abhängigkeit besteht.
Syntax
PEARSON(Matrix1;Matrix2)
Die Syntax der Funktion PEARSON weist die folgenden Argumente auf:
-
Matrix1 Erforderlich. Eine Reihe unabhängiger Werte
-
Matrix2 Erforderlich. Eine Reihe abhängiger Werte
Hinweise
-
Als Argumente müssen entweder Zahlen oder Namen, Matrizen oder Bezüge angegeben werden, die Zahlen enthalten.
-
Enthält ein als Matrix oder Bezug angegebenes Argument Text, Wahrheitswerte oder leere Zellen, werden diese Werte ignoriert. Zellen, die den Wert 0 enthalten, werden dagegen berücksichtigt.
-
Enthalten Matrix1 und Matrix2 keine oder unterschiedlich viele Datenpunkte, gibt PEARSON den Fehlerwert #NV zurück.
-
Die Formel für den Pearsonschen Korrelationskoeffizienten r lautet:
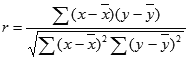
Dabei sind x und y die Stichprobenmittelwerte MITTELWERT(Array1) und MITTELWERT(Array2).
Beispiel
Kopieren Sie die Beispieldaten in der folgenden Tabelle, und fügen Sie sie in Zelle A1 eines neuen Excel-Arbeitsblatts ein. Um die Ergebnisse der Formeln anzuzeigen, markieren Sie sie, drücken Sie F2 und dann die EINGABETASTE. Im Bedarfsfall können Sie die Breite der Spalten anpassen, damit alle Daten angezeigt werden.
|
Daten |
||
|
Unabhängige Werte |
Abhängige Werte |
|
|
9 |
10 |
|
|
7 |
6 |
|
|
5 |
1 |
|
|
3 |
5 |
|
|
1 |
3 |
|
|
Formel |
Beschreibung (Ergebnis) |
Ergebnis |
|
=PEARSON(A3:A7;B3:B7) |
Der Pearsonsche Korrelationskoeffizient (Produkt-Moment-Korrelation) für die angegebenen Datenmengen (0,699379) |
0,699379 |










