This article describes the formula syntax and usage of the PEARSON function in Microsoft Excel.
Description
Returns the Pearson product moment correlation coefficient, r, a dimensionless index that ranges from -1.0 to 1.0 inclusive and reflects the extent of a linear relationship between two data sets.
Syntax
PEARSON(array1, array2)
The PEARSON function syntax has the following arguments:
-
Array1 Required. A set of independent values.
-
Array2 Required. A set of dependent values.
Remarks
-
The arguments must be either numbers or names, array constants, or references that contain numbers.
-
If an array or reference argument contains text, logical values, or empty cells, those values are ignored; however, cells with the value zero are included.
-
If array1 and array2 are empty or have a different number of data points, PEARSON returns the #N/A error value.
-
The formula for the Pearson product moment correlation coefficient, r, is:
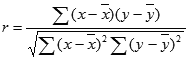
where x and y are the sample means AVERAGE(array1) and AVERAGE(array2).
Example
Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.
|
Data |
||
|
Independent values |
Dependent values |
|
|
9 |
10 |
|
|
7 |
6 |
|
|
5 |
1 |
|
|
3 |
5 |
|
|
1 |
3 |
|
|
Formula |
Description (Result) |
R esult |
|
=PEARSON(A3:A7,B3:B7) |
Pearson product moment correlation coefficient for the data sets above (0.699379) |
0.699379 |










