This article describes the formula syntax and usage of the SLOPE function in Microsoft Excel.
Description
Returns the slope of the linear regression line through data points in known_y's and known_x's. The slope is the vertical distance divided by the horizontal distance between any two points on the line, which is the rate of change along the regression line.
Syntax
SLOPE(known_y's, known_x's)
The SLOPE function syntax has the following arguments:
-
Known_y's Required. An array or cell range of numeric dependent data points.
-
Known_x's Required. The set of independent data points.
Remarks
-
The arguments must be either numbers or names, arrays, or references that contain numbers.
-
If an array or reference argument contains text, logical values, or empty cells, those values are ignored; however, cells with the value zero are included.
-
If known_y's and known_x's are empty or have a different number of data points, SLOPE returns the #N/A error value.
-
The equation for the slope of the regression line is:
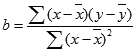
where x and y are the sample means AVERAGE(known_x’s) and AVERAGE(known_y’s).
-
The underlying algorithm used in the SLOPE and INTERCEPT functions is different than the underlying algorithm used in the LINEST function. The difference between these algorithms can lead to different results when data is undetermined and collinear. For example, if the data points of the known_y's argument are 0 and the data points of the known_x's argument are 1:
-
SLOPE and INTERCEPT return a #DIV/0! error. The SLOPE and INTERCEPT algorithm is designed to look for one and only one answer, and in this case there can be more than one answer.
-
LINEST returns a value of 0. The LINEST algorithm is designed to return reasonable results for collinear data, and in this case at least one answer can be found.
-
Example
Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.
|
Data |
||
|---|---|---|
|
Known y |
Known x |
|
|
1/2/1900 |
6 |
|
|
1/3/1900 |
5 |
|
|
1/9/1900 |
11 |
|
|
1/1/1900 |
7 |
|
|
1/8/1900 |
5 |
|
|
1/7/1900 |
4 |
|
|
1/5/1900 |
4 |
|
|
Formula |
Description |
Result |
|
=SLOPE(A3:A9,B3:B9) |
Slope of the linear regression line through the data points in A3:A9 and B3:B9. |
0.305556 |