The TREND function returns values along a linear trend. It fits a straight line (using the method of least squares) to the array's known_y's and known_x's. TREND returns the y-values along that line for the array of new_x's that you specify.
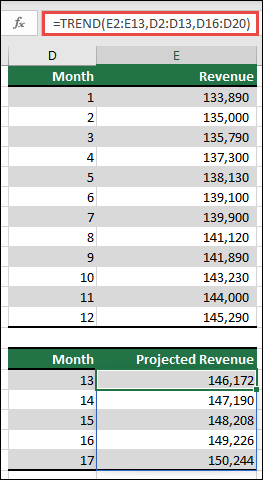
Note: If you have a current version of Microsoft 365, then you can input the formula in the top-left-cell of the output range (cell E16 in this example), then press ENTER to confirm the formula as a dynamic array formula. Otherwise, the formula must be entered as a legacy array formula by first selecting the output range (E16:E20), input the formula in the top-left-cell of the output range (E16), then press CTRL+SHIFT+ENTER to confirm it. Excel inserts curly brackets at the beginning and end of the formula for you. For more information on array formulas, see Guidelines and examples of array formulas.
=TREND(known_y's, [known_x's], [new_x's], [const])
The TREND function syntax has the following arguments:
|
Argument |
Description |
|---|---|
|
known_y's Required |
The set of y-values you already know in the relationship y = mx + b
|
|
known_x's Optional |
An optional set of x-values that you may already know in the relationship y = mx + b
|
|
new_x's Optional |
New x-values for which you want TREND to return corresponding y-values
|
|
const Optional |
A logical value specifying whether to force the constant b to equal 0
|
-
For information about how Microsoft Excel fits a line to data, see LINEST.
-
You can use TREND for polynomial curve fitting by regressing against the same variable raised to different powers. For example, suppose column A contains y-values and column B contains x-values. You can enter x^2 in column C, x^3 in column D, and so on, and then regress columns B through D against column A.
-
Formulas that return arrays must be entered as array formulas with Ctrl+Shift+Enter, unless you have a current version of Microsoft 365, and then you can just press Enter.
-
When entering an array constant for an argument such as known_x's, use commas to separate values in the same row and semicolons to separate rows.
Need more help?
You can always ask an expert in the Excel Tech Community or get support in Communities.










