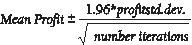Tento článek byl upraven z článku Analýza dat a obchodní modelování v Microsoft Excelu wayne L. Winston.
-
Kdo používá simulaci Monte Carlo?
-
Co se stane, když do buňky zadáte =RAND( )?
-
Jak můžete simulovat hodnoty diskrétní náhodné proměnné?
-
Jak můžete simulovat hodnoty normální náhodné proměnné?
-
Jak může společnost s přáními určit, kolik karet se má vyrobit?
Rádi bychom přesně odhadli pravděpodobnosti nejistých událostí. Jaká je například pravděpodobnost, že peněžní toky nového produktu budou mít kladnou čistou současnou hodnotu (ČISTÁ.SOUČHODNOTA)? Jaký je rizikový faktor našeho investičního portfolia? Simulace Monte Carlo nám umožňuje modelovat situace, které představují nejistotu, a pak si je tisíckrát přehrát na počítači.
Poznámka: Název Simulace Monte Carlo pochází z počítačových simulací provedených během 30. a 40. let, aby se odhadla pravděpodobnost, že řetězová reakce potřebná k odpálení atomové bomby bude fungovat úspěšně. Fyzikové zapojeni do této práce byli velcí fanoušci hazardních her, takže dali simulaci kódové jméno Monte Carlo.
V dalších pěti kapitolách uvidíte příklady použití Excelu k provádění simulací Monte Carlo.
Mnoho společností používá simulaci Monte Carlo jako důležitou součást svého rozhodovacího procesu. Tady je několik příkladů.
-
General Motors, Proctor and Gamble, Pfizer, Bristol-Myers Squibb a Eli Lilly používají simulaci k odhadu průměrné návratnosti i rizikového faktoru nových produktů. Společnost GM používá tyto informace generální ředitel k určení, které produkty přicházejí na trh.
-
Gm používá simulaci pro činnosti, jako je prognóza čistého příjmu pro společnost, predikce strukturálních a nákupních nákladů a určení její citlivosti k různým druhům rizika (jako jsou změny úrokových sazeb a kolísání směnných kurzů).
-
Lilly používá simulaci k určení optimální kapacity rostliny pro každý lék.
-
Proctor a Gamble využívá simulaci k modelování a optimálnímu zajištění devizového rizika.
-
Společnost Sears pomocí simulace určuje, kolik jednotek každé produktové řady by mělo být objednáno od dodavatelů – například počet párů kalhot Dockers, které by měly být objednány v tomto roce.
-
Ropné a lékové společnosti používají simulaci k hodnotě "skutečných možností", jako je hodnota možnosti rozšířit, uzavřít smlouvu nebo odložit projekt.
-
Finanční plánovači používají simulaci Monte Carlo k určení optimálních investičních strategií pro odchod svých klientů do důchodu.
Když do buňky zadáte vzorec =RAND(), získáte číslo, u kterého je stejně pravděpodobné, že bude předpokládat libovolnou hodnotu mezi 0 a 1. To znamená, že přibližně 25 procent času byste měli získat číslo menší než nebo rovno 0,25; přibližně 10 procent času byste měli získat číslo, které je alespoň 0,90 atd. Abyste si ukázali, jak funkce NÁHČÍSLO funguje, podívejte se na soubor Randdemo.xlsx, jak je znázorněno na obrázku 60-1.
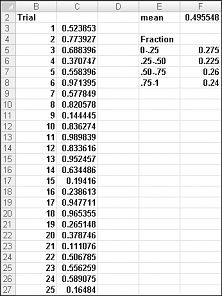
Poznámka: Když otevřete soubor Randdemo.xlsx, neuvidíte stejná náhodná čísla zobrazená na obrázku 60-1. Funkce NÁHČÍSLO vždy automaticky přepočítá čísla generovaná při otevření listu nebo při zadávání nových informací do listu.
Nejprve zkopírujte z buňky C3 do C4:C402 vzorec =RAND(). Pak oblast pojmenujete C3:C402 Data. Potom můžete ve sloupci F sledovat průměr 400 náhodných čísel (buňka F2) a pomocí funkce COUNTIF určit zlomky, které jsou mezi 0 a 0,25, 0,25 a 0,50, 0,50 a 0,75 a 0,75 a 0,75 a 1. Když stisknete klávesu F9, náhodná čísla se přepočítají. Všimněte si, že průměr 400 čísel je vždy přibližně 0,5 a že přibližně 25 procent výsledků je v intervalech 0,25. Tyto výsledky jsou konzistentní s definicí náhodného čísla. Všimněte si také, že hodnoty generované funkcí NÁHČÍSLO v různých buňkách jsou nezávislé. Pokud je například náhodné číslo vygenerované v buňce C3 velké číslo (například 0,99), nesděluje nám to nic o hodnotách ostatních vygenerovaných náhodných čísel.
Předpokládejme, že poptávka po kalendáři se řídí následující diskrétní náhodnou proměnnou:
|
Poptávka |
Pravděpodobnost: |
|---|---|
|
10 000 |
0,10 |
|
20 000 |
0.35 |
|
40,000 |
0,3 |
|
60 000 |
0,25 |
Jak můžeme excel mnohokrát přehrát nebo simulovat tuto poptávku po kalendářích? Trik spočívá v přidružení každé možné hodnoty funkce RAND s možnou poptávkou po kalendářích. Následující přiřazení zajistí, že požadavek 10 000 bude probíhat 10 procent času atd.
|
Poptávka |
Přiřazené náhodné číslo |
|---|---|
|
10 000 |
Méně než 0,10 |
|
20 000 |
Větší než nebo rovno 0,10 a menší než 0,45 |
|
40,000 |
Větší než nebo rovno 0,45 a menší než 0,75 |
|
60 000 |
Větší než nebo rovno 0,75 |
Pokud chcete předvést simulaci poptávky, podívejte se na soubor Discretesim.xlsx, který je znázorněn na obrázku 60-2 na další stránce.
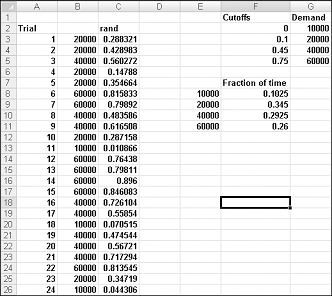
Klíčem k simulaci je použití náhodného čísla k zahájení vyhledávání z oblasti tabulky F2:G5 (pojmenované vyhledávání). Náhodná čísla větší nebo rovna 0 a menší než 0,10 budou vyžadovat 10 000; náhodná čísla větší nebo rovna 0,10 a menší než 0,45 budou vyžadovat 20 000; náhodná čísla větší nebo rovna 0,45 a menší než 0,75 budou vyžadovat 40 000; a náhodná čísla větší nebo rovna 0,75 vygeneruje požadavek 60 000. 400 náhodných čísel vygenerujete zkopírováním vzorce RAND() z C3 do C4:C402. Potom vygenerujete 400 zkušebních pokusů (iterací) poptávky kalendáře zkopírováním vzorce SVYHLEDAT(C3;vyhledávání;2) z B3 do B4:B402. Tento vzorec zajišťuje, že jakékoli náhodné číslo menší než 0,10 vygeneruje požadavek 10 000, jakékoli náhodné číslo mezi 0,10 a 0,45 vygeneruje požadavek 20 000 atd. V oblasti buněk F8:F11 pomocí funkce COUNTIF určete zlomek našich 400 iterací, které přinášejí každou poptávku. Když stiskneme klávesu F9 a přepočítáme náhodná čísla, simulované pravděpodobnosti se budou blížit předpokládané pravděpodobnosti poptávky.
Pokud do libovolné buňky zadáte vzorec NORMINV(rand(),mu,sigma), vygenerujete simulovanou hodnotu normální náhodné proměnné se střední hodnotou mu a směrodatnou odchylkou sigma. Tento postup je znázorněn na Normalsim.xlsx souboru, který je znázorněn na obrázku 60-3.
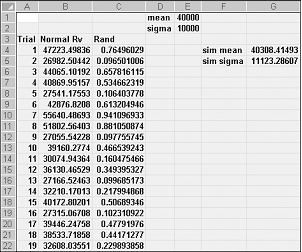
Předpokládejme, že chceme simulovat 400 pokusů nebo iterací pro normální náhodnou proměnnou se středníkem 40 000 a směrodatnou odchylkou 10 000. (Tyto hodnoty můžete zadat do buněk E1 a E2 a pojmenovat tyto buňky mean a sigma.) Zkopírováním vzorce =RAND() z C4 do C5:C403 se vygeneruje 400 různých náhodných čísel. Při kopírování z B4 do B5:B403 vzorec NORMINV(C4;střední;sigma) vygeneruje 400 různých hodnot pokusů z normální náhodné proměnné se střední hodnotou 40 000 a směrodatnou odchylkou 10 000. Když stiskneme klávesu F9 a přepočítáme náhodná čísla, zůstane průměr blízko 40 000 a směrodatná odchylka se blíží 10 000.
V podstatě pro náhodné číslo x vzorec NORMINV(p,mu,sigma) vygeneruje ptý percentil normální náhodné proměnné se střední mu a směrodatnou odchylkou sigma. Například náhodné číslo 0,77 v buňce C4 (viz obrázek 60-3) vygeneruje v buňce B4 přibližně 77. percentil normální náhodné proměnné se středníkem 40 000 a směrodatnou odchylkou 10 000.
V této části se dozvíte, jak lze simulaci Monte Carlo použít jako nástroj pro rozhodování. Předpokládejme, že poptávka po kartě Valentýna se řídí následující diskrétní náhodnou proměnnou:
|
Poptávka |
Pravděpodobnost: |
|---|---|
|
10 000 |
0,10 |
|
20 000 |
0.35 |
|
40,000 |
0,3 |
|
60 000 |
0,25 |
Přání se prodává za 4,00 USD a variabilní náklady na výrobu každé karty jsou 1,50 USD. Zbývající karty musí být zlikvidovány za cenu 0,20 USD za kartu. Kolik karet se má vytisknout?
V podstatě simulujeme každé možné množství výroby (10 000, 20 000, 40 000 nebo 60 000) mnohokrát (například 1 000 iterací). Pak určíme, které množství objednávek vynáší maximální průměrný zisk nad 1000 iterací. Data pro tento oddíl najdete v Valentine.xlsx souboru, jak je znázorněno na obrázku 60-4. Názvy oblastí v buňkách B1:B11 přiřadíte buňkám C1:C11. Oblast buněk G3:H6 má přiřazené vyhledávání názvů. Parametry prodejní ceny a nákladů jsou zadané v buňkách C4:C6.
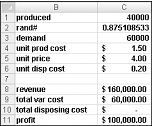
Do buňky C1 můžete zadat zkušební výrobní množství (v tomto příkladu 40 000). Dále vytvořte náhodné číslo v buňce C2 pomocí vzorce =RAND(). Jak jsme popsali dříve, simulujete poptávku po kartě v buňce C3 pomocí vzorce SVYHLEDAT(rand;vyhledávání;2). (Ve vzorci FUNKCE SVYHLEDAT je rand název buňky přiřazený buňce C3, ne funkce NÁHČÍSLO.)
Počet prodaných jednotek je menší z našeho výrobního množství a poptávky. V buňce C8 vypočítáte výnosy pomocí vzorce MIN(produkováno,poptávka)*unit_price. V buňce C9 vypočítáte celkové výrobní náklady pomocí vytvořeného vzorce*unit_prod_cost.
Pokud vyrobíme více karet, než je v poptávce, počet zbývajících jednotek se rovná výrobě minus poptávka; jinak nezůstaly žádné jednotky. Náklady na likvidaci vypočítáme v buňce C10 pomocí vzorce unit_disp_cost*KDYŽ (vyrobeno>poptávka,produkce–poptávka,0). Nakonec v buňce C11 vypočítáme zisk jako výnosy – total_var_cost-total_disposing_cost.
Chtěli bychom efektivní způsob, jak stisknout F9 mnohokrát (například 1000) pro každé množství výroby a sčítáme očekávaný zisk z každého množství. V této situaci nám přijde na pomoc obousměrná tabulka dat. (Podrobnosti o tabulkách dat najdete v kapitole 15 Analýza citlivosti s tabulkami dat.) Tabulka dat použitá v tomto příkladu je znázorněna na obrázku 60-5.

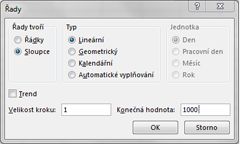
Do oblasti buněk A16:A1015 zadejte čísla 1–1000 (odpovídajících 1000 pokusům). Jedním ze snadných způsobů, jak tyto hodnoty vytvořit, je začít zadáním hodnoty 1 do buňky A16. Vyberte buňku a potom na kartě Domů ve skupině Úpravy klikněte na Vyplnit a výběrem řady zobrazte dialogové okno Řady . V dialogovém okně Řady , které je znázorněno na obrázku 60-6, zadejte hodnotu kroku 1 a hodnotu stop 1000. V oblasti Series V vyberte možnost Sloupce a potom klikněte na OK. Čísla 1–1000 budou zadána ve sloupci A počínaje buňkou A16.
Dále zadáme naše možná výrobní množství (10 000, 20 000, 40 000, 60 000) do buněk B15:E15. Chceme vypočítat zisk pro každé zkušební číslo (1 až 1000) a každé množství výroby. Vzorec pro zisk (vypočítaný v buňce C11) v levé horní buňce tabulky dat (A15) odkazujeme zadáním =C11.
Teď jsme připraveni oklamat Excel, aby simuloval 1000 iterací poptávky pro každé výrobní množství. Vyberte oblast tabulky (A15:E1014) a potom ve skupině Datové nástroje na kartě Data klikněte na What If Analysis (What If Analysis) a pak vyberte Data Table (Tabulka dat). Pokud chcete nastavit obousměrnou tabulku dat, zvolte jako vstupní buňku řádku naše výrobní množství (buňka C1) a jako vstupní buňku sloupce vyberte libovolnou prázdnou buňku (vybrali jsme buňku I14). Po kliknutí na OK excel simuluje 1000 hodnot poptávky pro každé množství objednávky.
Abyste pochopili, proč to funguje, vezměte v úvahu hodnoty umístěné v tabulce dat v oblasti buněk C16:C1015. Pro každou z těchto buněk použije Excel v buňce C1 hodnotu 20 000. V buňce C16 se hodnota vstupní buňky sloupce 1 umístí do prázdné buňky a náhodné číslo v buňce C2 se přepočítá. Odpovídající zisk se pak zaznamená do buňky C16. Potom se vstupní hodnota buňky sloupce 2 umístí do prázdné buňky a náhodné číslo v buňce C2 se znovu přepočítá. Odpovídající zisk se zadává do buňky C17.
Zkopírováním vzorce PRŮMĚR(B16:B1015) z buňky B13 do C13:E13 vypočítáme průměrný simulovaný zisk pro každé výrobní množství. Zkopírováním vzorce SMODCH.VÝBĚR(B16:B1015) z buňky B14 do C14:E14 vypočítáme směrodatnou odchylku simulovaných zisků pro každé množství objednávky. Při každém stisknutí klávesy F9 se pro každé množství objednávky simuluje 1 000 iterací poptávky. Při výrobě 40 000 karet se vždy dosáhne největšího očekávaného zisku. Proto se zdá, že vytvoření 40 000 karet je správné rozhodnutí.
Dopad rizika na naše rozhodnutí Pokud bychom místo 40 000 karet vygenerovali 20 000, náš očekávaný zisk klesne přibližně o 22 procent, ale naše riziko (měřené směrodatnou odchylkou zisku) klesne téměř o 73 procent. Proto, pokud jsme extrémně nechutný k riziku, může být vytvoření 20 000 karet správným rozhodnutím. Mimochodem, produkce 10 000 karet má vždy směrodatnou odchylku 0 karet, protože pokud vyrobíme 10 000 karet, vždy je prodáme všechny bez jakýchkoliv zbylých karet.
Poznámka: V tomto sešitu je možnost Výpočet nastavená na Automaticky s výjimkou tabulek. (Použijte příkaz Výpočet ve skupině Výpočet na kartě Vzorce.) Toto nastavení zajistí, že se tabulka dat nebude přepočítávat, dokud nestiskneme klávesu F9, což je dobrý nápad, protože velká tabulka dat zpomalí vaši práci, pokud přepočítává pokaždé, když něco zadáte do listu. Všimněte si, že v tomto příkladu se při každém stisknutí klávesy F9 změní průměrný zisk. K tomu dochází proto, že při každém stisknutí klávesy F9 se k vygenerování požadavků pro každé množství objednávky použije jiná posloupnost 1000 náhodných čísel.
Interval spolehlivosti pro střední zisk Přirozenou otázkou, kterou je třeba si v této situaci položit, je, do jakého intervalu jsme si na 95 procent jisti, že skutečný průměrný zisk klesne? Tento interval se označuje jako 95% interval spolehlivosti pro střední zisk. 95% interval spolehlivosti pro střední hodnotu výstupu simulace se vypočítá pomocí následujícího vzorce:
V buňce J11 vypočítáte dolní hranici 95% intervalu spolehlivosti průměrného zisku, když se vytvoří 40 000 kalendářů pomocí vzorce D13–1,96*D14/ODMOCNINA(1000). V buňce J12 vypočítáte horní limit pro náš 95% interval spolehlivosti pomocí vzorce D13+1,96*D14/ODMOCNINA(1000). Tyto výpočty jsou znázorněny na obrázku 60-7.

Jsme si z 95 procent jisti, že náš průměrný zisk, když je objednáno 40 000 kalendářů, je mezi 56 687 a 62 589 USD.
-
Prodejce GMC se domnívá, že poptávka po envoys v roce 2005 bude normálně rozdělena s průměrem 200 a směrodatnou odchylkou 30. Jeho náklady na přijetí vyslance jsou 25 000 dolarů a on prodá envo za 40 000 dolarů. Polovina všech envoů, kteří nejsou prodáni za plnou cenu, se dá prodat za 30 000 dolarů. Uvažuje o objednání 200, 220, 240, 260, 280 nebo 300 vyslanců. Kolik jich si má objednat?
-
Malý supermarket se snaží určit, kolik kopií Lidé časopis by si měli objednat každý týden. Věří, že se jejich poptávka po Lidé řídí následující diskrétní náhodnou proměnnou:
Poptávka
Pravděpodobnost:
15
0,10
20
0.20
25
0.30
30
0,25
35
0,15
-
Supermarket zaplatí 1,00 USD za každou kopii Lidé a prodá ji za 1,95 USD. Každá neprodaná kopie může být vrácena za 0,50 USD. Kolik kopií Lidé by mělo být v objednávce?
Potřebujete další pomoc?
Kdykoli se můžete zeptat odborníka z komunity Excel Tech nebo získat podporu v komunitách.