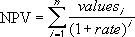ČISTÁ.SOUČHODNOTA (funkce)

Syntaxe

ČISTÁ.SOUČHODNOTA(sazba;hodnota1;hodnota2;...)

Sazba:     je sazba slevy za délku jednoho období.

Hodnota1, hodnota2,...     představuje 1 až 29 argumentů představujících platby a příjmy. Hodnota1, hodnota2,... musí být rovnoměrně rozmístěné v čase a na konci každého období. ČISTÁ.SOUČHODNOTA používá pořadí hodnot1, hodnota2,... k interpretaci pořadí peněžních toků. Zadávejte proto platby a příjmy ve správném pořadí. Argumenty, které jsou čísla, prázdné, logické hodnoty, nebo textové reprezentace čísel jsou počítány; Argumenty, které jsou chybovými hodnotami nebo texty, které nelze přeložit na čísla, jsou ignorovány.

Poznámky:

• Investice je realizována jedno období před datem prvního peněžního toku daného argumentem hodnota1 a končí posledním peněžním tokem v seznamu. Výpočet funkce ČISTÁ.SOUČHODNOTA je založen na budoucích peněžních tocích. Je-li první peněžní tok realizován na počátku prvního období, musí být tato hodnota k získanému výsledku přičtena a nesmí se udávat v seznamu hodnot. Další informace získáte v níže uvedeném příkladu.

• Máte-li n peněžních toků v seznamu hodnot, vzorec pro funkci ČISTÁ.SOUČHODNOTA je následující:

  

• ČISTÁ.SOUČHODNOTA je podobná funkci PV (současná hodnota). Primární rozdíl mezi PV a ČISTÁ.SOUČHODNOTA spočívá v tom, že pv umožňuje peněžní toky začínat na konci nebo na začátku období. Na rozdíl od proměnné ČISTÁ.SOUČHODNOTA peněžních toků musí být peněžní toky pv konstantní po celou dobu investice. Informace o anuitách a finančních funkcích najdete v tématu PV.

Příklad 1

V následujícím příkladu:

• Sazba je roční diskontní sazba.

• Hodnota1 je počáteční náklady na investici jeden rok od dnešního dne.

• Hodnota2 je výnos z prvního roku.

• Hodnota3 je návrat z druhého roku.

• Hodnota 4 je výnos třetího roku.

V příkladu zahrnete jako jednu z hodnot počáteční náklady 10 000 USD, protože platba proběhne na konci prvního období.

Příklad 2

V následujícím příkladu:

• Sazba je roční diskontní sazba. Může představovat míru inflace nebo úrokovou míru z alternativní investice.

• Hodnota1 je počáteční náklady na investici jeden rok od dnešního dne.

• Hodnota2 je výnos z prvního roku.

• Hodnota3 je návrat z druhého roku.

• Hodnota 4 je výnos třetího roku.

• Hodnota5 je návrat ze čtvrtého roku.

• Hodnota6 je návrat z pátého roku.

V příkladu nezahrnete jako jednu z hodnot počáteční náklady 40 000 USD, protože platba probíhá na začátku prvního období.