Vráti hodnotu binomického rozdělení pravděpodobnosti jednotlivých veličin. Funkci BINOM.DIST lze použít u problémů s pevným počtem testů nebo pokusů, kdy výsledek každého pokusu je pouze úspěch nebo neúspěch, pokusy jsou nezávislé a pravděpodobnost úspěchu během experimentu je konstantní. Pomocí funkce BINOM.DIST můžete například vypočítat pravděpodobnost, že dvě z dalších tří narozených dětí budou chlapci.
Syntaxe
BINOM.DIST(počet_úspěchů,pokusy,pravděpodobnost_úspěchu,kumulativní)
Syntaxe funkce BINOM.DIST má následující argumenty:
-
Počet_úspěchů: Povinný argument. Počet úspěšných pokusů.
-
Pokusy: Povinný argument. Počet nezávislých pokusů.
-
Pravděpodobnost_úspěchu: Povinný argument. Pravděpodobnost každého úspěšného pokusu.
-
Kumulativní: Povinný argument. Logická hodnota, která určuje typ použité funkce. Pokud je kumulativní hodnota PRAVDA, pak binom. Funkce DIST vrátí kumulativní distribuční funkci, což je pravděpodobnost, že je number_s úspěchů. pokud JE NEPRAVDA, vrátí pravděpodobnostní hromadnou funkci, což je pravděpodobnost, že number_s úspěchů.
Poznámky
-
Argumenty počet_úspěchů a pokusy jsou zkráceny na celá čísla.
-
Pokud number_s, pokusy nebo probability_s nejsou číselného typu, binom. Funkce DIST vrátí hodnotu #VALUE! chybová hodnota.
-
Pokud number_s < 0 nebo number_s > pokusů, BINOM. Funkce DIST vrátí hodnotu #NUM! chybová hodnota.
-
Pokud probability_s < 0 nebo probability_s > 1, BINOM. Funkce DIST vrátí hodnotu #NUM! chybová hodnota.
-
Hromadná pravděpodobnostní funkce binomického rozdělení je:
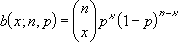
kde:
je KOMBINACE(n;x).
Kumulativní binomické rozdělení je:
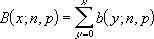
Příklad
Zkopírujte vzorová data v následující tabulce a vložte je do buňky A1 nového excelového sešitu. Aby vzorce zobrazily výsledky, vyberte je, stiskněte F2 a potom stiskněte Enter. Pokud potřebujete, můžete přizpůsobit šířky sloupců a zobrazit si všechna data.
|
Data |
Popis |
|
|
6 |
Počet úspěšných pokusů |
|
|
10 |
Počet nezávislých pokusů |
|
|
0,5 |
Pravděpodobnost úspěšného pokusu |
|
|
Vzorec |
Popis |
Výsledek |
|
=BINOM.DIST(A2;A3;A4;NEPRAVDA) |
Pravděpodobnost, že z 10 pokusů bude právě 6 úspěšných. |
0,2050781 |
