CONFIDENCE.NORM (funkce)

Popis

Interval spolehlivosti je oblast hodnot. Střední hodnotou vzorku x je střed této oblasti a oblast je x ± CONFIDENCE.NORM. Pokud je například x středním průměrem doby doručení produktů objednaných prostřednictvím pošty, x ± CONFIDENCE. NORM je oblast středních hodnot základního souboru. U všech středních hodnot základního souboru μ0 v tomto rozsahu je pravděpodobnost získání střední hodnoty vzorku dále od μ0 než x větší než alfa; u všech středních hodnot základního souboru, μ0, ne v tomto rozsahu, je pravděpodobnost získání střední hodnoty vzorku dále od μ0 než x menší než alfa. Jinými slovy, předpokládejme, že pomocí x, standard_dev a velikosti vytvoříme dvousekudový test na úrovni významnosti alfa hypotézy, že střední hodnota základního souboru je μ0. Pak tuto hypotézu neodmítneme, pokud je μ0 v intervalu spolehlivosti, a tuto hypotézu odmítne, pokud μ0 není v intervalu spolehlivosti. Interval spolehlivosti nám neumožňuje vyvozovat, že je pravděpodobnost 1 – alfa, že náš další balíček bude trvat dobu doručení, která je v intervalu spolehlivosti.

Syntaxe

CONFIDENCE.NORM(alfa,sm_odch,velikost)

Syntaxe funkce CONFIDENCE.NORM má následující argumenty:

• Alfa:     Povinný argument. Úroveň významnosti použitá k výpočtu úrovně spolehlivosti. Úroveň spolehlivosti se rovná 100*(1 - alfa)% nebo jinými slovy alfa 0,05 označuje úroveň spolehlivosti 95 procent.

• Sm_odch:     Povinný argument. Směrodatná odchylka základního souboru pro danou oblast dat a je pokládána za známou.

• Velikost:     Povinný argument. Velikost výběru.

Poznámky

• Pokud některý z argumentů není číselného typu, funkce CONFIDENCE. Funkce NORM vrátí hodnotu #VALUE! chybová hodnota.

• Pokud alfa ≤ 0 nebo alfa ≥ 1, spolehlivosti. Funkce NORM vrátí hodnotu #NUM! chybová hodnota.

• Pokud standard_dev ≤ 0, CONFIDENCE. Funkce NORM vrátí hodnotu #NUM! chybová hodnota.

• Pokud není argument velikost celé číslo, bude zkrácen.

• Pokud je < 1, spolehlivosti. Funkce NORM vrátí hodnotu #NUM! chybová hodnota.

• Za předpokladu, že se argument alfa rovná 0,05, je třeba vypočítat plochu pod křivkou standardního normálního rozdělení, která se rovná (1-alfa), neboli 95 %. Tato hodnota je ±1,96. Interval spolehlivosti je tedy:

  

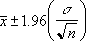
Příklad

Zkopírujte vzorová data v následující tabulce a vložte je do buňky A1 nového excelového sešitu. Aby vzorce zobrazily výsledky, vyberte je, stiskněte F2 a potom stiskněte Enter. Pokud potřebujete, můžete přizpůsobit šířky sloupců a zobrazit si všechna data.