Důležité informace: 14. října 2025 skončila podpora Office 2016 a Office 2019. Upgradujte na Microsoft 365, abyste mohli pracovat kdekoliv na libovolném zařízení a měli jste dál k dispozici podporu. Get Microsoft 365
Tento článek popisuje použití řešitele, což je doplněk microsoft excelového doplňku, který můžete použít pro citlivostní analýzu k určení optimální kombinace produktů.
Jak zjistím měsíční produktový mix, který maximalizuje ziskovost?
Společnosti často potřebují určit množství jednotlivých produktů, které se mají vyrábět, na měsíční bázi. Ve své nejjednodušší formě, produkt mix problém zahrnuje, jak určit množství každého produktu, který by měl být vyroben během měsíce, aby se maximalizovaly zisky. Produktová směs musí obvykle splňovat následující omezení:
-
Produktový mix nemůže používat více prostředků, než je k dispozici.
-
Poptávka po každém produktu je omezená. Během měsíce nemůžeme vyrobit více produktů, než vyžaduje poptávka, protože nadbytečná výroba je plýtvá (například lék podléhající zkáze).
Pojďme teď vyřešit následující příklad problému s kombinací produktů. Řešení tohoto problému najdete v Prodmix.xlsx souboru, který je znázorněn na obrázku 27-1.
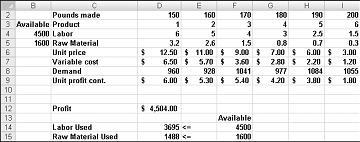
Řekněme, že pracujeme pro drogovou společnost, která vyrábí šest různých produktů ve své továrně. Výroba každého produktu vyžaduje práci a surovinu. Řádek 4 na obrázku 27-1 ukazuje hodiny práce potřebné k výrobě libry každého produktu a řádek 5 ukazuje libry suroviny potřebné k výrobě libry každého produktu. Například výroba libry produktu 1 vyžaduje šest hodin práce a 3,2 libry suroviny. U každého léku je cena za libru uvedena v řádku 6, jednotkové náklady na libru jsou uvedeny v řádku 7 a příspěvek na zisk na libru je uveden v řádku 9. Například Produkt 2 se prodává za 11,00 USD za libru, nese jednotkové náklady ve výši 5,70 USD za libru a přispívá ziskem 5,30 USD za libru. Měsíční poptávka po každém léku je uvedena v řádku 8. Například poptávka po produktu 3 je 1041 liber. Tento měsíc je k dispozici 4500 hodin práce a 1600 liber suroviny. Jak může tato společnost maximalizovat svůj měsíční zisk?
Kdybychom o Řešiteli v Excelu nic nevěděli, zaútočíme na tento problém vytvořením listu pro sledování zisku a využití prostředků spojených s produktovou kombinací. Pak bychom použili metodu pokusu a omylu k odličení produktové kombinace, abychom optimalizovali zisk bez použití většího množství práce nebo suroviny, než je k dispozici, a bez produkce jakéhokoliv léku nad poptávkou. Řešitele v tomto procesu používáme pouze ve fázi pokusu a omylu. Řešitel je v podstatě optimalizační modul, který bezvadně provádí hledání pokusů a chyb.
Klíčem k řešení problému s mixem produktů je efektivní výpočet využití prostředků a zisku spojeného s daným produktovým mixem. Důležitým nástrojem, který můžeme použít k provedení tohoto výpočtu, je funkce SOUČIN.SKALÁRNÍ. Funkce SOUČIN.SKALÁRNÍ vynásobí odpovídající hodnoty v oblastech buněk a vrátí součet těchto hodnot. Každá oblast buněk použitá při vyhodnocení SOUČIN.SKALÁRNÍ musí mít stejné rozměry, což znamená, že můžete použít SOUČIN.SKALÁRNÍ se dvěma řádky nebo dvěma sloupci, ale ne s jedním sloupcem a jedním řádkem.
Jako příklad použití funkce SOUČIN.SKALÁRNÍ v našem příkladu kombinace produktů zkusíme vypočítat využití prostředků. Naše využití práce se počítá podle
(Práce použitá na libru drogy 1)*(Lék 1 libra vyrobené)+ (Práce použitá na libru drogy 2)*(Drogy 2 libry vyrobené) + ... (Práce použitá na libru drogy 6)*(Drogy 6 liber vyrobené)
Využití práce bychom mohli vypočítat zdlouhavějším způsobem jako D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Podobně lze využití surovin vypočítat jako D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Zadání těchto vzorců do listu pro šest produktů je ale časově náročné. Představte si, jak dlouho by to trvalo, kdybyste spolupracovali se společností, která v jejich závodu vyrábí například 50 produktů. Mnohem jednodušší způsob, jak vypočítat využití práce a surovin, je zkopírovat vzorec z D14 do D15 SOUČIN.SKALÁRNÍ($D$2:$I$2;D4:I4). Tento vzorec vypočítá D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (což je naše pracovní využití), ale je mnohem jednodušší! Všimněte si, že používám znaménko $ s rozsahem D2:I2, takže při kopírování vzorce stále zachytávám produktový mix z řádku 2. Vzorec v buňce D15 vypočítá využití surovin.
Podobným způsobem je náš zisk určen
(Droga 1 zisk na libru)*(Lék 1 libra vyrobené) + (Droga 2 zisk na libru)*(Drogy 2 libra vyrobené) + ... (Droga 6 zisk na libru)*(Drogy 6 liber vyrobené)
Zisk se snadno vypočítá v buňce D12 pomocí vzorce SOUČIN.SKALÁRNÍ(D9:I9;$D$2:$I$2).
Teď můžeme identifikovat tři komponenty našeho modelu Řešitel na kombinaci produktů.
-
Cílová buňka. Naším cílem je maximalizovat zisk (vypočítaný v buňce D12).
-
Změna buněk. Počet liber vyrobených u každého produktu (uvedený v oblasti buněk D2:I2)
-
Omezení. Máme následující omezení:
-
Nepoužívejte více práce nebo suroviny, než je k dispozici. To znamená, že hodnoty v buňkách D14:D15 (použité prostředky) musí být menší nebo rovny hodnotám v buňkách F14:F15 (dostupné prostředky).
-
Nevyrábějte více léku, než je v poptávce. To znamená, že hodnoty v buňkách D2:I2 (libra produkované z každého léku) musí být menší nebo rovny poptávce po každém léku (uvedené v buňkách D8:I8).
-
Nemůžeme vyprodukovat záporné množství žádné drogy.
-
Ukážu vám, jak zadat cílovou buňku, změnit buňky a omezení do Řešitele. Pak stačí kliknout na tlačítko Vyřešit a najít produktový mix maximalizující zisk!
Začněte tak, že kliknete na kartu Data a ve skupině Analýza kliknete na Řešitel.
Poznámka: Jak je vysvětleno v kapitole 26, "Úvod do optimalizace pomocí Řešitele v Aplikaci Excel", řešitel se nainstaluje kliknutím na tlačítko Microsoft Office, potom na Možnosti aplikace Excel a potom na doplňky. V seznamu Spravovat klikněte na Doplňky aplikace Excel, zaškrtněte políčko Doplněk Řešitel a klikněte na OK.
Zobrazí se dialogové okno Parametry řešitele, jak je znázorněno na obrázku 27-2.
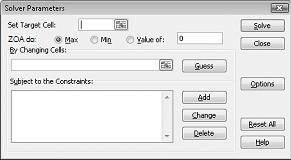
Klikněte na pole Nastavit cílovou buňku a vyberte buňku se ziskem (buňka D12). Klikněte na pole Podle změny buněk a pak přejděte na oblast D2:I2, která obsahuje libra produkovaná z každého léku. Dialogové okno by teď mělo vypadat jako Obrázek 27-3.
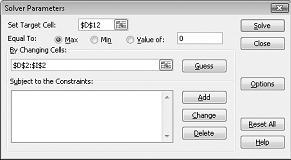
Teď jsme připraveni do modelu přidat omezení. Klikněte na tlačítko Přidat. Zobrazí se dialogové okno Přidat omezení, které je znázorněno na obrázku 27-4.
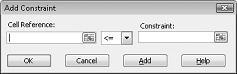
Pokud chcete přidat omezení využití prostředků, klikněte na pole Odkaz na buňku a vyberte oblast D14:D15. V prostředním seznamu vyberte <=. Klikněte na pole Omezení a vyberte oblast buněk F14:F15. Dialogové okno Přidat omezení by teď mělo vypadat jako Obrázek 27-5.
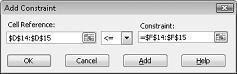
Teď jsme zajistili, že když Řešitel zkouší různé hodnoty pro měnící se buňky, budou se brát v úvahu pouze kombinace, které vyhovují oběma hodnotám D14<=F14 (využitá práce je menší nebo rovna dostupné práci) a D15<=F15 (použitá surovina je menší nebo rovna dostupné surovině). Kliknutím na Přidat zadejte omezení poptávky. Vyplňte dialogové okno Přidat omezení, jak je znázorněno na obrázku 27-6.
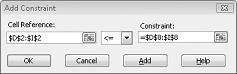
Přidáním těchto omezení zajistíte, že když Řešitel zkouší různé kombinace pro měnící se hodnoty buněk, budou se brát v úvahu pouze kombinace, které splňují následující parametry:
-
D2<=D8 (množství vyrobené lékem 1 je menší nebo se rovná poptávce po léku 1)
-
E2<=E8 (množství vyrobeného léku 2 je menší nebo rovno poptávce po léku 2)
-
F2<=F8 (množství vyrobené z léku 3 je menší nebo rovno poptávce po léku 3)
-
G2<=G8 (množství vyrobené z léku 4 je menší nebo se rovná poptávce po léku 4)
-
H2<=H8 (množství vyrobené z léku 5 je menší nebo se rovná poptávce po léku 5)
-
I2<=I8 (množství vyrobené z léku 6 je menší nebo se rovná poptávce po léku 6)
V dialogovém okně Přidat omezení klikněte na OK. Okno Řešitele by mělo vypadat jako Obrázek 27-7.
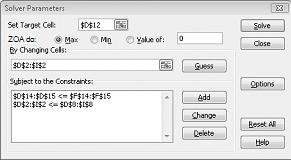
V dialogovém okně Možnosti řešitele zadáme omezení, že změna buněk musí být nezáporná. V dialogovém okně Parametry řešitele klikněte na tlačítko Možnosti. Zaškrtněte políčko Předpokládat lineární model a pole Předpokládat nezáporné, jak je znázorněno na obrázku 27-8 na další stránce. Klikněte na OK.
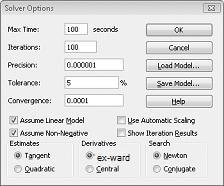
Zaškrtnutím políčka Předpokládat nezápornou hodnotu zajistíte, že Řešitel bere v úvahu pouze kombinace měnících se buněk, ve kterých každá změna buňky přebírá nezápornou hodnotu. Zaškrtnuli jsme políčko Předpokládat lineární model, protože problém kombinace produktů je speciálním typem problému Řešitele, kterému se říká lineární model. Model Řešitele je v podstatě lineární za následujících podmínek:
-
Cílová buňka se vypočítá sečtením termínů formuláře (změna buňky)*(konstanty).
-
Každé omezení splňuje požadavek na lineární model. To znamená, že každé omezení se vyhodnotí tak, že se sečtou termíny formuláře (změna buňky)*(konstanty) a porovná se součty s konstantou.
Proč je tento problém Řešitele lineární? Naše cílová buňka (zisk) se vypočítá jako
(Droga 1 zisk na libru)*(Lék 1 libra vyrobené) + (Droga 2 zisk na libru)*(Drogy 2 libra vyrobené) + ... (Droga 6 zisk na libru)*(Drogy 6 liber vyrobené)
Tento výpočet se řídí vzorem, ve kterém je hodnota cílové buňky odvozena součtem termínů formuláře (změna buňky)*(konstanta).
Naše pracovní omezení je vyhodnoceno porovnáním hodnoty odvozené od (Práce použitá na libru Drogy 1)*(Droga 1 libra vyrobené) + (Práce použitá na libru Drogy 2)*(Drogy 2 libra vyrobené)+ ... (Práce násed za libru Drogy 6)*(Drogy 6 liber vyrobené) na dostupnou práci.
Proto se pracovní omezení vyhodnotí tak, že se sečtou termíny formuláře (změna buňky)*(konstanty) a porovná se součty s konstantou. Pracovní i surovinové omezení splňují požadavek lineárního modelu.
Naše omezení poptávky mají podobu
(Lék 1 vyrobený)<=(Poptávka po 1 droze) (Lék 2 produkovaný)<=(Lék 2 Poptávka) §(Vyrobené drogy 6)<=(Poptávka po drogách 6)
Každé omezení poptávky také splňuje požadavek lineárního modelu, protože každé z nich se vyhodnocuje sečtením podmínek formuláře (změna buňky)*(konstanty) a porovnáním součtů s konstantou.
Když jsme ukázali, že náš model mixu produktů je lineární model, proč bychom se měli starat?
-
Pokud je model Řešitele lineární a vybereme Předpokládat lineární model, je zaručeno, že Řešitel najde optimální řešení pro model Řešitele. Pokud model Řešitele není lineární, řešitel může nebo nemusí najít optimální řešení.
-
Pokud je model Řešitele lineární a my vybereme Předpokládat lineární model, použije Řešitel k nalezení optimálního řešení modelu velmi efektivní algoritmus (metodu simplex). Pokud je model Řešitele lineární a nevybereme Možnost Předpokládat lineární model, použije Řešitel velmi neefektivní algoritmus (metodu GRG2) a může mít potíže s nalezením optimálního řešení modelu.
Po kliknutí na OK v dialogovém okně Možnosti řešitele se vrátíme do hlavního dialogového okna Řešitel, které je znázorněno dříve na obrázku 27-7. Když klikneme na Vyřešit, vypočítá Řešitel optimální řešení (pokud existuje) pro náš model mixu produktů. Jak jsem uvedl v kapitole 26, optimálním řešením modelu produktového mixu by byla sada měnících se hodnot buněk (libra vyrobené z každého léku), která maximalizuje zisk nad sadou všech proveditelných řešení. Znovu platí, že proveditelným řešením je sada měnících se hodnot buněk splňujících všechna omezení. Změny hodnot buněk znázorněné na obrázku 27-9 představují vhodné řešení, protože všechny úrovně výroby nejsou záporné, úrovně výroby nepřekračují poptávku a využití prostředků nepřekračuje dostupné prostředky.
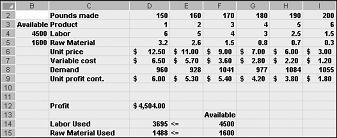
Měnící se hodnoty buněk zobrazené na obrázku 27-10 na další stránce představují neproveditelné řešení z následujících důvodů:
-
Vyrábíme více léku 5, než je poptávka po něm.
-
Používáme více práce, než je k dispozici.
-
Používáme více surovin, než je k dispozici.
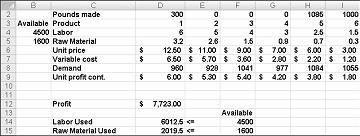
Po kliknutí na Vyřešit Řešit řešitel rychle najde optimální řešení znázorněné na obrázku 27-11. Pokud chcete zachovat optimální hodnoty řešení na listu, musíte vybrat Zachovat řešení Řešitele.
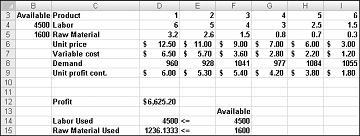
Naše drogová společnost může maximalizovat svůj měsíční zisk na úrovni $ 6,625.20 tím, že produkuje 596.67 liber Drogy 4, 1084 liber Drogy 5, a žádné z ostatních léků! Nemůžeme určit, jestli můžeme dosáhnout maximálního zisku 6 625,20 USD jinými způsoby. Můžeme si být jisti, že s našimi omezenými prostředky a poptávkou neexistuje způsob, jak tento měsíc vydělat více než 6 627,20 USD.
Předpokládejme, že poptávka po každém produktu musí být splněna. (Viz list Žádné možné řešení v souboru Prodmix.xlsx.) Pak musíme změnit omezení poptávky z D2:I2<=D8:I8 na D2:I2>=D8:I8. Uděláte to tak, že otevřete Řešitel, vyberete omezení D2:I2<=D8:I8 a potom kliknete na Změnit. Zobrazí se dialogové okno Změnit omezení, které je znázorněno na obrázku 27-12.
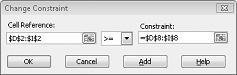
Vyberte >= a potom klikněte na OK. Teď jsme zajistili, že Řešitel bude uvažovat o změně pouze hodnot buněk, které splňují všechny požadavky. Když kliknete na Vyřešit, zobrazí se zpráva Řešitel nemohl najít proveditelné řešení. Tato zpráva neznamená, že jsme v našem modelu udělali chybu, ale spíše to, že s našimi omezenými prostředky nemůžeme uspokojit poptávku po všech produktech. Řešitel nám jednoduše říká, že pokud chceme uspokojit poptávku po každém produktu, musíme přidat více práce, více surovin nebo více obojího.
Podívejme se, co se stane, když povolíme neomezenou poptávku po každém produktu a umožníme, aby se z každého léku produkovala negativní množství. (Tento problém Řešitele můžete vidět na listu Nastavit hodnoty nekonvergovat v souboru Prodmix.xlsx.) Pokud chcete najít optimální řešení pro tuto situaci, otevřete Řešitel, klikněte na tlačítko Možnosti a zrušte zaškrtnutí políčka Předpokládat nezáporné. V dialogovém okně Parametry řešitele vyberte omezení poptávky D2:I2<=D8:I8 a kliknutím na Odstranit omezení odeberte. Když kliknete na Vyřešit, vrátí Řešitel zprávu "Nastavit hodnoty buněk se nekonvergují". Tato zpráva znamená, že pokud má být cílová buňka maximalizována (jako v našem příkladu), existují možná řešení s libovolně velkými hodnotami cílových buněk. (Pokud se má cílová buňka minimalizovat, znamená zpráva "Nastavit hodnoty buněk nekonverge" (Nastavit hodnoty buněk nesbližovat) vhodná řešení s libovolně malými hodnotami cílových buněk.) V naší situaci tím, že povolíme negativní produkci drogy, ve skutečnosti "vytváříme" zdroje, které mohou být použity k výrobě libovolně velkého množství jiných léků. Vzhledem k naší neomezené poptávce nám to umožňuje vytvářet neomezené zisky. V reálné situaci nemůžeme vydělat nekonečné množství peněz. Stručně řečeno, pokud se zobrazí "Nastavit hodnoty se nekonvergují", váš model obsahuje chybu.
-
Předpokládejme, že naše drogová společnost může koupit až 500 hodin práce za 1 dolar více, než jsou aktuální náklady na práci. Jak můžeme maximalizovat zisk?
-
V továrně na výrobu čipů vyrábí čtyři technici (A, B, C a D) tři produkty (Produkty 1, 2 a 3). Tento měsíc může výrobce čipu prodat 80 jednotek Produktu 1, 50 jednotek Produktu 2 a maximálně 50 jednotek Produktu 3. Technik A může vyrobit pouze produkty 1 a 3. Technik B může vyrobit pouze produkty 1 a 2. Technik C může vyrobit pouze produkt 3. Technik D může vyrobit pouze produkt 2. Za každou vyrobenou jednotku přispívají produkty následujícím ziskem: Produkt 1, 6 USD; Produkt 2, 7 Kč; a Produkt 3, 10 Kč. Doba (v hodinách), která každý technik potřebuje k výrobě produktu, je následující:
Produkt
Technik A
Technik B
Technik C
Technik D
1
2
2,5
Nejde to udělat
Nejde to udělat
2
Nejde to udělat
3
Nejde to udělat
3,5
3
3
Nejde to udělat
4
Nejde to udělat
-
Každý technik může pracovat až 120 hodin měsíčně. Jak může výrobce čipů maximalizovat svůj měsíční zisk? Předpokládejme, že lze vytvořit desetinný počet jednotek.
-
Počítačová továrna vyrábí myši, klávesnice a pákové ovladače videoher. Zisk na jednotku, využití práce na jednotku, měsíční poptávka a využití strojového času na jednotku jsou uvedeny v následující tabulce:
Myši
Klávesnice
Pákové ovladače
Profit/unit
1 000 Kč
11 Kč
99 Kč
Využití práce/ jednotka
0,2 hodina
.3 hodina
.24 hodina
Čas/jednotka stroje
0.04 hodina
0.055 hodina
0.04 hodina
Měsíční poptávka
15 000
27,000
11,000
-
Každý měsíc je k dispozici celkem 13 000 pracovních hodin a 3 000 hodin strojového času. Jak může výrobce maximalizovat svůj měsíční ziskový příspěvek ze závodu?
-
Vyřešte náš příklad léku za předpokladu, že musí být splněna minimální poptávka 200 jednotek pro každý lék.
-
Jason vyrábí diamantové náramky, náhrdelníky a náušnice. Chce pracovat maximálně 160 hodin měsíčně. Má 800 uncí diamantů. Zisk, pracovní doba a unce diamantů potřebných k výrobě každého produktu jsou uvedeny níže. Pokud je poptávka po každém produktu neomezená, jak může Jason maximalizovat svůj zisk?
Produkt
Jednotkové zisky
Pracovní doba na jednotku
Unce diamantů na jednotku
Náramek
300 Kč
.35
1,2
Náhrdelník
2 000 Kč
.15
.75
Náušnice
100 Kč
0,05
.5










