Denne artikel er tilpasset fra Microsoft Excel Data Analysis and Business Modeling af Wayne L. Winston.
-
Hvem bruger Monte Carlo-simulering?
-
Hvad sker der, når du skriver =SLUMP() i en celle?
-
Hvordan kan du simulere værdier af en diskret tilfældig variabel?
-
Hvordan kan du simulere værdier af en normal tilfældig variabel?
-
Hvordan kan en lykønskningskortvirksomhed bestemme, hvor mange kort der skal produceres?
Vi vil gerne nøjagtigt anslå sandsynlighederne for usikre begivenheder. Hvad er f.eks. sandsynligheden for, at pengestrømme for et nyt produkt har en positiv nettonutidsværdi (NUTIDSVÆRDI)? Hvad er risikofaktoren for vores investeringsportefølje? Monte Carlo simulering gør det muligt for os at modellere situationer, der giver usikkerhed, og derefter spille dem ud på en computer tusindvis af gange.
Bemærk!: Navnet Monte Carlo simulering kommer fra computersimuleringer udført i løbet af 1930'erne og 1940'erne for at vurdere sandsynligheden for, at kædereaktionen for en atombombe for at detonere ville fungere korrekt. Fysikerne involveret i dette arbejde var store fans af spil, så de gav simuleringer kodenavnet Monte Carlo.
I de næste fem kapitler vil du se eksempler på, hvordan du kan bruge Excel til at udføre Monte Carlo-simuleringer.
Mange virksomheder bruger Monte Carlo simulering som en vigtig del af deres beslutningsproces. Her er nogle eksempler.
-
General Motors, Proctor and Gamble, Pfizer, Bristol-Myers Squibb og Eli Lilly bruger simulering til at beregne både det gennemsnitlige afkast og risikofaktoren for nye produkter. Hos GM bruges disse oplysninger af den administrerende direktør til at bestemme, hvilke produkter der kommer på markedet.
-
GM bruger simulering til aktiviteter som f.eks. prognoser for virksomhedens nettoindtægt, forudsigelse af strukturelle omkostninger og indkøbsomkostninger og bestemmelse af dens modtagelighed for forskellige typer risici (f.eks. renteændringer og valutakursudsving).
-
Lilly bruger simulering til at bestemme den optimale anlægskapacitet for hvert stof.
-
Proctor og Gamble bruger simulering til at modellere og afdække valutarisiko optimalt.
-
Sears bruger simulering til at bestemme, hvor mange enheder af hver produktlinje der skal bestilles fra leverandører – f.eks. antallet af par Dockers bukser, der skal bestilles i år.
-
Olie- og medicinalvirksomheder bruger simulering til at værdsætte "reelle muligheder", f.eks. værdien af en mulighed for at udvide, indgå kontrakt eller udsætte et projekt.
-
Finansielle planlæggere bruger Monte Carlo-simulering til at bestemme optimale investeringsstrategier for deres kunders tilbagetrækning.
Når du skriver formlen =SLUMP() i en celle, får du et tal, der med lige stor sandsynlighed antager en værdi mellem 0 og 1. Således, omkring 25 procent af tiden, bør du få et tal mindre end eller lig med 0,25; omkring 10 procent af den tid, du skal få et tal, der er mindst 0,90, og så videre. For at vise, hvordan funktionen SLUMP fungerer, skal du se nærmere på filen Randdemo.xlsx, som vist i figur 60-1.
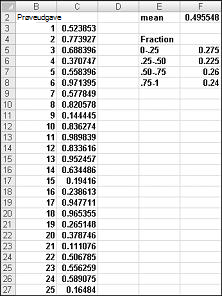
Bemærk!: Når du åbner filen Randdemo.xlsx, kan du ikke se de samme tilfældige tal, der er vist i Figur 60-1. Funktionen SLUMP genberegner altid automatisk de tal, den genererer, når et regneark åbnes, eller når der angives nye oplysninger i regnearket.
Først skal du kopiere formlen =SLUMP()fra celle C3 til C4:C402. Derefter skal du navngive området C3:C402 Data. Derefter kan du i kolonne F spore gennemsnittet af de 400 tilfældige tal (celle F2) og bruge funktionen TÆL.HVIS til at bestemme de brøker, der er mellem 0 og 0,25, 0,25 og 0,50, 0,50 og 0,75 og 0,75 og 1. Når du trykker på F9, genberegnes de tilfældige tal. Bemærk, at gennemsnittet af de 400 tal altid er ca. 0,5, og at omkring 25 procent af resultaterne er i intervaller på 0,25. Disse resultater er i overensstemmelse med definitionen af et tilfældigt tal. Bemærk også, at de værdier, der genereres af SLUMP i forskellige celler, er uafhængige. Hvis f.eks. det tilfældige tal, der genereres i celle C3, er et stort tal (f.eks. 0,99), fortæller det os intet om værdierne af de andre tilfældige tal, der genereres.
Antag, at behovet for en kalender er underlagt følgende diskrete tilfældige variabel:
|
Efterspørgsel |
Sandsynlighed |
|
10.000 |
0,10 |
|
20.000 |
0,35 |
|
40,000 |
0,3 |
|
60.000 |
0,25 |
Hvordan kan vi få Excel til at udspilne eller simulere denne efterspørgsel efter kalendere mange gange? Tricket er at knytte hver mulig værdi af funktionen SLUMP til et muligt behov for kalendere. Følgende opgave sikrer, at et behov på 10.000 vil forekomme 10 procent af tiden osv.
|
Efterspørgsel |
Tilfældigt nummer tildelt |
|
10.000 |
Mindre end 0,10 |
|
20.000 |
Større end eller lig med 0,10 og mindre end 0,45 |
|
40,000 |
Større end eller lig med 0,45 og mindre end 0,75 |
|
60.000 |
Større end eller lig med 0,75 |
For at demonstrere simuleringen af efterspørgsel skal du se på filen Discretesim.xlsx, der er vist i figur 60-2 på næste side.
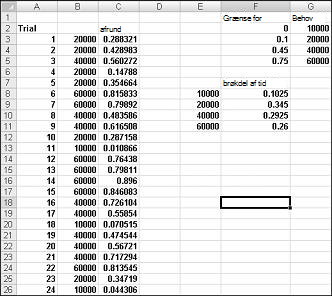
Nøglen til vores simulering er at bruge et tilfældigt tal til at starte et opslag fra tabelområdet F2:G5 (navngivet opslag). Tilfældige tal, der er større end eller lig med 0 og mindre end 0,10, giver et behov på 10.000. tilfældige tal, der er større end eller lig med 0,10 og mindre end 0,45, giver en efterspørgsel på 20.000. tilfældige tal, der er større end eller lig med 0,45 og mindre end 0,75, giver en efterspørgsel på 40.000. og tilfældige tal, der er større end eller lig med 0,75, giver en efterspørgsel på 60.000. Du genererer 400 tilfældige tal ved at kopiere formlen SLUMP()fra C3 til C4:C402. Derefter genererer du 400 prøveabonnementer eller gentagelser af kalenderbehov ved at kopiere formlen LOPSLAG(C3,opslag,2) fra B3 til B4:B402. Denne formel sikrer, at vilkårlige tal, der er mindre end 0,10, genererer et behov på 10.000, et vilkårligt tal mellem 0,10 og 0,45 genererer et behov på 20.000 osv. I celleområdet F8:F11 skal du bruge funktionen TÆL.HVIS til at bestemme brøkdelen af vores 400 gentagelser, der giver hvert behov. Når vi trykker på F9 for at genberegne de tilfældige tal, er de simulerede sandsynligheder tæt på vores formodede efterspørgsel sandsynligheder.
Hvis du skriver formlen NORMINV(slump(),mu,sigma) i en vilkårlig celle, genererer du en simuleret værdi af en tilfældig normal variabel, der har en middel mu - og standardafvigelse sigma. Denne fremgangsmåde er illustreret i filen Normalsim.xlsx, der er vist i figur 60-3.
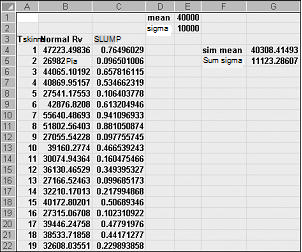
Lad os antage, at vi vil simulere 400 forsøg eller gentagelser for en normal tilfældig variabel med en middelværdi på 40.000 og en standardafvigelse på 10.000. Du kan skrive disse værdier i cellerne E1 og E2 og navngive henholdsvis middelværdien og sigmaet for disse celler. Kopiering af formlen =SLUMP() fra C4 til C5:C403 genererer 400 forskellige tilfældige tal. Når formlen NORMINV(C4,middelværdi,sigma) kopieres fra B4 til B5:B403, genereres der 400 forskellige prøveværdier fra en tilfældig normal variabel med en middelværdi på 40.000 og en standardafvigelse på 10.000. Når vi trykker på F9 for at genberegne de tilfældige tal, forbliver middelværdien tæt på 40.000, og standardafvigelsen er tæt på 10.000.
I bund og grund genererer formlen NORMINV(p,mu,sigma) for et tilfældigt tal x den p'tefraktil for en tilfældig normal variabel med en middelværdi mu og en standardafvigelse sigma. Det tilfældige tal 0,77 i celle C4 (se figur 60-3) genererer f.eks. i celle B4 omtrent den 77. fraktil for en tilfældig normal variabel med en middelværdi på 40.000 og en standardafvigelse på 10.000.
I dette afsnit kan du se, hvordan Monte Carlo-simulering kan bruges som et beslutningsværktøj. Antag, at efterspørgslen efter et Valentinsdagskort er underlagt følgende diskrete tilfældige variabel:
|
Efterspørgsel |
Sandsynlighed |
|
10.000 |
0,10 |
|
20.000 |
0,35 |
|
40,000 |
0,3 |
|
60.000 |
0,25 |
Kortet sælger for $ 4,00, og de variable omkostninger ved at producere hvert kort er $ 1,50. Resterende kort skal bortskaffes til en pris på $ 0,20 per kort. Hvor mange kort skal udskrives?
Dybest set simulerer vi hver mulig produktionsmængde (10.000, 20.000, 40.000 eller 60.000) mange gange (for eksempel 1000 gentagelser). Derefter bestemmer vi, hvilket ordreantal der giver det maksimale gennemsnitlige overskud i forhold til 1000 gentagelser. Du kan finde dataene for dette afsnit i filen Valentine.xlsx, der er vist i Figur 60-4. Du tildeler områdenavnene i cellerne B1:B11 til cellerne C1:C11. Celleområdet G3:H6 tildeles navneopslag. Vores salgspris- og omkostningsparametre angives i cellerne C4:C6.
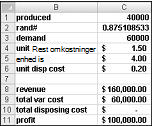
Du kan angive et prøveproduktionsantal (40.000 i dette eksempel) i celle C1. Derefter skal du oprette et tilfældigt tal i celle C2 med formlen =SLUMP(). Som tidligere beskrevet simulerer du behovet for kortet i celle C3 med formlen LOPSLAG(slump,opslag,2). (I LOPSLAG-formlen er slump det cellenavn, der er tildelt celle C3, ikke funktionen SLUMP).
Antallet af solgte enheder er den mindste af vores produktionsantal og -behov. I celle C8 beregner du vores indtægt med formlen MIN(produceret,efterspørgsel)*unit_price. I celle C9 skal du beregne de samlede produktionsomkostninger med den formel, der er produceret*unit_prod_cost.
Hvis vi producerer flere kort, end der er behov for, er antallet af enheder, der er tilbage, lig med produktionen minus efterspørgslen. ellers er der ingen enheder tilbage. Vi beregner vores bortskaffelsesomkostninger i celle C10 med formlen unit_disp_cost*HVIS(produceret>efterspørgsel,produceret –efterspørgsel,0). Endelig beregner vi i celle C11 vores overskud som indtægter – total_var_cost-total_disposing_cost.
Vi vil gerne have en effektiv metode til at trykke på F9 mange gange (f.eks. 1000) for hver produktionsmængde og optæller vores forventede overskud for hver mængde. Denne situation er en, hvor en to-vejs data tabel kommer til vores redning. (Se Kapitel 15, "Følsomhedsanalyse med datatabeller", hvis du vil have mere at vide om datatabeller. Den datatabel, der bruges i dette eksempel, vises i figur 60-5.
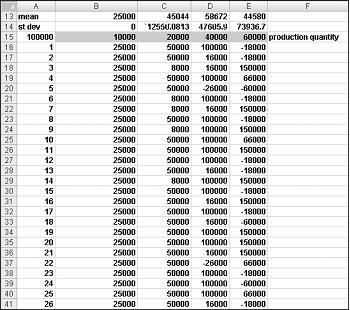
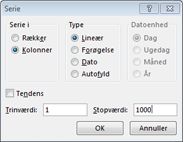
I celleområdet A16:A1015 skal du angive tallene 1-1000 (svarende til vores 1000 forsøg). En nem måde at oprette disse værdier på er at starte med at skrive 1 i celle A16. Markér cellen, og klik derefter på Fyld under fanen Hjem i gruppen Redigering, og vælg Serie for at få vist dialogboksen Serie. I dialogboksen Serie , der vises i Figur 60-6, skal du angive trinværdien 1 og stopværdien 1000. I området Serie i skal du vælge indstillingen Kolonner og derefter klikke på OK. Tallene 1-1000 angives i kolonne A startende i celle A16.
Dernæst angiver vi vores mulige produktionsmængder (10.000, 20.000, 40.000, 60.000) i cellerne B15:E15. Vi vil beregne overskuddet for hvert prøvenummer (1 til 1000) og hvert produktionsantal. Vi refererer til formlen for fortjeneste (beregnet i celle C11) i den øverste venstre celle i vores datatabel (A15) ved at skrive =C11.
Vi er nu klar til at narre Excel til at simulere 1000 gentagelser af efterspørgsel for hver produktionsmængde. Vælg tabelområdet (A15:E1014), og klik derefter på Hvad hvis-analyse i gruppen Dataværktøjer under fanen Data, og vælg derefter Datatabel. Hvis du vil konfigurere en tovejsdatatabel, skal du vælge vores produktionsantal (celle C1) som inputcelle for række og vælge en tom celle (vi valgte celle I14) som inputcelle for kolonne. Når du har klikket på OK, simulerer Excel 1000 behovsværdier for hvert ordreantal.
For at forstå, hvorfor dette fungerer, skal du overveje de værdier, der er placeret af datatabellen i celleområdet C16:C1015. For hver af disse celler bruger Excel en værdi på 20.000 i celle C1. I C16 placeres inputcelleværdien 1 for kolonnen i en tom celle, og det tilfældige tal i celle C2 genberegnes. Den tilsvarende fortjeneste registreres derefter i celle C16. Derefter placeres inputværdien for kolonnecellen på 2 i en tom celle, og det tilfældige tal i C2 genberegnes igen. Den tilsvarende fortjeneste angives i celle C17.
Ved at kopiere formlen MIDDEL(B16:B1015) fra celle B13 til C13:E13 beregner vi gennemsnitlig simuleret fortjeneste for hver produktionsmængde. Ved at kopiere formlen STDAFV(B16:B1015) fra celle B14 til C14:E14 beregner vi standardafvigelsen for vores simulerede overskud for hver ordremængde. Hver gang vi trykker på F9, simuleres 1000 gentagelser af behov for hver ordremængde. Produktion af 40.000 kort giver altid det største forventede overskud. Derfor ser det ud til, at produktion af 40.000 kort er den rette beslutning.
Risikoens indvirkning på vores beslutning Hvis vi producerede 20.000 i stedet for 40.000 kort, falder vores forventede overskud ca. 22 procent, men vores risiko (målt ved standardafvigelsen for profit) falder næsten 73 procent. Hvis vi derfor er ekstremt modvilligt til at risikere, kan det være den rigtige beslutning at producere 20.000 kort. I øvrigt producerer 10.000 kort altid en standardafvigelse på 0 kort, fordi hvis vi producerer 10.000 kort, vil vi altid sælge dem alle uden nogen rester.
Bemærk!: I denne projektmappe er indstillingen Beregning angivet til Automatisk undtagen tabeller. Brug kommandoen Beregning i gruppen Beregning under fanen Formler. Denne indstilling sikrer, at vores datatabel ikke genberegnes, medmindre vi trykker på F9, hvilket er en god ide, fordi en stor datatabel vil gøre arbejdet langsommere, hvis det genberegnes, hver gang du skriver noget i dit regneark. Bemærk, at når du i dette eksempel trykker på F9, ændres den gennemsnitlige fortjeneste. Dette sker, fordi hver gang du trykker på F9, bruges der en anden sekvens på 1000 tilfældige tal til at generere krav for hvert ordreantal.
Konfidensinterval for middelværdifortjeneste Et naturligt spørgsmål at stille i denne situation er, i hvilket interval er vi 95 procent sikker på den sande gennemsnitlige overskud vil falde? Dette interval kaldes konfidensintervallet på 95 % for den gennemsnitlige fortjeneste. Et konfidensinterval på 95 % for middelværdien af et simuleringsoutput beregnes med følgende formel:
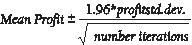
I celle J11 skal du beregne den nedre grænse for konfidensintervallet på 95 % for middeloverskud, når 40.000 kalendere fremstilles med formlen D13-1,96*D14/KVROD(1000). I celle J12 beregner du den øvre grænse for vores konfidensinterval på 95 % med formlen D13+1,96*D14/KVROD(1000). Disse beregninger er vist i figur 60-7.
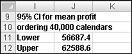
Vi er 95 procent sikre på, at vores gennemsnitlige overskud, når 40.000 kalendere er bestilt, er mellem $ 56.687 og $ 62.589.
-
En GMC forhandler mener, at efterspørgslen efter 2005 Envoys vil normalt blive fordelt med et gennemsnit på 200 og standardafvigelse på 30. Hans omkostninger ved at modtage en udsending er $ 25.000, og han sælger en udsending for $ 40.000. Halvdelen af alle udsendinge ikke sælges til fuld pris kan sælges for $ 30.000. Han overvejer at bestille 200, 220, 240, 260, 280 eller 300 udsendinge. Hvor mange skal han bestille?
-
Et lille supermarked forsøger at afgøre, hvor mange kopier af Mennesker magasin de skal bestille hver uge. De mener, at deres krav om Mennesker er underlagt følgende diskrete tilfældige variabel:
Efterspørgsel
Sandsynlighed
15
0,10
20
0.20
25
0.30
30
0,25
35
0,15
-
Supermarkedet betaler $ 1,00 for hver kopi af Mennesker og sælger det for $ 1,95. Hver usoldt kopi kan returneres for $ 0,50. Hvor mange kopier af Mennesker skal butiksordren have?
Har du brug for mere hjælp?
Du kan altid spørge en ekspert i Excel Tech Community eller få support i community'er.










