LINEST function

Beskrivelse

Funktionen LINREGR beregner en linjes stikprøvefunktioner ved at bruge de mindste kvadraters metode til beregning af den lige linje med den bedste tilnærmelse til dataene, og returnerer derefter en matrix, der beskriver linjen. Du kan også kombinere funktionen LINREGR med andre funktioner for at beregne statistikken for andre typer modeller, der er lineære, i de ukendte parametre, herunder polynomiske, logaritmiske og eksponentielle serier og potensserier. Da denne funktion returnerer en matrix med værdier, skal den angives som en matrixformel. Vejledningen følger eksemplerne i denne artikel.

Ligningen for linjen er:

y = mx + b

– eller –

y = m1x1 + m2x2 + ... + b

Hvis der er flere intervaller for x-værdier, hvor de afhængige y-værdier er en funktion af de uafhængige x-værdier. M-værdierne er koefficienter svarende til hver x-værdi, og b er en konstant værdi. Bemærk, at y, x og m kan være matrixer. Den matrix, funktionen LINREGR returnerer, er {mn;mn-1;...;m1;b}. LINREGR kan også returnere andre regressionsspecifikke stikprøvefunktioner.

Syntaks

LINREGR(kendte_y'er;[kendte_x'er];[konstant];[statistik])

Syntaksen for funktionen LINREGR har følgende argumenter:

Syntaks

• kendte_y'er Påkrævet. Det sæt y-værdier, som du eventuelt allerede kender fra forholdet y = mx + b.

  • Hvis området med kendte_y'er findes i en enkelt kolonne, fortolkes hver kolonne med kendte_x'er som en separat variabel.

  • Hvis området med kendte_y'er er placeret i en enkelt række, fortolkes hver række med kendte_x'er som en separat variabel.

• kendte_x'er Valgfrit. Et sæt x-værdier, som du eventuelt allerede kender fra forholdet y = mx + b.

  • Området med known_x kan omfatte et eller flere sæt variabler. Hvis der kun anvendes én variabel, known_y alle variabler og known_x'er kan være områder af en hvilken som helst figur, så længe de har samme dimensioner. Hvis der anvendes mere end én variabel, known_y en vektor (det vil sige et område med en højde på én række eller en bredde på én kolonne).

  • Hvis kendte_x'er udelades, antages matrixen {1;2;3;...}, der har samme størrelse som kendte_y'er.

• konstant Valgfrit. En logisk værdi, der angiver, om konstanten b skal være lig med 0.

  • Hvis konstant er SAND eller udelades, beregnes b på normal vis.

  • Hvis konstant er FALSK, defineres b som lig med 0, og m-værdierne justeres til y = mx.

• statistik Valgfrit. En logisk værdi, der angiver, om der skal returneres regressionsspecifikke stikprøvefunktioner.

  • Hvis statistik er SAND, returnerer LINEST de andre regressionsstatistik. som resultat er den returnerede matrix {mn;mn-1,...,m1;b;sen;sen-1,...,se1;seb;r²;sey; F,fg;ssreg,ssresid}.

  • Hvis statistik er FALSK eller udelades, returnerer LINREGR kun m-koefficienterne og konstanten b.

    De andre regressionsspecifikke stikprøvefunktioner er som følger:

I følgende illustration vises rækkefølgen, hvori de andre regressionsspecifikke stikprøvefunktioner returneres:

Bemærkninger

• Du kan beskrive en vilkårlig ret linje med hældningskoefficienten og y-skæringspunktet:

  Hældning (m):
  Hvis du vil finde hældningen for en linje, der ofte skrives som m, skal du tage to punkter på linjen (x1,y1) og (x2,y2); hældningen er lig med (y2 - y1)/(x2 - x1).

  Y-skæringspunkt (b):
  Y-skæringspunktet for en linje, der ofte skrives som b, er værdien af y på det punkt, hvor linjen krydser y-aksen.

  Ligningen for en ret linje er y = mx + b. Når du kender værdien af m og b, kan du beregne et vilkårligt punkt på linjen ved at indsætte y- eller x-værdien i ligningen. Du kan også bruge funktionen TENDENS.

• Når der kun er én uafhængig x-variabel, kan du udregne hældningskoefficienten og værdien for y-skæringspunktet direkte med følgende formler:

  Hældning:
  =INDEKS(LINEST(known_y'er;known_x'er);1)

  Y-skæringspunkt:
  =INDEKS(LINEST(known_y'er;known_x'er);2)

• Linjens nøjagtighed, der er beregnet med funktionen LINREGR, afhænger af spredningsgraden for de anvendte data. Jo mere lineære dataene er, jo mere nøjagtig er LINREGR-modellen. LINREGR bruger de mindste kvadraters metode til at bestemme den bedste tilnærmelse til dataene, og returnerer derefter en matrix, der beskriver linjen. Når der kun er én uafhængig x-variabel, baseres beregningerne for m og b på følgende formler:

  

  

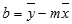
  hvor x og y er stikprøvernes middelværdi, dvs. x = MIDDEL(kendte_x'er) og y = MIDDEL(kendte_y'er)).

• Funktionerne STREGER OG LOGREGENST kan bruges til at beregne den bedste lige kurve eller eksponentialkurve, der passer til dine data. Du skal dog beslutte, hvilket af de to resultater der passer bedst til dine data. Du kan beregne TENDENS(known_y'er,known_x'er) for en lige linje eller VÆKST(known_y'erknown_x) for en eksponentialkurve. Disse funktioner returnerer uden argumentet new_x en matrix med y-værdier, der er forudsagt langs den pågældende linje eller kurve ved dine faktiske datapunkter. Du kan derefter sammenligne de forudsagte værdier med de faktiske værdier. Det kan være en god ide at lave diagrammer ud fra dem begge som en visuel sammenligning.

• Ved regressionsanalyse beregnes for hvert punkt den kvadrerede forskel mellem den skønnede y-værdi for det pågældende punkt og den faktiske y-værdi. Summen af disse kvadrerede forskelle kaldes kvadraternes restsum, ksrest. Derefter beregnes den totale sum af kvadrater, sstotal. Når argumentet konstant = SAND eller er udeladt, er den totale sum af kvadrater lig med summen af de kvadrerede forskelle mellem de faktiske y-værdier og gennemsnitsværdien for y-værdierne. Når argumentet konstant = FALSK, er den totale sum af kvadrater lig med summen af kvadrater af de faktiske y-værdier (uden at trække den gennemsnitlige y-værdi fra hver individuel y-værdi). Derefter kan regressionssummen af kvadrater, ksreg, findes ud fra: ksreg = sstotal - ksrest. Jo mindre restsummen af kvadrater er sammenlignet med den samlede sum af kvadrater, jo større er værdien af determinationskoefficienten r^2,som er et symbol for, hvor godt ligningen i regressionsanalysen beskriver forholdet mellem variablerne. Værdien af r^{2 er} lig med ssreg/sstotal.

• I nogle tilfælde har en eller flere af X-kolonnerne (antag, at Y’er og X’er er i kolonner) ingen ekstra skønnet værdi ved tilstedeværelse af de andre X-kolonner. Med andre ord kan udeladelse af en eller flere X-kolonner føre til skønnede Y-værdier, der er lige præcise. I dette tilfælde skal disse redundante X-kolonner udelades fra regressionsmodellen. Dette fænomen kaldes “kollinearitet”, fordi eventuelle redundante X-kolonner kan udtrykkes som en sum af multipler af de ikke-redundante X-kolonner. Funktionen LINREGR kontrollerer, om der er kollinearitet og fjerner eventuelle redundante X-kolonner fra regressionsmodellen, når de identificeres. Fjernede X-kolonner kan genkendes i LINREGR-output, derved at de har både 0-koefficienter og 0 se-værdier. Hvis en eller flere kolonner fjernes som redundante, berøres fg, fordi fg afhænger af antallet af X-kolonner, der faktisk bruges til skønsformål. Yderligere oplysninger om beregning af fg findes i Eksempel 4 nedenfor. Hvis fg ændres, fordi redundante X-kolonner fjernes, berøres værdierne af sey og F også. Kollinearitet bør i praksis være relativ sjælden. Der er dog ét tilfælde, hvor det mere sandsynligt kan forekomme, nemlig når nogle X-kolonner kun indeholder 0- og 1-værdier som indikatorer for, om et individ i et eksperiment er medlem af en bestemt gruppe eller ej. Hvis konstant = SAND eller udeladt, indsætter funktionen LINREGR effektivt en ekstra X-kolonne for alle 1’er for at beregne skæringspunktet. Hvis du har en kolonne med et 1 for hvert individ, hvis det er hankøn, og 0 hvis ikke, og du også har en kolonne med 1 for hvert individ, hvis det er hunkøn, og 0 hvis ikke, er den sidste kolonne redundant, fordi posterne i den kan udledes ved at trække posten i kolonnen med “hankønsindikator” fra posten i den ekstra kolonne med alle 1’er tilføjet af funktionen LINREGR.

• Værdien af f beregnes på følgende måde, når der ikke fjernes X-kolonner fra modellen på grund af kollidaritet: Hvis der er k-kolonner med known_x'er, og konstant = SAND eller udelades, er fg = n – k – 1. Hvis konstant = FALSK, er f = n - k. I begge tilfælde øger hver X-kolonne, der blev fjernet på grund af kollidaritet, værdien af fg med 1.

• Når du indtaster en matrixkonstant (f.eks. known_x'er)som argument, skal du bruge kommaer til at adskille værdier i samme række og semikolon til at adskille rækker. Separatortegn kan variere afhængigt af de internationale indstillinger.

• Bemærk, at y-værdierne, der er skønsmæssigt beregnet med regressionsligningen, eventuelt ikke er gyldige, hvis de ligger uden for intervallet for de y-værdier, du har anvendt til at udregne ligningen.

• Den underliggende algoritme, der bruges i funktionen LINEST, er forskellig fra den underliggende algoritme, der bruges i funktionerne STIGNINGog SKÆRING. Forskellen mellem disse algoritmer kan føre til forskellige resultater, når data er ubestemte og ligger på samme linje. Hvis f.eks. datapunkterne for argumentet known_y er 0, og datapunkterne for argumentet known_x er 1:

  • LINREGR returnerer en værdi på 0. Algoritmen for funktionen LINREGR er designet til at returnere rimelige resultater for data på samme linje, og i dette tilfælde kan der findes mindst ét svar.

  • STIGNING og SKÆRING returnerer et #DIV/0! som fejl. Algoritmen for funktionerne STIGNINGog SKÆRING er designet til kun at søge efter ét svar, og i dette tilfælde kan der være mere end ét svar.

• Ud over at bruge LOGREGR til at beregne statistik for andre regressionstyper kan du bruge LINREGR til at beregne en række andre regressionstyper ved at indtaste funktionerne for x- og y-variablerne som x- og y-serien for LINEST, f.eks. følgende formel:

  =LINREGR(yværdier; xværdier^KOLONNE($A:$C))

  fungerer, hvis du har en enkelt kolonne med y-værdier og en enkelt kolonne med x-værdier til at beregne den kubiske (polynomisk af tredje orden) tilnærmelse af formlen:

  y = m1*x + m2*x^2 + m3*x^3 + b

  Du kan justere denne formel for at beregne andre regressionstyper, men i nogle tilfælde kræver det, at outputværdierne og anden statistik justeres.

• Den værdi for F-testen, der returneres af funktionen LINREGR, adskiller sig fra den værdi for F-testen, der returneres af funktionen FTEST. LINREGR returnerer F-statistikken, mens FTEST returnerer sandsynligheden.

Eksempler