In diesem Artikel werden die Formelsyntax und die Verwendung der Funktion KOVARIANZ.P in Microsoft Excel beschrieben.
Gibt die Kovarianz der Grundgesamtheit zurück, den Durchschnitt der Produkte der Abweichungen für jedes Datenpunktpaar in zwei Datasets. Die Kovarianz gibt Auskunft darüber, welcher Zusammenhang zwischen zwei Datengruppen besteht. Beispielsweise können Sie ermitteln, ob ein größeres Einkommen Folge des jeweiligen Ausbindungsgrads ist.
Syntax
KOVARIANZ.P(Matrix1;Matrix2)
Die Syntax der Funktion KOVARIANZ.P weist die folgenden Argumente auf:
-
Matrix1 Erforderlich. Der erste Zellbereich, dessen Zellen mit ganzen Zahlen belegt sind.
-
Matrix2 Erforderlich. Der zweite Zellbereich, dessen Zellen mit ganzen Zahlen belegt sind.
Hinweise
-
Als Argumente müssen entweder Zahlen oder Namen, Matrizen bzw. Bezüge angegeben werden, die Zahlen enthalten.
-
Enthält ein als Matrix oder Bezug angegebenes Argument Text, Wahrheitswerte oder leere Zellen, werden diese Werte ignoriert. Zellen, die den Wert 0 enthalten, werden dagegen berücksichtigt.
-
Verfügen Matrix1 und Matrix2 nicht über dieselbe Anzahl von Datenpunkten, gibt KOVARIANZ.P den Fehlerwert #NV zurück.
-
Ist eine der beiden Matrizen Matrix1 oder Matrix2 leer, gibt KOVARIANZ.P den Fehlerwert #DIV/0! zurück.
-
Die Kovarianz wird wie folgt berechnet:
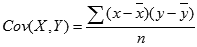
Dabei gilt:
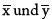
sind die Stichprobenmittelwerte MITTELWERT(Matrix1) und MITTELWERT(Matrix2), und n ist der Stichprobenumfang.
Beispiel
Kopieren Sie die Beispieldaten in der folgenden Tabelle, und fügen Sie sie in Zelle A1 eines neuen Excel-Arbeitsblatts ein. Um die Ergebnisse der Formeln anzuzeigen, markieren Sie sie, drücken Sie F2 und dann die EINGABETASTE. Im Bedarfsfall können Sie die Breite der Spalten anpassen, damit alle Daten angezeigt werden.
|
Daten1 |
Daten2 |
|
|
3 |
9 |
|
|
2 |
7 |
|
|
4 |
12 |
|
|
5 |
15 |
|
|
6 |
17 |
|
|
Formel |
Beschreibung |
Ergebnis |
|
=KOVARIANZ.P(A2:A6;B2:B6) |
Die Kovarianz, d. h. der Mittelwert der für alle angegebenen Datenpunktpaare gebildeten Produkte der Abweichungen. |
5,2 |










