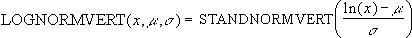In diesem Artikel werden die Formelsyntax und die Verwendung der Funktion LOGNORMVERT in Microsoft Excel beschrieben.
Beschreibung
Gibt Werte der Verteilungsfunktion einer lognormalverteilten Zufallsvariablen zurück, wobei ln(x) mit den Parametern Mittelwert und Standabwn normalverteilt ist. Mit dieser Funktion können Sie Daten untersuchen, die logarithmisch transformiert wurden.
Wichtig: Diese Funktion wurde durch eine oder mehrere neue Funktionen ersetzt, die ggf. eine höhere Genauigkeit bieten und deren Namen die Verwendung besser wiedergeben. Obwohl diese Funktion aus Gründen der Abwärtskompatibilität weiterhin verfügbar ist, sollten Sie von nun an die neuen Funktionen verwenden, da die alte Funktion in zukünftigen Versionen von Excel möglicherweise nicht mehr verfügbar sein wird.
Weitere Informationen zur neuen Funktion finden Sie unter LOGNORM.VERT (Funktion).
Syntax
LOGNORMVERT(x;Mittelwert;Standabwn)
Die Syntax der Funktion LOGNORMVERT weist die folgenden Argumente auf:
-
x Erforderlich. Der Wert, für den die Funktion ausgewertet werden soll
-
Mittelwert Erforderlich. Der Mittelwert der Lognormalverteilung
-
Standabwn Erforderlich. Die Standardabweichung der Lognormalverteilung
Hinweise
-
Wenn ein Argument nicht numerisch ist, gibt LOGNORMDIST die #VALUE! zurückgegeben.
-
Wenn x ≤ 0 oder 0 Standard_dev ≤, gibt LOGNORMDIST die #NUM! zurückgegeben.
-
Die Gleichung für die Verteilungsfunktion einer logarithmischen Normalverteilung lautet:
Beispiel
Kopieren Sie die Beispieldaten in der folgenden Tabelle, und fügen Sie sie in Zelle A1 eines neuen Excel-Arbeitsblatts ein. Um die Ergebnisse der Formeln anzuzeigen, markieren Sie sie, drücken Sie F2 und dann die EINGABETASTE. Im Bedarfsfall können Sie die Breite der Spalten anpassen, damit alle Daten angezeigt werden.
|
Daten |
Beschreibung |
|
|
4 |
Wert, für den die Funktion ausgewertet werden soll (x) |
|
|
3,5 |
Mittelwert von ln(x) |
|
|
1,2 |
Standardabweichung von ln(x) |
|
|
Formel |
Beschreibung |
Ergebnis |
|
=LOGNORMVERT(A2;A3;A4) |
Wert der Verteilungsfunktion der Lognormalverteilung für 4 mit den oben angegebenen Bedingungen |
0,0390836 |