Returns the normal distribution for the specified mean and standard deviation. This function has a very wide range of applications in statistics, including hypothesis testing.
Important: This function has been replaced with one or more new functions that may provide improved accuracy and whose names better reflect their usage. Although this function is still available for backward compatibility, you should consider using the new functions from now on, because this function may not be available in future versions of Excel.
For more information about the new function, see NORM.DIST function.
Syntax
NORMDIST(x,mean,standard_dev,cumulative)
The NORMDIST function syntax has the following arguments:
-
X Required. The value for which you want the distribution.
-
Mean Required. The arithmetic mean of the distribution.
-
Standard_dev Required. The standard deviation of the distribution.
-
Cumulative Required. A logical value that determines the form of the function. If cumulative is TRUE, NORMDIST returns the cumulative distribution function; if FALSE, it returns the probability mass function.
Remarks
-
If mean or standard_dev is nonnumeric, NORMDIST returns the #VALUE! error value.
-
If standard_dev ≤ 0, NORMDIST returns the #NUM! error value.
-
If mean = 0, standard_dev = 1, and cumulative = TRUE, NORMDIST returns the standard normal distribution, NORMSDIST.
-
The equation for the normal density function (cumulative = FALSE) is:
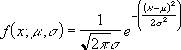
-
When cumulative = TRUE, the formula is the integral from negative infinity to x of the given formula.
Example
Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.
|
Data |
Description |
|
|
42 |
Value for which you want the distribution |
|
|
40 |
Arithmetic mean of the distribution |
|
|
1.5 |
Standard deviation of the distribution |
|
|
Formula |
Description |
Result |
|
=NORMDIST(A2,A3,A4,TRUE) |
Cumulative distribution function for the terms above |
0.9087888 |
|
=NORMDIST(A2,A3,A4,FALSE) |
Probability mass function for the terms above |
0.10934 |