Returns the confidence interval for a population mean with a normal distribution. The confidence interval is a range on either side of a sample mean. For example, if you order a product through the mail, you can determine, with a particular level of confidence, the earliest and latest the product will arrive.
Syntax
CONFIDENCE(alpha,standard_dev,size)
Alpha is the significance level used to compute the confidence level. The confidence level equals 100*(1 - alpha)%, or in other words, an alpha of 0.05 indicates a 95 percent confidence level.
Standard_dev is the population standard deviation for the data range and is assumed to be known.
Size is the sample size.
Remarks
-
If any argument is nonnumeric, CONFIDENCE returns the #VALUE! error value.
-
If alpha ≤ 0 or alpha ≥ 1, CONFIDENCE returns the #NUM! error value.
-
If standard_dev ≤ 0, CONFIDENCE returns the #NUM! error value.
-
If size is not an integer, it is truncated.
-
If size < 1, CONFIDENCE returns the #NUM! error value.
-
If we assume alpha equals 0.05, we need to calculate the area under the standard normal curve that equals (1 - alpha), or 95 percent. This value is ± 1.96. The confidence interval is therefore:
Example
Suppose we observe that, in our sample of 50 commuters, the average length of travel to work is 30 minutes with a population standard deviation of 2.5. We can be 95 percent confident that the population mean is in the interval:
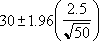
|
Alpha |
StdDev |
Size |
Formula |
Description (Result) |
|---|---|---|---|---|
|
0.05 |
.5 |
50 |
=CONFIDENCE([Alpha],[StdDev],[Size]) |
Confidence interval for a population mean. In other words, the average length of travel to work equals 30 ± 0.692951 minutes, or 29.3 to 30.7 minutes. (0.692951) |