This topic covers the different trendline options that are available in Office.
Use this type of trendline to create a best-fit straight line for simple linear data sets. Your data is linear if the pattern in its data points looks like a line. A linear trendline usually shows that something is increasing or decreasing at a steady rate.
A linear trendline uses this equation to calculate the least squares fit for a line:
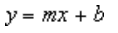
where m is the slope and b is the intercept.
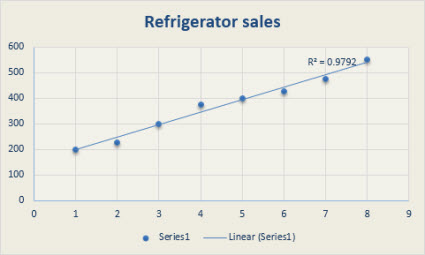
The following linear trendline shows that refrigerator sales have consistently increased over an 8-year period. Notice that the R-squared value (a number from 0 to 1 that reveals how closely the estimated values for the trendline correspond to your actual data) is 0.9792, which is a good fit of the line to the data.
Showing a best-fit curved line, this trendline is useful when the rate of change in the data increases or decreases quickly and then levels out. A logarithmic trendline can use negative and positive values.
A logarithmic trendline uses this equation to calculate the least squares fit through points:
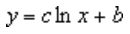
where c and b are constants and ln is the natural logarithm function.
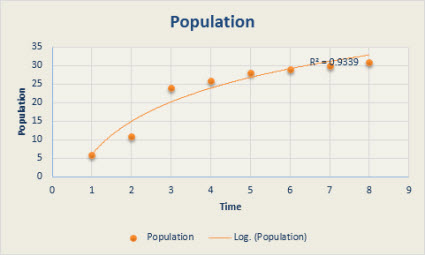
The following logarithmic trendline shows predicted population growth of animals in a fixed-space area, where population leveled out as space for the animals decreased. Note that the R-squared value is 0.933, which is a relatively good fit of the line to the data.
This trendline is useful when your data fluctuates. For example, when you analyze gains and losses over a large data set. The order of the polynomial can be determined by the number of fluctuations in the data or by how many bends (hills and valleys) appear in the curve. Typically, an Order 2 polynomial trendline has only one hill or valley, an Order 3 has one or two hills or valleys, and an Order 4 has up to three hills or valleys.
A polynomial or curvilinear trendline uses this equation to calculate the least squares fit through points:
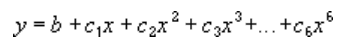
where b and 
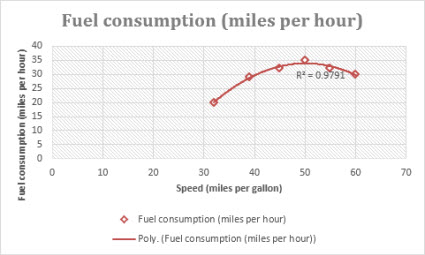
The following Order 2 polynomial trendline (one hill) shows the relationship between driving speed and fuel consumption. Notice that the R-squared value is 0.979, which is close to 1 so the line’s a good fit to the data.
Showing a curved line, this trendline is useful for data sets that compare measurements that increase at a specific rate. For example, the acceleration of a race car at 1-second intervals. You cannot create a power trendline if your data contains zero or negative values.
A power trendline uses this equation to calculate the least squares fit through points:
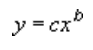
where c and b are constants.
Note: This option is not available when your data includes negative or zero values.
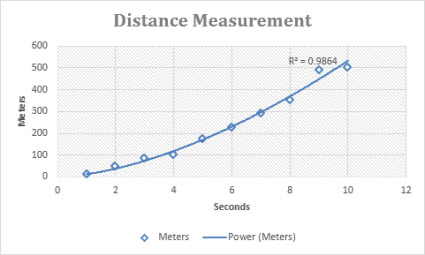
The following distance measurement chart shows distance in meters by seconds. The power trendline clearly demonstrates the increasing acceleration. Note that the R-squared value is 0.986, which is an almost perfect fit of the line to the data.
Showing a curved line, this trendline is useful when data values rise or fall at constantly increasing rates. You cannot create an exponential trendline if your data contains zero or negative values.
An exponential trendline uses this equation to calculate the least squares fit through points:
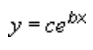
where c and b are constants and e is the base of the natural logarithm.
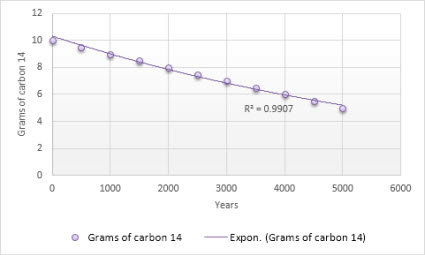
The following exponential trendline is shows the decreasing amount of carbon 14 in an object as it ages. Note that the R-squared value is 0.990, which means the line fits the data almost perfectly.
This trendline evens out fluctuations in data to show a pattern or trend more clearly. A moving average uses a specific number of data points (set by the Period option), averages them, and uses the average value as a point in the line. For example, if Period is set to 2, the average of the first two data points is used as the first point in the moving average trendline. The average of the second and third data points is used as the second point in the trendline, etc.
A moving average trendline uses this equation:
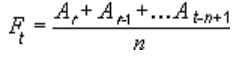
The number of points in a moving average trendline equals the total number of points in the series, minus the number you specify for the period.
In a scatter chart, the trendline is based on the order of the x values in the chart. For a better result, sort the x values before you add a moving average.
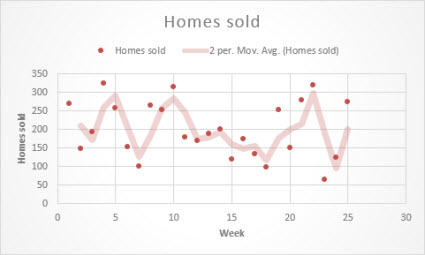
The following moving average trendline shows a pattern in the number of homes sold over a 26-week period.
Important: Beginning with Excel version 2005, Excel adjusted the way it calculates the R2 value for linear trendlines on charts where the trendline intercept is set to zero (0). This adjustment corrects calculations that yielded incorrect R2 values and aligns the R2 calculation with the LINEST function. As a result, you may see different R2 values displayed on charts previously created in prior Excel versions. For more information, see Changes to internal calculations of linear trendlines in a chart.
Need more help?
You can always ask an expert in the Excel Tech Community or get support in Communities.