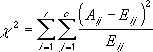Devuelve la prueba de independencia. PRUEBA.CHI devuelve el valor de la distribución chi cuadrado (χ2) para la estadística y los grados de libertad apropiados. Las pruebas χ2 pueden usarse para determinar si un experimento se ajusta a los resultados teóricos.
Importante: Esta función se ha sustituido por una o más funciones nuevas que pueden proporcionar una precisión mejorada y cuyos nombres reflejan mejor su uso. Aunque esta función sigue estando disponible para la compatibilidad con versiones anteriores, a partir de ahora debe considerar el uso de las funciones nuevas, ya que puede que esta función no esté disponible en futuras versiones de Excel.
Para más información sobre la nueva función, consulte Función PRUEBA.CHICUAD.
Sintaxis
PRUEBA.CHI(rango_real;rango_esperado)
La sintaxis de la función PRUEBA.CHI tiene los siguientes argumentos:
-
Rango_real Obligatorio. El rango de datos que contiene las observaciones que se contrastarán con los valores esperados.
-
Rango_esperado Obligatorio. El rango de datos que contiene la relación del producto de los totales de filas y columnas con el total global.
Observaciones
-
Si rango_real y rango_esperado tienen un número diferente de puntos de datos, PRUEBA.CHI devuelve el valor de error #N/A.
-
La prueba χ2 primero calcula una estadística χ2 usando la fórmula:
donde:
Aij = frecuencia real en la i-ésima fila, j-ésima columna
Eij = frecuencia esperada en la i-ésima fila, j-ésima columna
r = número de filas
c = número de columnas
-
Un valor bajo de χ2 es un indicador de independencia. Como se puede ver en la fórmula, χ2 siempre es positivo o 0, y es 0 solo si Aij = Eij para todo i,j.
-
PRUEBA.CHI devuelve la probabilidad de que un valor de la estadística χ2 como mínimo tan elevado como el valor calculado mediante la fórmula anterior pueda haberse producido al azar en el supuesto de independencia. Al calcular esta probabilidad, PRUEBA.CHI usa la distribución χ2 con un número adecuado de grados de libertad, df. Si r > 1 y c > 1, entonces df = (r - 1)(c - 1). Si r = 1 y c > 1, entonces df = c - 1 o si r > 1 y c = 1, entonces df = r - 1. r = c= 1 no está permitido y se devuelve #N/A.
-
Es más apropiado usar PRUEBA.CHI cuando Eij no son demasiado pequeños. Algunos estadísticos sugieren que cada Eij debería ser mayor o igual a 5.
Ejemplo
Copie los datos de ejemplo en la tabla siguiente y péguelos en la celda A1 de una hoja de cálculo nueva de Excel. Para que las fórmulas muestren los resultados, selecciónelas, presione F2 y luego ENTRAR. Si lo necesita, puede ajustar el ancho de las columnas para ver todos los datos.
|
Hombres (Real) |
Mujeres (Real) |
Descripción |
|
58 |
35 |
Están de acuerdo |
|
11 |
25 |
Neutra |
|
10 |
23 |
No están de acuerdo |
|
Hombres (Esperado) |
Mujeres (Esperado) |
Descripción |
|
45,35 |
47,65 |
Están de acuerdo |
|
17,56 |
18,44 |
Neutra |
|
16,09 |
16,91 |
No están de acuerdo |
|
Fórmula |
Descripción |
Resultado |
|
=PRUEBA.CHI(A2:B4;A6:B8) |
La estadística χ2 de los datos anteriores es 16,16957 con 2 grados de libertad. |
0,0003082 |