Selles artiklis kirjeldatakse Microsoft Exceli funktsiooni LINEST valemisüntaksit ja kasutamist.
Kirjeldus
Funktsioon LINEST arvutab vähimruutude meetodil statistikud joonele, mis parimal viisil sobitub andmetega ja tagastab seda joont kirjeldava massiivi. Muud tüüpi mudelite korral, mis on tundmatutes parameetrites (s.h polünoomi-, logaritmi-, eksponent- ja astendusseeriad) lineaarsed, võib statistikute arvutamisel funktsiooni LINEST kombineerida ka teiste funktsioonidega. Kuna see funktsioon tagastab väärtuste massiivi, tuleb ta sisestada massiivivalemina. Juhised leiate käesoleva artikli näidetest.
Sirge võrrand on:
y = mx + b
– või –
y = m1x1 + m2x2 + ... + b
kui on mitu x-väärtuste vahemikku, kus sõltuvad y-väärtused on sõltumatute x-väärtuste funktsioon. m-väärtused on igale x-väärtusele vastavad kordajad ja b on konstant. Võtke arvesse, et y, x ja m võivad olla vektorid. Funktsioon LINEST tagastab massiivi {mn\mn-1\...\m1\b}. LINEST võib tagastada ka täiendavaid regressioonistatistikuid.
Süntaks
LINEST(teada_y_väärtused;[teada_x_väärtused];[konstant];[statistika])
Funktsiooni LINEST süntaksil on järgmised argumendid.
Süntaks
-
teada_y_väärtused – nõutav. Y-väärtuste kogum, mis on juba teada seoses y = mx + b.
-
Kui vahemik teada_y_väärtused on ühes veerus, tõlgendatakse vahemiku teada_x_väärtused iga veergu eraldi muutujana.
-
Kui vahemik teada_y_väärtused on ühes reas, tõlgendatakse vahemiku teada_x_väärtused iga rida eraldi muutujana.
-
-
teada_x_väärtused – valikuline. X-väärtuste kogum, mis võib juba olla teada seoses y = mx + b.
-
Vahemik teada_x_väärtused võib sisaldada ühte või enamat muutujate hulka. Kui kasutate ainult ühte muutujat, võivad teada_y_väärtused ja teada_x_väärtused olla suvalise kujuga vahemikud, kuid neil peavad olema võrdsed mõõtmed. Kui kasutate enam kui ühte muutujat, peab argument teada_y_väärtused olema vektor (st ühe rea kõrgusega või ühe veeru laiusega vahemik.)
-
Kui argument teada_x_väärtused puudub, eeldatakse, et see on massiiv {1\2\3\...}, millel on sama suurus kui massiivil teada_y_väärtused.
-
-
konstant – valikuline. Loogikaväärtus, mis määrab, kas konstant b peab võrduma nulliga.
-
Kui konstant on väärtusega TRUE või ära jäetud, arvutatakse b tavalisel viisil.
-
Kui konstant on FALSE, seatakse b võrdseks nulliga ja reguleeritakse m-väärtusi nii, et kehtiks võrdus y = mx.
-
-
statistikud – valikuline. Loogikaväärtus, mis määrab, kas tagastada täiendavad regressioonistatistikud.
-
Kui statistika on TRUE, tagastab funktsioon LINEST täiendavad regressioonistatistikud; seetõttu on tagastatud massiiv {mn\mn-1,...,m1\b; sen,sen-1,...,se1,seb; r2,sey; F,df; ssreg,ssresid}.
-
Kui argument statistikud on FALSE või puudub, tagastab funktsioon LINEST ainult m-kordajad ja konstandi b.
Täiendavad regressioonistatistikud on järgmised.
-
|
Statistikud |
Kirjeldus |
|---|---|
|
se1,se2,...,sen |
Kordajate m1, m2, ..., mn standardvigade väärtused |
|
seb |
Konstandi b standardhälbe väärtus (seb = #N/A, kui konstant on FALSE) |
|
r2 |
Determinatsioonikordaja. Võrdleb hinnangulisi ja tegelikke y-väärtusi ning on väärtusega nullist üheni. Kui see on 1, siis on valimi korrelatsioon täpne – hinnangulise y-väärtuse ja tegeliku y-väärtuse vahel pole erinevust. Teises äärmuses, kui determinatsioonikordaja on null, pole regressioonivõrrandist y-väärtuse prognoosimisel abi. Lisateavet2 arvutamise kohta leiate selle teema jaotisest "Kommentaarid". |
|
sey |
Muutuja y hinnangu standardviga |
|
F |
F-statistik ehk F-statistiku vaadeldav väärtus. Kasutage F-statistikut, et teha kindlaks, kas sõltuvate ja sõltumatute muutujate vaadeldud seos on juhuslik. |
|
df |
Vabadusastmed. Kasutage vabadusastmeid, et leida statistilises tabelis F-statistiku kriitilisi väärtusi. Võrrelge tabelist leitud väärtusi funktsiooni LINEST tagastatud F-statistikuga, et määrata mudeli usaldusaste. Teavet sellest, kuidas arvutatakse suurust df, leiate allpool lõigus "Kommentaarid". Näide 4 näitab suuruste F ja df kasutamist. |
|
ssreg |
Regressiooniruutude summa. |
|
ssresid |
Jäägiruutude summa. Teavet sellest, kuidas arvutatakse suurusi ssreg ja ssresid, leiate allpool lõigus "Kommentaarid". |
Järgmine näide illustreerib täiendavate regressioonistatistikute tagastamise järjekorda.

Kommentaarid
-
Iga sirgjoont saab kirjeldada tõusu ja algordinaadiga:
Tõus (m):
Joone kalle leidmiseks, mis on sageli kirjutatud kui m, võtke joonel kaks punkti: (x1,y1) ja (x2,y2); tõus võrdub (y2 - y1)/(x2 - x1).Algordinatsioon (b):
Joone algordinatsioon, mis on sageli kirjutatud kui b, on väärtus y kohas, kus joon lõikub y-teljega.Sirgjoone võrrand on y = mx + b. Kui teate suuruste m ja b väärtusi, võite arvutada välja suvalise punkti joonel, asetades sellesse võrrandisse y- või x-väärtuse. Samuti võite kasutada funktsiooni TREND.
-
Kui on ainult üks sõltumatu x-muutuja, võite saada tõusu ja algordinaadi väärtused otse järgmistest valemitest:
Nõlv:
=INDEX(LINEST(known_y;known_x oma);1)Algordinatsioon:
=INDEX(LINEST(known_y;known_x oma);2) -
Funktsiooni LINEST arvutatud sirgjoone täpsus sõltub andmete hajuvuse astmest. Mida lineaarsemad on andmed, seda täpsem on funktsiooni LINEST mudel. Funktsioon LINEST kasutab vähimruutude meetodit andmete parimaks sobituseks. Kui on ainult üks sõltumatu x-muutuja, põhinevad suuruste m ja b arvutused järgmistel valemitel.
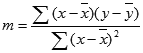
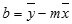
kus x ja y on valimi keskmised, st x = AVERAGE(teada_x_väärtused) ja y = (teada_y_väärtused).
-
Joone- ja kõverafunktsioonid LINEST ja LOGEST saavad arvutada parima sirgjoone või eksponentkõvera, mis sobib teie andmetega. Siiski peate otsustama, milline kahest tulemusest sobib teie andmetega kõige paremini. Eksponentkõvera korral saate funktsiooni TREND(known_y;known_xomad) arvutamiseks kasutada sirgjoont või funktsiooni GROWTH(known_y,known_x oma). Need funktsioonid tagastavad ilma new_x argumendita y-väärtuste massiivi, mis on ennustatud piki seda joont või kõverat teie tegelikes andmepunktides. Seejärel saate võrrelda prognoositud väärtusi tegelike väärtustega. Võimalik, et soovite neid mõlemaid visuaalse võrdluse jaoks diagrammina esitada.
-
Exceli regressioonanalüüs arvutab igale andmepunktile hinnangulise y-väärtuse ja tegeliku y-väärtuse vahe ruudu. Nende vahede ruutude summat nimetatakse jäägiruutude summaks (ssresid). Excel arvutab seejärel ruutude kogusumma (sstotal). Kui argument konstant = TRUE või puudub, võrdub ruutude kogusumma tegelike y-väärtuste ja nende keskmise vahede ruutude summaga. Kui argument konstant = FALSE, võrdub ruutude kogusumma tegelike y-väärtuste ruutude summaga (y-väärtuste keskmist ei lahutata igast üksikust y-väärtusest). Sel juhul võib jäägiruutude summa ssreg leida valemiga: ssreg = sstotal - ssresid. Mida väiksem on jääkruutude summa, seda suurem on ruutude kogusummaga võrreldes see, mida suurem on määramiskordaja r2 väärtus, mis näitab, kui hästi regressioonianalüüsi tulemus võrrand seletab seost muutujate vahel. R2 väärtus võrdub ssreg/sstotal.
-
Mõnel juhul võib ühel või mitmel x-väärtuste veerul (eeldades, et y-väärtused ja x-väärtused on antud veergudena) puududa täiendav ennustav väärtus teiste X-veergude olemasolu korral. Teisisõnu võib ühe või mitme X-veeru kõrvaldamine anda tulemuseks niisama täpselt ennustatud y-väärtused. Sellisel juhul tuleb need liiased X-veerud regressioonimudelist välja jätta. Seda nähtust nimetatakse "kolineaarsuseks", kuna suvalist liiast X-veergu saab esitada mitme mitteliiase X-veeru summana. Funktsioon LINEST kontrollib kolineaarsust ja eemaldab regressioonimudelist kõik liiased X-veerud, kui need on tuvastatud. Eemaldatud X-veerge saab funktsiooni LINEST väljundis ära tunda 0-väärtustega kordajate ning 0-väärtustega standardvigade se järgi. Kui üks või mitu liiast veergu eemaldatakse, mõjutab see vabadusastmeid df, kuna df sõltub ennustuseks tegelikult kasutatud X-veergude arvust. Üksikasju vabadusastmete df arvutamise kohta vt näitest 4. Kui df muutub liiaste X-veergude eemaldamise tõttu, mõjutab see ka standardvea sey ja statistiku F väärtusi. Kolineaarsus on praktikas üsna haruldane. Üks juhtum, kus see võib tõenäoliselt esineda, on see, kus mõned X-veerud sisaldavad ainult arve 0 ja 1, mis näitavad, kas eksperimendis osalev subjekt on teatud rühma liige või mitte. Kui konstant = TRUE või puudub, lisab LINEST tegelikult täiendava ainult 1-dest koosneva X-veeru algordinaadi mudelisse. Kui teil on üks veerg, milles 1 tähistab meessoost isikuid ja 0 naissoost isikuid, ning teine veerg, milles 1 tähistab naissoost isikuid ja 0 meessoost isikuid, siis on teine veerg liiane, kuna selle kirjed saab arvutada, lahutades "meeste veeru" kirje täiendava ainult 1-dest koosneva X-veeru kirjest, mille lisab funktsioon LINEST.
-
Kui mudelist ei eemaldata ühtki X-veergu kolineaarsuse tõttu, arvutatakse vabadusastmeid df järgmiselt: kui k-veerud on teada_x_väärtused ja konstant = TRUE või puudub, siis df = n – k – 1. Kui konstant = FALSE, siis df = n - k. Mõlemal juhul suurendab iga X-veeru kõrvaldamine kolineaarsuse tõttu suurust df ühe võrra.
-
Sisestades argumendina massiivikonstandi (nt teada_x_väärtused), kasutage kurakaldkriipse (\) sama rea väärtuste eraldamiseks ja semikooloneid erinevate ridade eraldamiseks. Eraldajad võivad sõltuvalt teie piirkonnasätetest erineda.
-
Pange tähele, et regressioonivalemi ennustatud y-väärtused ei pruugi olla lubatud, kui nad väljuvad y-väärtuste vahemikust, mida kasutasite valemi määramiseks.
-
Funktsioonis LINEST kasutatav põhialgoritm erineb funktsioonides SLOPE ja INTERCEPT kasutatavast põhialgoritmist. Määratlemata andmete ja joondusandmete korral võib nende algoritmide erinevus põhjustada erinevaid tulemusi. Oletagem näiteks, et argumendi teada_y_väärtused andmepunktid on 0 ja argumendi teada_x_väärtused andmepunktid on 1.
-
Funktsioon LINEST tagastab väärtuse 0. Funktsiooni LINEST algoritm on loodud tagastama joondusandmete mõistlikke tulemeid ja antud juhul leitakse vähemalt üks vastus.
-
SLOPE ja INTERCEPT tagastavad #DIV/0! #VALUE!. Funktsioonide SLOPE ja INTERCEPT algoritm on loodud otsima ainult ühte vastust ja antud juhul võib olla mitu vastust.
-
-
Lisaks funktsioonile LOGEST, mis arvutab teiste regressioonitüüpide statistikuid, võite teiste regressioonitüüpide vahemike arvutamiseks kasutada funktsiooni LINEST, sisestades x- ja y-muutujate funktsioonid LINEST-funktsiooni x- ja y-sarjadena. Näiteks järgmine valem:
=LINEST(y_väärtused; x-väärtused^COLUMN($A:$C))
toimib siis, kui järgmise valemikuju kuupaproksimatsiooni (järgu 3 polünoom) arvutamiseks on antud üks veerg y-väärtusi ja üks veerg x-väärtusi:
y = m1*x + m2*x^2 + m3*x^3 + b
Seda valemit võib kohandada teist tüüpi regressioonide arvutamiseks, kuid mõnel juhul eeldab see väljundväärtuste ja teiste statistikute reguleerimist.
-
Funktsiooni LINEST tagastatav F-testi väärtus erineb funktsiooni FTEST tagastatavast F-testi väärtusest. LINEST tagastab F-statistiku, FTEST seevastu tõenäosuse.
Näited
Näide 1: tõus ja algordinaat
Kopeerige järgmise tabeli näidisandmed ja kleepige need uue Exceli töövihiku lahtrisse A1. Selleks et valemid näitaksid tulemeid, valige need, vajutage klahvi F2 ja seejärel vajutage sisestusklahvi (Enter). Vajadusel saate kogu teabe nägemiseks veerulaiust muuta.
|
Teada y-väärtus |
Teada x-väärtus |
|---|---|
|
1 |
0 |
|
9 |
4 |
|
5 |
2 |
|
7 |
3 |
|
Tulem (tõus) |
Tulem (algordinaat) |
|
2 |
1 |
|
Valem (massiivivalem lahtrites A7:B7) |
|
|
=LINEST(A2:A5;B2:B5;;FALSE) |
Näide 2: lihtne lineaarregressioon
Kopeerige järgmise tabeli näidisandmed ja kleepige need uue Exceli töövihiku lahtrisse A1. Selleks et valemid näitaksid tulemeid, valige need, vajutage klahvi F2 ja seejärel vajutage sisestusklahvi (Enter). Vajadusel saate kogu teabe nägemiseks veerulaiust muuta.
|
Kuu |
Müük |
|---|---|
|
1 |
3100 € |
|
2 |
4500 € |
|
3 |
4400 € |
|
4 |
5400 € |
|
5 |
7500 € |
|
6 |
8100 € |
|
Valem |
Tulem |
|
=SUM(LINEST(B1:B6; A1:A6)*{9;1}) |
11 000 € |
|
Arvutab üheksanda kuu prognoositava müügi, võttes aluseks 1.–6. kuu müüginäitajad. |
Näide 3: mitmene lineaarregressioon
Kopeerige järgmise tabeli näidisandmed ja kleepige need uue Exceli töövihiku lahtrisse A1. Selleks et valemid näitaksid tulemeid, valige need, vajutage klahvi F2 ja seejärel vajutage sisestusklahvi (Enter). Vajadusel saate kogu teabe vaatamiseks veerulaiust muuta.
|
Põrandapind (x1) |
Bürood (x2) |
Sissepääsud (x3) |
Vanus (x4) |
Hinnanguline väärtus (y) |
|---|---|---|---|---|
|
2310 |
2 |
2 |
20 |
142 000 € |
|
2333 |
2 |
2 |
12 |
144 000 € |
|
2356 |
3 |
1,5 |
33 |
151 000 € |
|
2379 |
3 |
2 |
43 |
150 000 € |
|
2402 |
2 |
3 |
53 |
139 000 € |
|
2425 |
4 |
2 |
23 |
169 000 € |
|
2448 |
2 |
1,5 |
99 |
126 000 € |
|
2471 |
2 |
2 |
34 |
142 900 € |
|
2494 |
3 |
3 |
23 |
163 000 € |
|
2517 |
4 |
4 |
55 |
169 000 € |
|
2540 |
2 |
3 |
22 |
149 000 € |
|
-234,2371645 |
||||
|
13,26801148 |
||||
|
0,996747993 |
||||
|
459,7536742 |
||||
|
1732393319 |
||||
|
Valem (lahtrisse A19 sisestatud dünaamiline massiivivalem) |
||||
|
=LINEST(E2:E12;A2:D12;TRUE;TRUE) |
Näide 4: F- ja r2-statistika kasutamine
Eelmises näites on determinatsioonikordaja r2 0,99675 (vt funktsiooni LINEST väljundis lahtrit A17), mis osutaks tugevale seosele sõltumatute muutujate ja müügihinna vahel. Võite kasutada F-statistikut, et teha kindlaks, kas need nii kõrge r2 väärtusega tulemused on juhuslikud või mitte.
Oletagem hetkeks, et tegelikult muutujate vahel seos puudub, kuid 11 büroohoone juhuslik valim on selline, et statistiline analüüs näitab tugevat seost. Ekslike järelduste tõenäosust seoste olemasolu suhtes tähistatakse alfaga.
Funktsiooni LINEST väljundi F- ja df-väärtusi saab kasutada selleks, et hinnata tõenäosust, et F-väärtus on juhuslik. F-d saab võrrelda avaldatud F-jaotustabelites leiduvate kriitiliste väärtustega või exceli funktsiooni FDIST saab kasutada suurema F-väärtuse tõenäosuse arvutamiseks. Sobival F-jaotuses on v1 ja v2 vabadusastmed. Kui n on andmepunktide ja võistluste arv = TRUE või puudub, siis v1 = n – df – 1 ja v2 = df. (Kui const = FALSE, siis v1 = n – df ja v2 = df.) Funktsioon FDIST tagastab süntaksiga FDIST(F;v1;v2) suurema F-väärtuse tõenäosuse juhuslikult. Selles näites df = 6 (lahter B18) ja F = 459,753674 (lahter A18).
Eeldusel, et alfa väärtus on 0,05; v1 = 11 – 6 – 1 = 4 ja v2 = 6, on F-i kriitiline tase 4,53. Kuna F = 459,753674 on palju suurem kui 4,53, on äärmiselt ebatõenäoline, et F-väärtus, mis on nii kõrge, esines juhuslikult. (Kui alfa = 0,05, lükatakse tagasi hüpotees, et known_y ja known_x vahel puudub seos, kui F ületab kriitilise taseme 4,53.) Exceli funktsiooni FDIST abil saate saada tõenäosuse, et F-väärtus on nii suur kui juhuslik. Näiteks FDIST(459,753674; 4; 6) = 1,37E-7, äärmiselt väike tõenäosus. Võite järeldada, kas leides tabelist F kriitilise taseme või kasutades funktsiooni FDIST , et regressioonivõrrandist on kasu selles piirkonnas büroohoonete hinnangulise väärtuse ennustamisel. Pidage meeles, et eelmises lõigus arvutatud v1 ja v2 õigete väärtuste kasutamine on väga oluline.
Näide 5: t-statistiku arvutamine
Teise hüpoteesi kontrollimine teeb kindlaks, kas iga tõusukordaja on kasulik büroohoone väärtuse ennustamisel näites 3. Näiteks et kontrollida vanusekordajat statistilise olulisuse suhtes, jagage -234,24 (vanuse tõusukordaja) 13,268-ga (lahtri A15 vanusekordajate hinnanguline standardhälve). Järgnev on t-statistiku vaadeldav väärtus:
t = m4 ÷ se4 = -234.24 ÷ 13.268 = -17.7
Kui t absoluutväärtus on piisavalt kõrge, võib järeldada, et tõus on kasulik büroohoonete hinnangulise väärtuse arvutamisel näites 3. Järgmine tabel näitab nelja t-statistiku vaadeldavaid absoluutväärtusi.
Kui uurite tabelit statistikakäsiraamatus, leiate, et kahepoolne kuue vabadusastmega ja parameetriga alfa = 0,05 t-statistiku kriitiline väärtus on 2,447. Kriitilise väärtuse saab leida ka Exceli funktsiooni TINV abil. TINV(0,05;6) = 2,447. Kuna t absoluutväärtus (17,7) on suurem kui 2,447, on büroohoone vanus selle väärtuse ennustamisel oluliseks muutujaks. Iga teist sõltumatut muutujat saab statistilise olulisuse suhtes kontrollida samal viisil. Järgnevalt on antud iga sõltumatu muutuja t-statistiku vaadeldavad väärtused.
|
Muutuja |
t-statistiku vaadeldav väärtus |
|---|---|
|
põrandapind |
5,1 |
|
büroode arv |
31,3 |
|
sissepääsude arv |
4,8 |
|
vanus |
17,7 |
Kõigi nende väärtuste absoluutväärtused on suuremad kui 2,447; seetõttu on kõik regressioonivalemis kasutatud muutujad olulised antud ala büroohoonete väärtuse ennustamisel.










