Seda artiklit on kohandanud Microsoft Exceli andmeanalüüs ja äri modelleerimine Wayne L. Winston poolt.
-
Kes kasutab Monte Carlo simulatsiooni?
-
Mis juhtub, kui tipite lahtrisse =RAND() ?
-
Kuidas simuleerida diskreetse juhusliku muutuja väärtusi?
-
Kuidas simuleerida tavalise juhusliku muutuja väärtusi?
-
Kuidas saab tervituskaardi ettevõte määrata, mitu kaarti toota?
Soovime täpselt hinnata ebakindlate sündmuste tõenäosust. Näiteks milline on tõenäosus, et uue toote rahavoogudel on positiivne praegune puhasväärtus (NPV)? Milline on meie investeerimisportfelli riskitegur? Monte Carlo simulatsioon võimaldab meil modelleerida olukordi, mis tekitavad ebakindlust ja mängivad neid siis arvutis tuhandeid kordi.
Märkus.: Nimi Monte Carlo simulatsioon pärineb arvuti simulatsioonidest, mis viidi läbi 1930ndatel ja 1940ndatel, et hinnata tõenäosust, et aatomipommi detoneerimiseks vajalik ahelreaktsioon töötaks edukalt. Selle tööga seotud füüsikud olid hasartmängude suured fännid, nii et nad andsid simulatsioonidele koodnime Monte Carlo.
Järgmises viies peatükis näete näiteid selle kohta, kuidas kasutada Excelit Monte Carlo simulatsioonide tegemiseks.
Paljud ettevõtted kasutavad Monte Carlo simulatsiooni otsustusprotsessi olulise osana. Siin on mõned näited.
-
General Motors, Proctor ja Gamble, Pfizer, Bristol-Myers Squibb ja Eli Lilly kasutavad simulatsiooni, et hinnata nii uute toodete keskmist tasuvust kui ka riskitegurit. GM-i puhul kasutab tegevjuht seda teavet, et teha kindlaks, millised tooted turule jõuavad.
-
GM kasutab simulatsiooni sellisteks tegevusteks nagu ettevõtte puhastulu prognoosimine, struktuuri- ja ostukulude prognoosimine ning selle vastuvõtlikkuse määratlemine erinevate riskide suhtes (nt intressimäärade muutused ja vahetuskursi kõikumised).
-
Lilly kasutab simulatsiooni iga ravimi optimaalse taimevõimsuse määramiseks.
-
Proctor ja Gamble kasutavad simulatsiooni, et modelleerida ja optimaalselt riskida valuutariski.
-
Sears kasutab simulatsiooni, et teha kindlaks, kui palju iga tootesarja ühikut tuleks tarnijatelt tellida (nt Dockersi pükste paaride arv, mida tuleks tellida sel aastal).
-
Nafta- ja narkoettevõtted kasutavad simulatsiooni selleks, et hinnata "tegelikke võimalusi", näiteks projekti laiendamise, lepingu sõlmimise või edasilükkamise suvandi väärtust.
-
Finantsplaneerijad kasutavad Monte Carlo simulatsiooni, et määrata kindlaks klientide pensionile jäämise optimaalsed investeerimisstrateegiad.
Kui tipite lahtrisse valemi =RAND( ), saate arvu, mis tõenäoliselt eeldab suvalist väärtust vahemikus 0–1. Seega peaks umbes 25% ajast saama arvu, mis on väiksem või võrdne 0,25-ga; umbes 10% ajast peaksite saama arvu, mis on vähemalt 0,90 jne. Funktsiooni RAND tööpõhimõtete näitamiseks vaadake faili Randdemo.xlsx, mis on kujutatud joonisel 60–1.
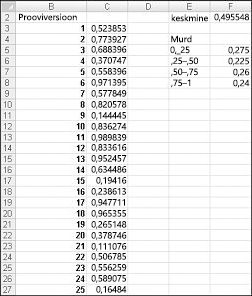
Märkus.: Kui avate faili Randdemo.xlsx, ei kuvata joonisel 60–1 kujutatud juhuslikke numbreid. Funktsioon RAND arvutab töölehe avamisel või töölehele uue teabe sisestamisel loodavad arvud alati automaatselt ümber.
Esmalt kopeerige lahtrist C3 lahtrisse C4:C402 valem =RAND(). Seejärel nimetate vahemiku C3:C402 Andmed. Seejärel saate veerus F jälgida 400 juhusliku arvu (lahtri F2) keskmist ja kasutada funktsiooni COUNTIF murrude määramiseks vahemikus 0–0,25, 0,25 kuni 0,50, 0,50 ja 0,75 ning 0,75 ja 1. Klahvi F9 vajutamisel arvutatakse juhuslikud arvud ümber. Pange tähele, et 400 arvu keskmine on alati ligikaudu 0,5 ja umbes 25% tulemustest on intervalliga 0,25. Need tulemused on kooskõlas juhusliku arvu määratlusega. Pange ka tähele, et funktsiooni RAND genereeritud väärtused on erinevates lahtrites sõltumatud. Näiteks kui lahtris C3 genereeritud juhuslik arv on suur arv (nt 0,99), ei räägi see meile teiste genereeritud juhuslike arvude väärtustest.
Oletagem, et kalendrinõudlust juhib järgmine eraldiseisev juhuslik muutuja:
|
Nõudlus |
Tõenäosus |
|
10 000 |
0,10 |
|
20 000 |
0.35 |
|
40,000 |
0,3 |
|
60 000 |
0,25 |
Kuidas saame lasta Excelil seda nõudlust kalendrite järele mitu korda esitada või jäljendada? Keerukas on siduda funktsiooni RAND iga võimalik väärtus kalendrite võimaliku nõudlusega. Järgmine ülesanne tagab, et 10 000 nõudlus tekib 10% ajast jne.
|
Nõudlus |
Määratud juhuarv |
|
10 000 |
Väiksem kui 0,10 |
|
20 000 |
Suurem kui 0,10 või sellega võrdne ja väiksem kui 0,45 |
|
40,000 |
Suurem kui 0,45 või sellega võrdne ja väiksem kui 0,75 |
|
60 000 |
Suurem kui 0,75 või sellega võrdne |
Nõudluse simulatsiooni demonstreerimiseks vaadake faili Discretesim.xlsx, mis on näidatud järgmisel lehel joonisel 60–2.
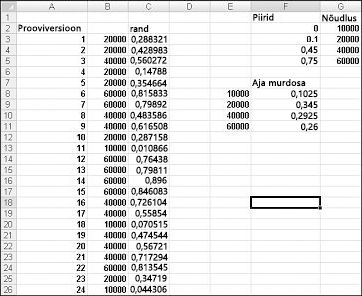
Simulatsiooni võti on kasutada juhuslikku arvu, et algatada otsing tabelivahemikust F2:G5 (nimega otsing). Juhuslikud arvud, mis on suuremad või võrdsed kui 0 ja väiksemad kui 0,10, annavad nõudluse 10 000; juhuslikud arvud, mis on suuremad või võrdsed kui 0,10 ja väiksemad kui 0,45, annavad nõudluse 20 000; juhuslikud arvud, mis on suuremad või võrdsed kui 0,45 ja väiksemad kui 0,75, annavad nõudluse 40 000; ja juhuslikud arvud, mis on suuremad kui 0,75 või sellega võrdsed, annavad nõudluse 60 000. 400 juhusliku arvu genereerimiseks kopeerite lahtrist C3 lahtrisse C4:C402 valemi RAND(). Seejärel genereerite kalendri nõudlusest 400 prooviversiooni ehk iteratsiooni, kopeerides valemi VLOOKUP(C3;otsing;2) lahtritest B3 lahtrisse B4:B402. See valem tagab, et suvaline juhuslik arv, mis on väiksem kui 0,10, tekitab nõudluse 10 000, suvaline juhuslik arv vahemikus 0,10–0,45 genereerib nõudluse 20 000 jne. Kasutage lahtrivahemikus F8:F11 funktsiooni COUNTIF, et määrata iga nõudlusele vastava 400 iteratsiooni murd. Kui vajutame juhuarvude ümberarvutamiseks klahvi F9, on jäljendatud tõenäosus meie eeldatavale nõudluse tõenäosusele lähedane.
Kui tipite mõnda lahtrisse valemi NORMINV(rand(),mu,sigma), loote jäljendatud väärtuse tavalisest juhuslikust muutujast, millel on keskväärtus mu ja standardhälve sigma. Seda protseduuri illustreerib Normalsim.xlsx joonisel 60–3 kujutatud joonisel 60–3.
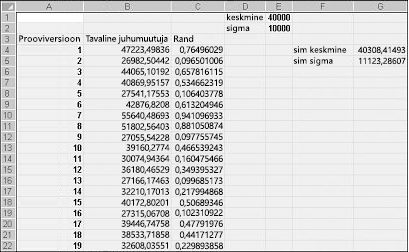
Oletame, et soovime simuleerida 400 katset ehk iteratsioone tavalise juhusliku muutuja jaoks keskväärtusega 40 000 ja standardhälbega 10 000. (Võite need väärtused tippida lahtritesse E1 ja E2 ning nimetada vastavalt nende lahtrite keskmise ja sigma.) Valemi =RAND() kopeerimisel lahtrist C4 lahtrisse C5:C403 luuakse 400 erinevat juhuslikku arvu. Kopeerides lahtrist B4 lahtrisse B5:B403, genereerib valem NORMINV(C4;keskväärtus;sigma) tavalisest juhuslikust muutujast 40 000 erineva prooviväärtuse ja standardhälbega 10 000. Kui vajutame juhuslike arvude ümberarvutamiseks klahvi F9, jääb keskmine 40 000-le ja standardhälve 10 000-le lähemale.
Sisuliselt genereerib valem NORMINV(p,mu,sigma) juhusliku normaalmuutuja p-protsentiilikeskväärtusega mu ja standardhälbe sigmaga. Näiteks juhuarv 0,77 lahtris C4 (vt joonis 60–3) genereerib lahtris B4 ligikaudu tavalise juhusliku muutuja 77. protsentiil keskmisega 40 000 ja standardhälbega 10 000.
Selles jaotises näete, kuidas Monte Carlo simulatsiooni saab kasutada otsustamise tööriistana. Oletagem, et nõudlus sõbrapäevakaardi järele on reguleeritud järgmise diskreetse juhusliku muutujaga:
|
Nõudlus |
Tõenäosus |
|
10 000 |
0,10 |
|
20 000 |
0.35 |
|
40,000 |
0,3 |
|
60 000 |
0,25 |
Tervituskaart müüb 4,00 $ eest ja iga kaardi tootmise muutuv hind on 1,50 $. Ülejäägikaardid tuleb likvideerida hinnaga 0,20 eurot kaardi kohta. Mitu kaarti tuleks printida?
Põhimõtteliselt simuleerime iga võimalikku tootmiskogust (10 000, 20 000, 40 000 või 60 000) mitu korda (nt 1000 iteratsiooni). Seejärel määratleme, milline tellimuse kogus annab maksimaalse keskmise kasumi 1000 iteratsiooni kohta. Selle jaotise andmed leiate joonisel 60–4 kujutatud faili Valentine.xlsx. Lahtrites B1:B11 olevate vahemikunimede määramiseks lahtritele C1:C11. Lahtrivahemikule G3:H6 määratakse nimeotsimine. Meie müügihinna ja kulu parameetrid sisestatakse lahtritesse C4:C6.
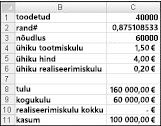
Proovitootmise koguse (selles näites 40 000) saate sisestada lahtrisse C1. Järgmiseks looge lahtris C2 juhuarv valemiga =RAND(). Nagu eespool kirjeldatud, simuleerite lahtris C3 asuva kaardi nõudlust valemiga VLOOKUP(rand,lookup,2). (Funktsiooni VLOOKUP valemis on rand lahtrile C3 määratud lahtrinimi, mitte funktsioon RAND.)
Müüdud ühikute arv on väiksem meie toodangu kogusest ja nõudlusest. Lahtris C8 arvutate meie tulu valemiga MIN(toodetud,nõudlus)*unit_price. Lahtris C9 arvutatakse tootmiskulu kokku valemiga , mis on toodetud*unit_prod_cost.
Kui toodame rohkem kaarte kui nõudmisel, võrdub ülejäänud ühikute arv tootmisel miinus nõudlus; vastasel juhul ei jää ühtegi üksust üle. Arvutame lahtris C10 kõrvaldamismaksumuse valemiga unit_disp_cost*IF(toodetud>nõudlus,toodetud–nõudlus;0). Lõpuks arvutame lahtris C11 oma kasumi tuluna – total_var_cost-total_disposing_cost.
Soovime tõhusat viisi klahvi F9 vajutamiseks mitu korda (nt 1000) iga tootmiskoguse kohta ja tagada iga koguse oodatav kasum. Selline olukord on selline, kus tuleb appi kahesuunaline andmetabel. (Lisateavet andmetabelite kohta leiate peatükist 15 "Tundlikkusanalüüs andmetabelitega". Selles näites kasutatav andmetabel on kujutatud joonisel 60–5.
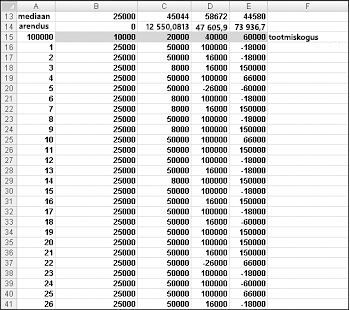
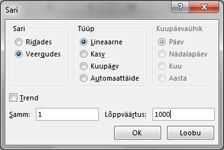
Sisestage lahtrivahemikku A16:A1015 arvud 1–1000 (vastab meie 1000 prooviversioonile). Üks lihtne viis nende väärtuste loomiseks on alustada lahtrisse A16 1 sisestamisega. Valige lahter ja seejärel klõpsake menüü Avaleht jaotises Redigeerimine nuppu Täide ja valige dialoogiboksi Sari kuvamiseks Sari . Sisestage dialoogiboksi Sari joonisel 60–6 kuvatud dialoogiboksis Sari etapi väärtus 1 ja stopp-väärtus 1000. Valige jaotises Sarjade arv suvand Veerud ja seejärel klõpsake nuppu OK. Arvud 1–1000 sisestatakse veergu A alates lahtrist A16.
Järgmiseks sisestame lahtritesse B15:E15 oma võimalikud tootmiskogused (10 000, 20 000, 40 000, 60 000). Soovime arvutada kasumi iga prooviversiooni numbri (1 kuni 1000) ja iga tootmiskoguse kohta. Viitame kasumivalemile (arvutatud lahtris C11) meie andmetabeli ülemises vasakpoolses lahtris (A15), sisestades =C11.
Nüüd oleme valmis Excelit meelitama simuleerima 1000 nõudluse iteratsiooni iga tootmiskoguse kohta. Valige tabelivahemik (A15:E1014) ja seejärel klõpsake menüü Andmed jaotises Andmeriistad nuppu What If Analysis (Mõjuanalüüs) ja seejärel valige Data Table (Andmetabel). Kahesuunalise andmetabeli häälestamiseks valige reasisestuslahtriks oma tootmiskogus (lahter C1) ja valige veerusisestuslahtriks mis tahes tühi lahter (valisime lahtri I14). Pärast nupu OK klõpsamist simuleerib Excel iga tellimuse koguse jaoks 1000 nõudluse väärtust.
Selle toimimise mõistmiseks kaaluge andmetabeli paigutatud väärtusi lahtrivahemikus C16:C1015. Iga lahtri puhul kasutab Excel lahtris C1 väärtust 20 000. Lahtris C16 paigutatakse veeru sisendlahtri väärtus 1 tühja lahtrisse ja juhuslik arv lahtris C2 arvutatakse ümber. Vastav kasum registreeritakse seejärel lahtris C16. Seejärel paigutatakse veerulahtri sisendväärtus 2 tühja lahtrisse ja lahtris C2 olev juhuslik arv arvutatakse uuesti. Vastav kasum sisestatakse lahtrisse C17.
Kopeerides lahtrist B13 lahtrisse C13:E13 valemi AVERAGE(B16:B1015), arvutame iga tootmiskoguse kohta jäljendatud keskmise kasumi. Kopeerides lahtrist B14 lahtrisse C14:E14 valemi STDEV(B16:B1015), arvutame iga tellimuse koguse kohta simuleeritud kasumi standardhälbe. Iga kord, kui vajutame klahvi F9, simuleeritakse iga tellimuse koguse kohta 1000 nõudluse iteratsiooni. 40 000 kaardi tootmine annab alati suurima eeldatava kasumi. Seetõttu näib, et 40 000 kaardi valmistamine on õige otsus.
Riski mõju meie otsusele Kui tootsime 40 000 kaardi asemel 20 000 kaarti, siis meie eeldatav kasum langeb umbes 22 protsenti, kuid meie risk (mõõdetuna kasumi standardhälbega) langeb peaaegu 73 protsenti. Seega, kui me oleme äärmiselt pöördelised riskima, võib õige otsuse langetada 20 000 kaarti. Muide, 10 000 kaartide tootmisel on standardhälve 0 kaarti, sest kui me toodame 10 000 kaarti, müüme alati kõiki neid ilma ülejääkideta.
Märkus.: Selles töövihikus on suvandi Arvutus väärtuseks seatud Automaatne, v.a tabelite puhul. (Kasutage menüü Valemid jaotise Arvutamine käsku Arvutamine.) See säte tagab, et meie andmetabelit ei arvutata ümber enne, kui vajutame klahvi F9. See on hea mõte, kuna mahukas andmetabel aeglustab teie tööd, kui see arvutatakse ümber iga kord, kui tipite midagi oma töölehele. Pange tähele, et selles näites muutub keskmine kasum iga kord, kui vajutate klahvi F9. Põhjus on selles, et iga kord, kui vajutate klahvi F9, kasutatakse iga tellimuse koguse jaoks nõudluse genereerimiseks erinevat 1000 juhuslikku arvu järjestust.
Keskmise kasumi usaldusvahemik Loomulik küsimus, mida selles olukorras esitada, on, millise intervalliga oleme 95 protsenti kindlad, et tegelik keskmine kasum langeb? Seda intervalli nimetatakse keskmise kasumi 95-protsendiliseks usaldusvahemikuks. Simulatsiooniväljundi keskmise 95-protsendiline usaldusvahemik arvutatakse järgmise valemiga:
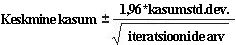
Lahtris J11 arvutate keskmise kasumi 95-protsendilise usaldusvahemiku alampiiri, kui valemiga D13–1,96*D14/SQRT(1000) luuakse 40 000 kalendrit. Lahtris J12 arvutate meie 95-protsendilise usaldusvahemiku ülempiiri valemiga D13+1,96*D14/SQRT(1000). Need arvutused on esitatud joonisel 60–7.
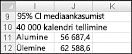
Oleme 95% kindlad, et meie keskmine kasum 40 000 kalendri tellimisel on vahemikus 56 687 kuni 62 589 $.
-
GMC edasimüüja usub, et nõudlus 2005. Tema saadiku vastuvõtmise hind on 25 000 dollarit ja ta müüb saadiku 40 000 dollari eest. Pool kõigist saadikutest, kes ei ole täishinnaga müüdud, saab müüa 30 000 dollari eest. Ta kaalub 200, 220, 240, 260, 280 või 300 saadiku tellimist. Kui palju ta peaks tellima?
-
Väike supermarket püüab kindlaks teha, mitu Inimesed ajakirja koopiat nad peaksid iga nädal tellima. Nad usuvad, et nende nõudlust Inimesed reguleerib järgmine eraldiseisev juhuslik muutuja:
Nõudlus
Tõenäosus
15
0,10
20
0.20
25
0.30
30
0,25
35
0,15
-
Supermarket maksab iga Inimesed eksemplari eest 1,00 $ ja müüb selle 1,95 dollari eest. Iga müümata koopia saab tagastada 0,50 dollari eest. Mitu Inimesed eksemplari tuleks poes tellida?
Kas vajate rohkem abi?
Kui teil on küsimusi, saate need esitada Exceli tehnikakogukonnafoorumis, kus teile vastavad asjatundjad, või teistele kasutajatele kogukonnafoorumis.










