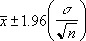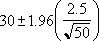הפונקציה מחזירה את הרווח בר-הסמך עבור ממוצע אוכלוסיה עם התפלגות נורמלית. הרווח בר-הסמך הוא טווח בכל צד של ממוצע מדגם. לדוגמה, אם אתה מציין אם הזמנת מוצר בדואר, תוכל לקבוע, ברמת מהימנות מסוימת, המועד המוקדם ביותר והתאריך המאוחר ביותר שבו המוצר יגיע.
תחביר
CONFIDENCE(alpha,standard_dev,size)
Alpha היא רמת המובהקות המשמשת לחישוב רמת הביטחון. רמת הביטחון שווה ל- 100*(1 - alpha)%, או במילים אחרות, alpha של 0.05 מציין רמת ביטחון של 95 אחוז.
Standard_dev הוא סטיית התקן של האוכלוסיה עבור טווח הנתונים וההנחה היא כי הוא ידוע.
גודל הוא גודל המדגם.
הערות
-
אם ארגומנט כלשהו אינו מספרי, הפונקציה CONFIDENCE מחזירה את ערך #VALUE! ערך שגיאה.
-
אם alpha ≤ 0 או alpha ≥ 1, הפונקציה CONFIDENCE מחזירה את #NUM! ערך שגיאה.
-
אם standard_dev ≤ 0, הפונקציה CONFIDENCE מחזירה את #NUM! ערך שגיאה.
-
אם הגודל אינו מספר שלם, הוא נחתך.
-
אם size < 1, הפונקציה CONFIDENCE מחזירה את #NUM! ערך שגיאה.
-
אם נניח כי alpha שווה 0.05, עלינו לחשב את השטח הנמצא מתחת לעקומה הסטנדרטית הנורמלית השווה ל- (1 - alpha), או 95 אחוזים. ערך זה הוא 1.96 ±. לפיכך, הרווח בר-הסמך הוא:
דוגמה
נניח שנבחין כי במדגם שלנו של 50 נסיעות, אורך הנסיעה הממוצע לעבודה הוא 30 דקות עם סטיית תקן של אוכלוסיה של 2.5. אנו יכולים להיות בטוחים ב- 95% שמ ממוצע האוכלוסיה נמצא במרווח הזמן:
|
Alpha |
סטיית יציבות |
גודל |
נוסחה |
תיאור (תוצאה) |
|---|---|---|---|---|
|
0.05 |
.5 |
50 |
=CONFIDENCE([Alpha],[StdDev],[Size]) |
רווח בר-סמך עבור ממוצע אוכלוסיה. במילים אחרות, אורך הנסיעה הממוצע לעבודה שווה ל- 30 ± 0.692951 דקות, או 29.3 עד 30.7 דקות. (0.692951) |