חשוב: התמיכה ב- Excel 2016 ו- Excel 2019 הסתיימה ב- 14 באוקטובר 2025. שדרג ל- Microsoft 365 כדי לעבוד מכל מקום ומכל מכשיר ולהמשיך ולקבל תמיכה. השג את Microsoft 365
מאמר זה דן בשימוש ב- Solver, תוכנית תוספת של Microsoft Excel שניתן להשתמש בה לניתוח 'מה-אם', כדי לקבוע שילוב מיטבי של מוצרים.
כיצד אוכל לקבוע את שילוב המוצר החודשי שמגדיל את הרווחיות?
חברות צריכות לעתים קרובות לקבוע את כמות המוצרים שברצונך להפיק על בסיס חודשי. בצורתו הפשוטה ביותר, בעיית שילוב המוצר כרוכה בכיצד לקבוע את הכמות של כל מוצר שיש ליצור במהלך חודש כדי להגדיל את הרווחים. שילוב המוצר חייב בדרך כלל לציית לאילוצים הבאים:
-
ל- Product mix אין אפשרות להשתמש במשאבים נוספים מההמשאבים הזמינים.
-
לכל מוצר יש דרישה מוגבלת. אנחנו לא יכולים להפיק יותר של מוצר במהלך חודש מאשר הביקוש מכתיב, כי ייצור עודף הוא מבוזבז (לדוגמה, תרופה מתישה).
כעת נפתור את הדוגמה הבאה של בעיית שילוב המוצר. ניתן למצוא את הפתרון לבעיה זו בקובץ Prodmix.xlsx, המוצג באיור 27-1.
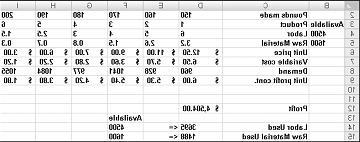
נניח שאנחנו עובדים עבור חברת תרופות המפיקה שישה מוצרים שונים במפעל שלהם. הפקה של כל מוצר דורשת עבודה וחומר גלם. שורה 4 באיור 27-1 מציגה את שעות העבודה הדרושות כדי לייצר קילו של כל מוצר, ושורה 5 מציגה את פאונדים של חומר גלם הדרושים כדי לייצר קילוגרם של כל מוצר. לדוגמה, הפקת פאונד של מוצר 1 דורשת שש שעות עבודה ו- 3.2 פאונד של חומר גולמי. עבור כל תרופה, המחיר לכל פאונד ניתן בשורה 6, העלות ליחידה לכל פאונד נתונה בשורה 7, והתרומה הרווחית לכל פאונד נתונה בשורה 9. לדוגמה, מוצר 2 מוכר ב- $11.00 לכל פאונד, כרוך בעלות יחידה של $5.70 לכל פאונד, ותורם רווח של $5.30 לכל פאונד. הדרישה של החודש עבור כל תרופה נתונה בשורה 8. לדוגמה, הביקוש עבור מוצר 3 הוא 1041 פאונד. החודש, 4500 שעות עבודה ו 1600 ק"ג של חומר גולמי זמינים. כיצד יכולה החברה למקסם את הרווח החודשי שלה?
אם לא היינו יודעים דבר על Excel Solver, היינו תוקפים בעיה זו על-ידי בניית גליון עבודה למעקב אחר רווח ושימוש במשאבים המשויכים לשילוב המוצר. לאחר מכן נשתמש בגירסת ניסיון ובשגיאה כדי לשנות את שילוב המוצר כדי למטב את הרווח מבלי להשתמש ביותר חומרי עבודה או חומר גולמי מאשר זמין, וללא צורך בהפקת תרופות מיותרות מביקוש. אנו משתמשים ב- Solver בתהליך זה רק בשלב הניסיון והשגיאה. למעשה, Solver הוא מנגנון מיטוב המבצע ללא פגמים את חיפוש הניסיון והשגיאה.
מפתח לפתרון בעיית שילוב המוצר הוא לחשב ביעילות את השימוש במשאבים והרווח המשויכים לכל שילוב מוצר נתון. כלי חשוב שנוכל להשתמש בו כדי להפוך חישוב זה לפונקציה SUMPRODUCT זו. הפונקציה SUMPRODUCT מכפילה ערכים תואמים בטווחי תאים ומחזירה את סכום הערכים הללו. לכל טווח תאים המשמש בהערכת SUMPRODUCT חייב להיות ממדים זהים, מה שמציין שניתן להשתמש ב- SUMPRODUCT עם שתי שורות או שתי עמודות, אך לא עם עמודה אחת ושורה אחת.
כדוגמה לאופן שבו נוכל להשתמש בפונקציה SUMPRODUCT במוצר שלנו, ננסה לחשב את השימוש במשאבים שלנו. השימוש שלנו בעבודה מחושב על-ידי
(העבודה בשימוש לכל קילו של סמים 1)*(תרופות 1 פאונד מופק)+ (העבודה בשימוש לכל קילו של תרופות 2)*(תרופות 2 פאונד מופק) + ... (העבודה בשימוש לכל קילו של סמים 6)*(תרופות שהופקו 6 פאונד)
נוכל לחשב את השימוש בעבודה בצורה מעיה יותר כמו D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. באופן דומה, ניתן לחשב שימוש בחומר גולמי כ- D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. עם זאת, הזנת נוסחאות אלה בגליון עבודה עבור שישה מוצרים צורכת זמן רב. דמיין כמה זמן ייקח אם אתה עובד עם חברה שמייצרת, לדוגמה, 50 מוצרים במפעל שלהם. דרך קלה הרבה יותר לחשב עבודה ושימוש בחומר גולמי היא להעתיק מ- D14 ל- D15 את הנוסחה SUMPRODUCT($D$2:$I$2,D4:I4). נוסחה זו מחשבת את D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (שהוא השימוש שלנו בעבודה), אך קל הרבה יותר להזין אותו! שים לב כי אני משתמש בסימן $ עם הטווח D2:I2 כך כשאני מעתיק את הנוסחה אני עדיין לוכד את שילוב המוצר משורה 2. הנוסחה בתא D15 מחשבת שימוש בחומר גולמי.
באופן דומה, הרווח שלנו נקבע על-ידי
(רווח מסמים 1 לכל פאונד)*(תרופות 1 פאונד מופק) + (סמים 2 רווח לכל פאונד)*(תרופות 2 פאונד מופק) + ... (סמים 6 רווח לכל פאונד)*(תרופות 6 פאונד מופק)
הרווח מחושב בקלות בתא D12 באמצעות הנוסחה SUMPRODUCT(D9:I9,$D$2:$I$2).
כעת ניתן לזהות את שלושת הרכיבים של מודל Solver של שילוב המוצר שלנו.
-
תא יעד. המטרה שלנו היא להגדיל את הרווחים (מחושב בתא D12).
-
תאים משתנים. מספר פאונדים המופקים של כל מוצר (מפורט בטווח התאים D2:I2)
-
אילוצים. יש לנו את האילוצים הבאים:
-
אין להשתמש ביותר חומרי עבודה או חומר גולמי מאשר זמין. לדוגמה, הערכים בתאים D14:D15 (המשאבים שבהם נעשה שימוש) חייבים להיות קטנים או שווים לערכים בתאים F14:F15 (המשאבים הזמינים).
-
אין לייצר יותר של תרופה מאשר מבוקש. כלומר, הערכים בתאים D2:I2 (פאונדים המופקים מכל תרופה) חייבים להיות קטנים או שווים לביקוש עבור כל תרופה (המפורטים בתאים D8:I8).
-
אנחנו לא יכולים לייצר סכום שלילי של כל תרופה.
-
אני אראה לך כיצד להזין את תא היעד, לשנות תאים ואילוצים ל- Solver. לאחר מכן כל שעליך לעשות הוא ללחוץ על לחצן פתור כדי למצוא שילוב מוצר להגדלת הרווח!
כדי להתחיל, לחץ על הכרטיסיה נתונים, ובקבוצה ניתוח, לחץ על Solver.
הערה: כפי שמוסבר בפרק 26, "מבוא למיטוב עם Excel Solver", Solver מותקן על-ידי לחיצה על לחצן Microsoft Office, לאחר מכן אפשרויות Excel ואחריו תוספות. ברשימה ניהול, לחץ על תוספות של Excel, סמן את התיבה Solver Add-in ולאחר מכן לחץ על אישור.
תיבת הדו-שיח Solver Parameters תופיע, כפי שמוצג באיור 27-2.
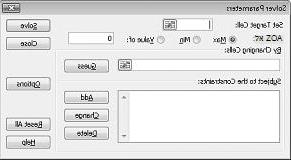
לחץ על התיבה הגדר תא יעד ולאחר מכן בחר את תא הרווח שלנו (תא D12). לחץ על התיבה לפי תאים משתנים ולאחר מכן הצבע על הטווח D2:I2, המכיל את פאונדים שיוצרו של כל תרופה. תיבת הדו-שיח אמורה להיראות כעת באיור 27-3.
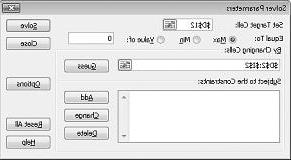
כעת אנחנו מוכנים להוסיף אילוצים למודל. לחץ על לחצן הוסף. תראה את תיבת הדו-שיח הוספת אילוץ, המוצגת באיור 27-4.
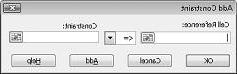
כדי להוסיף את אילוצי השימוש במשאבים, לחץ על התיבה הפניה לתא ולאחר מכן בחר את הטווח D14:D15. בחר <= מהרשימה האמצעית. לחץ על התיבה אילוץ ולאחר מכן בחר את טווח התאים F14:F15. תיבת הדו-שיח הוספת אילוץ אמורה להיראות כעת כמו איור 27-5.
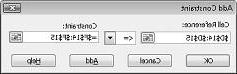
כעת וודאנו כי כאשר Solver ינסה ערכים שונים עבור התאים המשתנים, ייחשבו רק שילובים התואמים הן את D14<=F14 (העבודה שנמצאת בשימוש נמוכה או שווה לעבודה) והן D15<=F15 (חומר גולמי שנמצא בשימוש קטן או שווה חומר גולמי זמין). לחץ על הוסף כדי להזין את אילוצי הביקוש. מלא את תיבת הדו-שיח הוספת אילוץ כפי שמוצג באיור 27-6.
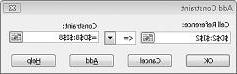
הוספת אילוצים אלה מבטיחה כי כאשר Solver ינסה שילובים שונים עבור ערכי התאים המשתנים, ייחשבו רק שילובים הממלאים את הפרמטרים הבאים:
-
D2<=D8 (הסכום המיוצר מסמים 1 קטן או שווה לביקוש עבור סמים 1)
-
E2<=E8 (כמות המיוצרת של סמים 2 היא קטנה או שווה לביקוש עבור סמים 2)
-
F2<=F8 (הסכום המיוצר מסמים 3 נעשה קטן או שווה לביקוש עבור סמים 3)
-
G2<=G8 (הסכום שנוצר מסמים 4 הוא קטן או שווה לביקוש עבור סמים 4)
-
H2<=H8 (הכמות המיוצרת מסמים 5 made is less than or equal to the demand for Drug 5)
-
I2<=I8 (הסכום המיוצר מסמים 6 הוא פחות או שווה לביקוש עבור סמים 6)
לחץ על אישור בתיבת הדו-שיח הוספת אילוץ. החלון Solver אמור להיראות כמו איור 27-7.
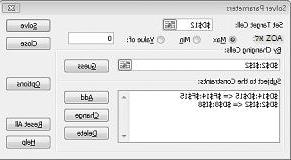
אנו להזין את האילוץ שהתאים המשתנים חייבים להיות לא שליליים בתיבת הדו-שיח אפשרויות Solver. לחץ על לחצן אפשרויות בתיבת הדו-שיח Solver Parameters. סמן את התיבה נניח מודל ליניארי ואת התיבה נניח שאינו שלילי, כפי שמוצג באיור 27-8 בעמוד הבא. לחץ על 'אישור'.
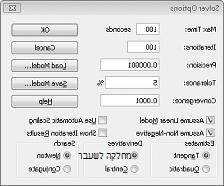
סימון התיבה 'נניח שאינו שלילי' מבטיחה ש- Solver מתחשב רק בשילובים של תאים משתנים שבהם כל תא משתנה מניח ערך לא שלילי. בדקנו את התיבה 'נניח מודל ליניארי' מאחר שבעיית שילוב המוצר היא סוג מיוחד של בעיית Solver הנקראת מודל ליניארי. למעשה, מודל Solver הוא ליניארי בתנאים הבאים:
-
תא היעד מחושב על-ידי הוספת מונחי הטופס (התא המשתנים)*(קבוע).
-
כל אילוץ עומדת ב"דרישת המודל הליניארי". משמעות הדבר היא שכל אילוץ מוערך על-ידי הוספת מונחי הטופס (שינוי תא )*(קבוע) והשוואה בין הסכום לקבוע.
מדוע בעיית Solver זו ליניאארית? תא היעד (רווח) שלנו מחושב כ
(רווח מסמים 1 לכל פאונד)*(תרופות 1 פאונד מופק) + (סמים 2 רווח לכל פאונד)*(תרופות 2 פאונד מופק) + ... (סמים 6 רווח לכל פאונד)*(תרופות 6 פאונד מופק)
חישוב זה עוקב אחר תבנית שבה הערך של תא היעד נגזר על-ידי הוספת מונחים של הטופס (שינוי תא)*(קבוע).
אילוץ העבודה שלנו מוערך על ידי השוואת הערך הנגזר (העבודה בשימוש לכל פאונד של תרופות 1)*(תרופות 1 פאונד המופק) + (העבודה בשימוש לכל פאונד של סמים 2)*(תרופות 2 פאונד המופק)+ ... (עמים)ed לכל קילו של סמים 6)*(תרופות 6 פאונד מופק) לעבודה זמינה.
לכן, אילוץ העבודה מוערך על-ידי חיבור מונחי הטופס (שינוי תא )*(קבוע) והשוואה בין הסכום לקבוע. אילוץ העבודה ואילוץ החומר הגולמי ממלאים את דרישת המודל הליניארי.
אילוצי הביקוש שלנו מופיעים בתבנית
(תרופות 1 מופק)<=(סמים 1 דרישה) (תרופות 2 מופק)<=(סמים 2 דרישה) ₪(תרופות 6 מופק)<=(סמים 6 דרישה)
כל אילוץ ביקוש גם עונה על דרישת המודל הליניארי, מכיוון שכל אחד מהם מוערך על-ידי הוספת מונחי הטופס (שינוי תא )*(קבוע) והשוואה בין הסכומי לקבוע.
לאחר שהצגנו שהמודל שלנו לשילוב מוצרים הוא מודל ליניארי, למה אכפת לנו?
-
אם מודל Solver הוא ליניארי ואנחנו בוחרים בהנחה שמודל ליניארי, Solver מובטח למצוא את הפתרון האופטימלי למודל Solver. אם מודל Solver אינו ליניארי, Solver עשוי למצוא או לא למצוא את הפתרון האופטימלי.
-
אם מודל Solver הוא ליניארי ואנחנו בוחרים בהנחה שמודל ליניארי, Solver משתמש באלגוריתם יעיל מאוד (שיטת simplex) כדי למצוא את הפתרון האופטימלי של המודל. אם מודל Solver הוא ליניארי ולא נבחר בהנחה שמודל ליניארי, Solver משתמש באלגוריתם לא יעיל מאוד (שיטת GRG2) וייתכן שהוא מתקשה למצוא את הפתרון האופטימלי של המודל.
לאחר לחיצה על אישור בתיבת הדו-שיח אפשרויות Solver, אנו לחזור לתיבת הדו-שיח הראשית Solver, המוצגת קודם לכן באיור 27-7. כאשר אנו לוחץים על Solve, Solver מחשב פתרון מיטבי (אם קיים) עבור מודל שילוב המוצר שלנו. כפי שציינתי בפרק 26, פתרון מיטבי למודל שילוב המוצר יהיה קבוצה של ערכי תאים משתנים (פאונד המופקים מכל תרופה) שמגדילה את הרווח מעל כל הפתרונות האפשריים. שוב, פתרון ישים הוא ערכה של ערכי תאים משתנים המספקים את כל האילוצים. ערכי התאים המשתנים המוצגים באיור 27-9 הם פתרון ישים מאחר שכל רמות הייצור אינן שליליות, רמות ייצור אינן חורגות מהביקוש, ושימוש במשאבים אינו חורג מהמשאבים הזמינים.
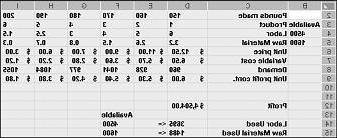
ערכי התאים המשתנים המוצגים באיור 27-10 בעמוד הבא מייצגים פתרון בלתי נגיש מהסיבות הבאות:
-
אנחנו מייצרים יותר של סמים 5 מהביקוש עבורה.
-
אנו משתמשים ביותר עבודה ממה שזמין.
-
אנו משתמשים ביותר חומר גולמי ממה הזמין.
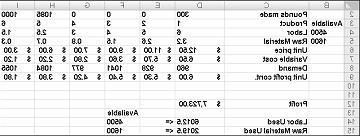
לאחר לחיצה על Solve, Solver מוצא במהירות את הפתרון האופטימלי המוצג באיור 27-11. עליך לבחור באפשרות שמור פתרון Solver כדי לשמר את ערכי הפתרון האופטימליים בגליון העבודה.
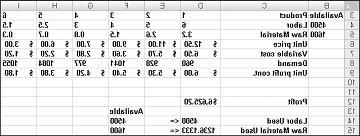
חברת התרופות שלנו יכולה להגדיל את הרווח החודשי שלה ברמה של $6,625.20 על ידי הפקת 596.67 פאונדים של סמים 4, 1084 קילוגרמים של סמים 5, ו אף אחד הסמים האחרים! איננו יכולים לקבוע אם נוכל להשיג את הרווח המרבי של $6,625.20 בדרכים אחרות. כל מה שאנחנו יכולים להיות בטוחים הוא שבהמשאבים והביקוש המוגבלת שלנו, אין דרך לעשות יותר מ- $6,627.20 החודש.
נניח שיש לספק דרישה זו עבור כל מוצר. (עיין בגליון העבודה 'ללא פתרון ניתן להמרה' בקובץ Prodmix.xlsx). לאחר מכן עלינו לשנות את אילוצי הביקוש שלנו מ- D2:I2<=D8:I8 ל- D2:I2>=D8:I8. לשם כך, פתח את Solver, בחר את האילוץ D2:I2<=D8:I8 ולאחר מכן לחץ על שנה. תיבת הדו-שיח שינוי אילוץ, המוצגת באיור 27-12, מופיעה.
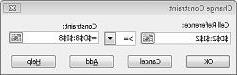
בחר >=, ולאחר מכן לחץ על אישור. כעת וודאנו ש- Solver ישקול לשנות רק ערכי תאים העומדים בכל הדרישות. כאשר תלחץ על פתור, תראה את ההודעה "ל- Solver לא היתה אפשרות למצוא פתרון ישים". הודעה זו אינה אומרת שעשינו טעות במודל שלנו, אך במקום זאת, עם המשאבים המוגבלת שלנו, לא נוכל לעמוד בביקוש עבור כל המוצרים. Solver פשוט אומר לנו שאם אנחנו רוצים לעמוד בביקוש עבור כל מוצר, עלינו להוסיף עוד חומרי עבודה, חומרי גלם נוספים או יותר משניהם.
בוא נראה מה קורה אם אנו מאפשרים דרישה בלתי מוגבלת עבור כל מוצר, ואנו מאפשרים הפקה של כמויות שליליות של כל תרופה. (ניתן לראות בעיה זו של Solver בגליון העבודה Set Values Do Not Converge בקובץ Prodmix.xlsx.) כדי למצוא את הפתרון האופטימלי למצב זה, פתח את Solver, לחץ על לחצן אפשרויות ונקה את התיבה נניח כלא שלילי. בתיבת הדו-שיח Solver Parameters, בחר את אילוץ הביקוש D2:I2<=D8:I8 ולאחר מכן לחץ על Delete כדי להסיר את האילוץ. בעת לחיצה על Solve, Solver מחזיר את ההודעה "Set Cell Values Do Not Converge". הודעה זו פירושה שאם תא היעד יהיה מוגדל (כמו בדוגמה שלנו), קיימים פתרונות אפשריים עם ערכי תא יעד גדולים שרירותיים. (אם תא היעד ממוזער, ההודעה "הגדר ערכי תא אל תשוחח" פירושה שקיימים פתרונות אפשריים עם ערכי תא יעד קטנים שרירותיים.) במצבנו, על-ידי מתן אפשרות לייצור תרופה שלילית, אנו בתוקף "יוצרים" משאבים שניתן להשתמש בהם כדי לייצר כמויות גדולות באופן שרירותי של תרופות אחרות. בהתחשב בביקוש הבלתי מוגבל שלנו, זה מאפשר לנו להרוויח ללא הגבלה. במצב ממשי, אנחנו לא יכולים לעשות סכום אינסופי של כסף. בהיקף קצר, אם אתה רואה את הטקסט "Set Values Do Not Converge", קיימת שגיאה במודל שלך.
-
נניח ש חברת התרופות שלנו יכולה לרכוש עד 500 שעות עבודה ב- $1 יותר לשעה מאשר עלויות העבודה הנוכחיות. כיצד נוכל להגדיל את הרווחים?
-
במפעל לייצור שבבים, ארבעה טכנאים (A, B, C ו- D) מייצרים שלושה מוצרים (מוצרים 1, 2 ו- 3). החודש, יצרן השבבים יכול למכור 80 יחידות של מוצר 1, 50 יחידות של מוצר 2, ולרוב 50 יחידות של מוצר 3. טכנאי א' יכול להפוך רק את המוצרים 1 ו- 3. טכנאי ב' יכול ליצור רק מוצרים 1 ו- 2. טכנאי ג' יכול להפוך למוצר 3 בלבד. טכנאי ד' יכול להפוך למוצר 2 בלבד. עבור כל יחידה המופקת, המוצרים תורמים את הרווח הבא: מוצר 1, $6; מוצר 2, $7; ומוצר 3, $10. השעה (בשעות) שכל טכנאי צריך לייצר מוצר הוא כדלקמן:
מוצר
טכנאי א'
טכנאי ב
טכנאי ג'
טכנאי ד
1
2
2.5
אין אפשרות לבצע
אין אפשרות לבצע
2
אין אפשרות לבצע
3
אין אפשרות לבצע
3.5
3
3
אין אפשרות לבצע
4
אין אפשרות לבצע
-
כל טכנאי יכול לעבוד עד 120 שעות בחודש. כיצד יצרן השבב יכול למקסם את הרווח החודשי שלו? נניח שניתן ליצור מספר שבר של יחידות.
-
מפעל לייצור מחשבים מייצר עכברים, מקלדות ו מוטות ג'ויסטיק של משחקי וידאו. הטבלה הבאה תינתן בטבלה הבאה רווח לפי יחידה, שימוש בכל יחידה לעבודה, דרישה חודשית ושימוש בזמן מכונה ליחידה:
עכברים
מקלדות
ג'ויסטיקים
רווח/יחידה
400 $ מחיר
100 $ מחיר
200 $
שימוש בעבודה/יחידה
.2 שעה
.3 שעה
.24 שעות
זמן/יחידה של מחשב
.04 שעה
.055 שעה
.04 שעה
דרישה חודשית
15,000
27,000
11,000
-
בכל חודש, זמינים בסך הכל 13,000 שעות עבודה ו- 3,000 שעות של זמן מכונה. כיצד יכול היצרן למקסם את תרומה הרווח החודשית שלו מהצמח?
-
פתור את דוגמת התרופה שלנו בהנחה שיש לספק דרישה מינימלית של 200 יחידות עבור כל תרופה.
-
ג'ייסון יוצר צמידי יהלומים, שרשראות ועגילים. הוא רוצה לעבוד עד 160 שעות בחודש. יש לו 800 אונקיות של יהלומים. הרווח, זמן העבודה, אונקיות של יהלומים הנדרשים כדי לייצר כל מוצר ניתן להלן. אם הביקוש עבור כל מוצר הוא בלתי מוגבל, כיצד ג'ייסון יכול להגדיל את הרווח שלו?
מוצר
רווח יחידה
שעות עבודה ליחידה
אונקיות יהלומים ליחידה
צמיד
$300
.35
1.2
שרשרת
₪200
.15
.75
עגילים
$100
.05
.5










