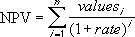NPV (opis funkcije)

Sintaksa

NPV(stopa;vrijednost1;vrijednost2;...)

Stopa     je diskontna stopa tijekom jednog razdoblja.

Vrijednost1, vrijednost2,...     od 1 do 29 argumenata koji predstavljaju plaćanja i prihode. Vrijednost1, vrijednost2,... moraju biti jednako razmakni u vremenu i pojaviti se na kraju svakog razdoblja. NPV koristi redoslijed vrijednosti1, vrijednost2,... za tumačenje redoslijeda novčanih tokova. Provjerite jeste li vrijednosti novčanih izdataka i primitaka unijeli ispravnim redoslijedom. Broje se argumenti koji su brojevi, prazni, logičke vrijednosti ili tekstni prikazi brojeva; argumenti koji su vrijednosti pogreške ili tekst koji se ne mogu prevesti u brojeve zanemaruju se.

Napomene

• NPV ulaganje započinje jedno razdoblje prije datuma prvog novčanog toka izraženog argumentom vrijednost1 i završava sa zadnjim novčanim tokom u navedenom popisu argumenata. Izračunavanje NPV funkcije temelji se na budućim novčanim tokovima. Ako se vaš prvi novčani tok javlja na početku prvog razdoblja, njegovu vrijednost dodajete rezultatu funkcije NPV, a ne unosite je kao argument funkcije. Za dodatne informacije, pogledajte navedeni primjer.

• Ako je n broj novčanih tokova navedenih u vrijednostima popisa, formula za izračunavanje NPV je:

  

• NPV je slična funkciji PV (sadašnja vrijednost). Osnovna razlika između PV i NPV je u tome što PV dozvoljava da novčani tokovi započinju na kraju ili na početku razdoblja. Za razliku od promjenljivih vrijednosti novčanih tokova kod funkcije NPV, iznosi novčanih tokova kod funkcije PV moraju biti nepromijenjeni za vrijeme investicije. Za informacije o anuitetima i financijskim funkcijama, pogledajte PV.

Primjer 1

U sljedećem primjeru:

• Stopa je godišnja diskontna stopa.

• Vrijednost1 početna je cijena ulaganja za godinu dana.

• Vrijednost2 je povrat iz prve godine.

• Vrijednost3 je povrat iz druge godine.

• Vrijednost4 je povrat iz treće godine.

U ovom primjeru kao jednu od vrijednosti uvrstite početni trošak od 10 000 USD jer se plaćanje odvija na kraju prvog razdoblja.

Primjer 2

U sljedećem primjeru:

• Stopa je godišnja diskontna stopa. To može biti i stopa inflacije ili kamatna stopa konkurentnog ulaganja.

• Vrijednost1 početna je cijena ulaganja za godinu dana.

• Vrijednost2 je povrat iz prve godine.

• Vrijednost3 je povrat iz druge godine.

• Vrijednost4 je povrat iz treće godine.

• Value5 je povrat iz četvrte godine.

• Value6 je povrat iz pete godine.

U primjeru ne uvrstite početni trošak od 40 000 USD kao jednu od vrijednosti jer se plaćanje odvija na početku prvog razdoblja.