Važno: Podrška za Office 2016 i Office 2019 završila je 14. listopada 2025. Nadogradite na Microsoft 365 da biste radili bilo gdje s bilo kojeg uređaja i nastavili primati podršku. Nabavite Microsoft 365
U ovom se članku opisuje korištenje alata za rješavanje, dodatka programa Microsoft Excel koji možete koristiti za analizu "što ako" da biste odredili optimalnu kombinaciju proizvoda.
Kako utvrditi mjesečnu kombinaciju proizvoda koja maksimizira profitabilnost?
Tvrtke često moraju odrediti količinu svakog proizvoda za proizvodnju mjesečno. U najjednostavnijem obliku problem s mješavinom proizvoda uključuje određivanje količine svakog proizvoda koji se treba proizvesti tijekom mjeseca radi maksimiziranja dobiti. Mješavina proizvoda obično se mora pridržavati sljedećih ograničenja:
-
Kombinacija proizvoda ne može koristiti više resursa nego što je dostupno.
-
Postoji ograničena potražnja za svakim proizvodom. Ne možemo proizvesti više proizvoda tijekom mjesec dana od zahtjeva diktat, jer suvišna proizvodnja je uzalud (na primjer, po život po život lijek).
Sada ćemo riješiti sljedeći primjer problema s mješavinom proizvoda. Rješenje tog problema možete pronaći u datoteci Prodmix.xlsx na slici 27-1.
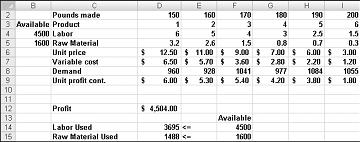
Recimo da radimo za tvrtku koja proizvodi šest različitih proizvoda u njihovoj tvornici. Proizvodnja svakog proizvoda zahtijeva rad i sirovine. Redak 4 na slici 27-1 pokazuje sate rada potrebnih za proizvodnju funte svakog proizvoda, a redak 5 pokazuje kilograme sirovine potrebne za proizvodnju funte svakog proizvoda. Na primjer, za proizvodnju funte proizvoda 1 zahtijeva šest sati rada i 3,2 kilograma sirovina. Za svaki lijek, cijena po funti je dano u retku 6, jedinična cijena po funti je dana u retku 7, a dobit doprinos po funti je dano u retku 9. Na primjer, 2. proizvod prodaje za 11,00 USD po funti, a jedinični trošak iznosi 5,70 USD po funti, a pridonosi dobiti od 5,30 USD po funti. Mjesečna potražnja za svaki lijek je dano u retku 8. Na primjer, potražnja za proizvodom 3 je 1041 funti. Ovaj mjesec, 4500 sati rada i 1600 funti sirovina su dostupni. Kako ova tvrtka može maksimizirati svoju mjesečnu dobit?
Da ne znamo ništa o alatu za rješavanje programa Excel, na ovaj bismo problem napala stvaranjem radnog lista za praćenje dobiti i korištenja resursa povezanih s mješavinom proizvoda. Onda ćemo koristiti probnu i pogrešku za varirati proizvod mix za optimiziranje dobiti bez korištenja više rada ili sirovina nego što je dostupan, i bez proizvodnje bilo kojeg lijeka u višak potražnje. Alat za rješavanje u tom procesu koristimo samo u fazi probne verzije i pogreške. Alat za rješavanje zapravo je modul optimizacije koji besprijekorno izvodi pretraživanje probne verzije i pogreške.
Ključ rješavanja problema s mješavinom proizvoda jest učinkovito izračunavanje korištenja resursa i dobiti povezane s bilo nom mješavinom proizvoda. Važan alat koji možemo koristiti za izračun je funkcija SUMPRODUCT. Funkcija SUMPRODUCT množi odgovarajuće vrijednosti u rasponima ćelija i vraća zbroj tih vrijednosti. Svaki raspon ćelija koji se koristi u SUMPRODUCT procjena mora imati iste dimenzije, što znači da možete koristiti SUMPRODUCT s dva retka ili dva stupca, ali ne i s jednim stupcem i jednim retkom.
Kao primjer kako možemo koristiti funkciju SUMPRODUCT u našem primjeru kombiniranog proizvoda, pokušajmo izračunati korištenje resursa. Naše korištenje radne snage izračunava
(Labor used per pound of drug 1)*(Drug 1 pounds produced)+ (Rad se koristi po funti lijeka 2)*(Lijek 2 funti proizvedeno) + ... (Rad se koristi po funti lijeka 6)*(Lijek 6 funti proizvedeno)
Potrošnju rada mogli bismo na dosadni način izračunati kao D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Isto tako, upotreba sirovina mogla bi se izračunati kao D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. No unos tih formula na radni list za šest proizvoda troši mnogo vremena. Zamislite koliko bi dugo bilo potrebno da radite s tvrtkom koja je proizvela, na primjer, 50 proizvoda u njihovoj biljci. Mnogo jednostavniji način za izračunavanje upotrebe radne snage i sirovina jest kopiranje iz D14 u D15 formulu SUMPRODUCT($D$2:$I$2,D4:I4). Ova formula izračunava D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (što je naša upotreba rada), ali je mnogo lakše ući! Imajte na umu da koristim znak $ s rasponom D2:I2 tako da kada kopiram formulu i dalje snimam kombinaciju proizvoda iz retka 2. Formula u ćeliji D15 izračunava korištenje sirovina.
Na sličan način naša dobit određuje
(Droga 1 dobit po funti)*(Lijek 1 funti proizvedeno) + (Droga 2 dobit po funti)*(Lijek 2 funti proizvedeno) + ... (Droga 6 dobit po funti)*(Lijek 6 funti proizvedeno)
Dobit se jednostavno izračunava u ćeliji D12 pomoću formule SUMPRODUCT(D9:I9;$D$2:$I$2).
Sada možemo prepoznati tri komponente našeg modela alata za rješavanje kombinacija proizvoda.
-
Ciljna ćelija. Naš je cilj maksimizirati dobit (izračunatu u ćeliji D12).
-
Promjena ćelija. Broj funti proizvedenih za svaki proizvod (naveden u rasponu ćelija D2:I2)
-
Ograničenja. Imamo sljedeća ograničenja:
-
Ne koristite više radne snage ili sirovina nego što je dostupno. Odnosno, vrijednosti u ćelijama D14:D15 (korišteni resursi) moraju biti manje ili jednake vrijednostima u ćelijama F14:F15 (dostupni resursi).
-
Nemojte proizvoditi više lijeka nego što je u potražnji. To je, vrijednosti u ćelijama D2:I2 (funti proizvedene od svakog lijeka) moraju biti manje ili jednake potražnji za svaki lijek (navedene u stanicama D8:I8).
-
Ne možemo proizvesti negativnu količinu bilo kojeg lijeka.
-
Prikazat ću vam kako unijeti ciljnu ćeliju, promijeniti ćelije i ograničenja u alat za rješavanje. Zatim samo trebate kliknuti gumb Riješi da biste pronašli kombinaciju proizvoda koji maksimizira dobit!
Da biste započeli, kliknite karticu Podaci, a zatim u grupi Analiza kliknite Alat za rješavanje.
Napomena: Kao što je objašnjeno u poglavlju 26, "Uvod u optimizaciju pomoću alata za rješavanje programa Excel", alat za rješavanje instalira se klikom na gumb Microsoft Office, a zatim mogućnosti programa Excel, a zatim dodaci. Na popisu Upravljanje kliknite Dodaci programa Excel, potvrdite okvir Dodatak alata za rješavanje, a zatim kliknite U redu.
Pojavit će se dijaloški okvir Parametri alata za rješavanje, kao što je prikazano na slici 27-2.
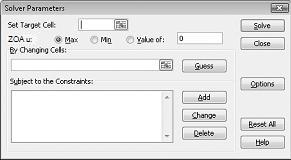
Kliknite okvir Postavi ciljnu ćeliju, a zatim odaberite ćeliju dobit (ćelija D12). Kliknite okvir Promjenom ćelija, a zatim pokažite na raspon D2:I2, koji sadrži kilograme proizvedene od svakog lijeka. Dijaloški okvir sada bi trebao izgledati kao slika 27-3.
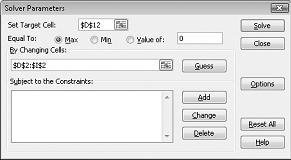
Sada smo spremni dodati ograničenja modelu. Kliknite gumb Dodaj. Prikazat će se dijaloški okvir Dodavanje ograničenja prikazan na slici 27-4.
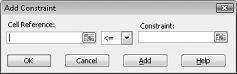
Da biste dodali ograničenja korištenja resursa, kliknite okvir Referenca ćelije, a zatim odaberite raspon D14:D15. Odaberite <= na srednjem popisu. Kliknite okvir Ograničenje, a zatim odaberite raspon ćelija F14:F15. Dijaloški okvir Dodavanje ograničenja sada bi trebao izgledati kao slika 27-5.
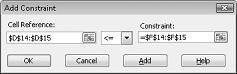
Sada smo osigurali da će se, kada alat za rješavanje pokuša koristiti različite vrijednosti za ćelije koje se mijenjaju, razmotriti samo kombinacije koje zadovoljavaju I D14<=F14 (korišteni rad je manji od ili jednak dostupnom radu) i D15<=F15 (korišteni sirovine su manje od ili jednake dostupnim sirovinama). Kliknite Dodaj da biste unijeli ograničenja potražnje. Ispunite dijaloški okvir Dodavanje ograničenja kao što je prikazano na slici 27-6.
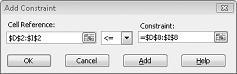
Dodavanjem tih ograničenja osigurava se da će se, kada alat za rješavanje pokuša koristiti različite kombinacije za mijenjanje vrijednosti ćelija, razmotriti samo kombinacije koje zadovoljavaju sljedeće parametre:
-
D2<=D8 (količina proizvedena lijeka 1 je manja od ili jednaka potražnji za lijek 1)
-
E2<=E8 (količina proizvedenog lijeka 2 je manja ili jednaka potražnji za lijek 2)
-
F2<=F8 (količina proizvedena lijeka 3 je manja ili jednaka potražnji za lijek 3)
-
G2<=G8 (količina proizvedena lijeka 4 je manja od ili jednaka potražnji za lijek 4)
-
H2<=H8 (količina proizvedena lijeka 5 je manja od ili jednaka potražnji za lijek 5)
-
I2<=I8 (količina proizvedena lijeka 6 je manja ili jednaka potražnji za lijek 6)
U dijaloškom okviru Dodavanje ograničenja kliknite U redu. Prozor Alata za rješavanje trebao bi izgledati kao slika 27-7.
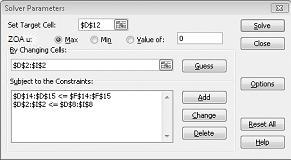
Unesite ograničenje da promjena ćelija mora biti negativna u dijaloškom okviru Mogućnosti alata za rješavanje. Kliknite gumb Mogućnosti u dijaloškom okviru Parametri alata za rješavanje. Potvrdite okvir Pretpostavimo linearni model i okvir Pretpostavi da nije negativan, kao što je prikazano na slici 27-8 na sljedećoj stranici. Kliknite U redu.
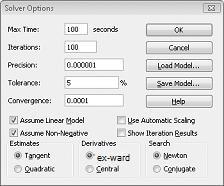
Potvrđivanjem okvira Preuzmi bez negativnog osigurava se da alat za rješavanje uzima u obzir samo kombinacije promjena ćelija u kojima svaka promjena ćelije preuzima vrijednost koja nije negativna. Provjerili smo okvir Pretpostavimo linearni model jer je problem s mješavinom proizvoda posebna vrsta problema alata za rješavanje pod nazivom linearni model. U biti, model alata za rješavanje linearno je u sljedećim uvjetima:
-
Ciljna ćelija izračunava se zbrajanjem uvjeta obrasca (promjenom ćelije)*(konstanta).
-
Svako ograničenje zadovoljava "preduvjet linearnog modela". To znači da se svako ograničenje procjenjuje zbrajanjem uvjeta obrasca (promjenom ćelije )*(konstantom) i usporedbom zbroja s konstantom.
Zašto je taj problem alata za rješavanje linearni? Naša ciljna ćelija (dobit) izračunava se kao
(Droga 1 dobit po funti)*(Lijek 1 funti proizvedeno) + (Droga 2 dobit po funti)*(Lijek 2 funti proizvedeno) + ... (Droga 6 dobit po funti)*(Lijek 6 funti proizvedeno)
Ovo izračunavanje slijedi uzorak u kojem se izvodi vrijednost ciljne ćelije zbrajanjem uvjeta obrasca (promjenom ćelije)*(konstanta).
Naše ograničenje rada se vrednuju usporedbom vrijednosti izvedene iz (Rad se koristi po funti lijeka 1)*(Lijek 1 funti proizveden) + (Rad se koristi po funti lijeka 2)*(Lijek 2 funti proizvedeno)+ ... (Rad nased po funti droge 6)*(Lijek 6 funti proizvedeno) na rad dostupan.
Stoga se ograničenje rada vrednuju zbrajanjem uvjeta obrasca (promjenom ćelije )*(konstantom) i usporedbom zbroja s konstantom. Ograničenje rada i ograničenje sirovina zadovoljavaju linearni model.
Naša ograničenja potražnje u obliku
(Lijek 1 proizveden)<=(Lijek 1 Potražnja) (Lijek 2 proizveden)<=(Lijek 2 Potražnja) §(Lijek 6 proizveden)<=(Lijek 6 Potražnja)
Svako ograničenje potražnje zadovoljava i zahtjev linearnog modela jer se svaki izračunava zbrajanjem uvjeta obrasca (promjenom ćelije)*(konstantom) i usporedbom zbroja s konstantom.
Nakon što je pokazala da je naš model mješavine proizvoda linearni model, zašto bi nas bilo briga?
-
Ako je model alata za rješavanje linearni i odabrali smo Pretpostavi linearni model, alat za rješavanje zagarantiran je da će pronaći optimalno rješenje za model alata za rješavanje. Ako model alata za rješavanje nije linearno, alat za rješavanje može ili ne može pronaći optimalno rješenje.
-
Ako je model alata za rješavanje linearni, a mi odaberete Pretpostavi linearni model, alat za rješavanje koristi vrlo učinkovit algoritam (simplex metoda) da bi se pronašlo optimalno rješenje modela. Ako je model alata za rješavanje linearni, a ne odabrali pretpostavimo linearni model, alat za rješavanje koristi vrlo neučinkovit algoritam (metodu GRG2) i može imati poteškoća s pronalaženjem optimalnog rješenja modela.
Kada u dijaloškom okviru Mogućnosti alata za rješavanje kliknete U redu, vratit ćemo se na glavni dijaloški okvir Alat za rješavanje, prikazan ranije na slici 27-7. Kada kliknemo Riješi, alat za rješavanje izračunava optimalno rješenje (ako postoji) za naš model kombiniranog proizvoda. Kao što sam rekao u poglavlju 26, optimalno rješenje za proizvod mix modela će biti skup promjena vrijednosti ćelija (funti proizvedenih od svakog lijeka) koji maksimizira dobit preko skupa svih izvedivih rješenja. Opet, izvedivo rješenje skup je promjena vrijednosti ćelija koje zadovoljavaju sva ograničenja. Promjenom vrijednosti ćelija prikazanih na slici 27-9 moguće je rješenje jer sve razine proizvodnje nisu negativne, proizvodne razine ne premašuju potražnju, a korištenje resursa ne premašuje dostupne resurse.
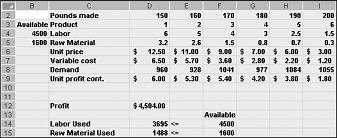
Promjene vrijednosti ćelija prikazane na slici 27-10 na sljedećoj stranici predstavljaju neuočljivo rješenje iz sljedećih razloga:
-
Mi proizvodimo više droge 5 od potražnje za njega.
-
Koristimo više rada nego što je dostupno.
-
Koristimo više sirovina nego što je dostupno.
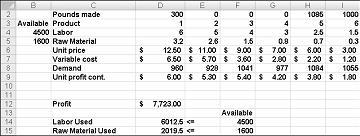
Kada kliknete Riješi, alat za rješavanje brzo pronalazi optimalno rješenje prikazano na slici 27-11. Da biste zadržali optimalne vrijednosti rješenja na radnom listu, morate odabrati Zadrži rješenje alata za rješavanje.
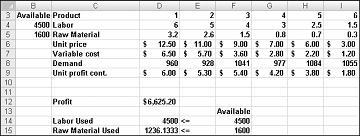
Naša droga tvrtka može maksimizirati svoju mjesečnu dobit na razini od $6,625.20 proizvodnju 596.67 funti droge 4, 1084 funti droge 5, i ništa od drugih lijekova! Ne možemo odrediti možemo li ostvariti maksimalnu dobit od 6625,20 USD na druge načine. Sve u što možemo biti sigurni je da s našim ograničenim resursima i potražnjom, ne postoji način da se više od 6.627,20 dolara ovaj mjesec.
Pretpostavimo da je potrebno zadirati tu potražnju za svakim proizvodom. (Pogledajte radni list Bez mogućeg rješenja u datoteci Prodmix.xlsx.) Nakon toga moramo promijeniti ograničenja potražnje iz D2:I2<=D8:I8 u D2:I2>=D8:I8. Da biste to učinili, otvorite alat za rješavanje, odaberite ograničenje D2:I2<=D8:I8, a zatim kliknite Promijeni. Pojavit će se dijaloški okvir Promjena ograničenja prikazan na slici 27- 12.
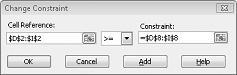
Odaberite >=, a zatim kliknite U redu. Sada smo osigurali da alat za rješavanje razmotri promjenu samo vrijednosti ćelija koje zadovoljavaju sve zahtjeve. Kada kliknete Riješi, prikazat će se poruka "Alat za rješavanje nije mogao pronaći izvedivo rješenje". Ova poruka ne znači da smo pogriješili u modelu, već da s ograničenim resursima ne možemo zadovoljiti zahtjeve za svim proizvodima. Rješavač nam jednostavno govori da ako želimo zadovoljiti potražnju za svakim proizvodom, moramo dodati više rada, više sirovina ili više od oboje.
Pogledajmo što će se dogoditi ako dozvolimo neograničenu potražnju za svaki proizvod i dopustili smo da se negativne količine proizvode od svakog lijeka. (Taj problem alata za rješavanje možete vidjeti na radnom listu Postavljanje vrijednosti ne konvergira u datoteci Prodmix.xlsx.) Da biste pronašli optimalno rješenje za tu situaciju, otvorite Alat za rješavanje, kliknite gumb Mogućnosti i poništite okvir Pretpostavi da nije negativno. U dijaloškom okviru Parametri alata za rješavanje odaberite ograničenje potražnje D2:I2<=D8:I8, a zatim kliknite Izbriši da biste uklonili ograničenje. Kada kliknete Riješi, alat za rješavanje vraća poruku "Postavljanje vrijednosti ćelija ne konvergira". Ova poruka znači da ako je ciljna ćelija maksimizirana (kao u našem primjeru), postoje moguća rješenja s proizvoljno velikim vrijednostima ciljnih ćelija. (Ako je ciljna ćelija minimizirana, poruka "Postavljanje vrijednosti ćelija Ne konvergira" znači da postoje moguća rješenja s proizvoljno malim vrijednostima ciljnih ćelija.) U našoj situaciji, dopuštajući negativnu proizvodnju lijeka, na snazi smo "stvoriti" resurse koji se mogu koristiti za proizvoljno velike količine drugih lijekova. S obzirom na neograničenu potražnju, to nam omogućuje da zaradimo neograničen profit. U stvarnoj situaciji ne možemo zaraditi neograničenu količinu novca. Ukratko, ako vidite "Set Values Do Not Converge", vaš model ima pogrešku.
-
Pretpostavimo da naša tvrtka za drogu može kupiti do 500 sati rada za $1 više po satu od trenutnih troškova rada. Kako maksimizirati dobit?
-
U postrojenju za proizvodnju čipova četiri tehničara (A, B, C i D) proizvode tri proizvoda (proizvodi 1, 2 i 3). Ovaj mjesec proizvođač čipa može prodati 80 jedinica proizvoda 1, 50 jedinica proizvoda 2 i najviše 50 jedinica proizvoda 3. Tehničar A može izraditi samo proizvode 1 i 3. Tehničar B može izraditi samo proizvode 1 i 2. Tehničar C može izraditi samo proizvod 3. Tehničar D može izraditi samo proizvod 2. Za svaku proizvedenu jedinicu proizvodi doprinose sljedećoj dobiti: Proizvod 1, 6 $; Proizvod 2, $7; i proizvod 3, 10 USD. Vrijeme (u satima) potrebno svakom tehničaru za proizvodnju proizvoda je kako slijedi:
Proizvod
Tehničar A
Tehničar B
Tehničar C
Tehničar D
1
2
2,5
Nije moguće učiniti
Nije moguće učiniti
2
Nije moguće učiniti
3
Nije moguće učiniti
3,5
3
3
Nije moguće učiniti
4
Nije moguće učiniti
-
Svaki tehničar može raditi do 120 sati mjesečno. Kako proizvođač čipa može maksimizirati svoju mjesečnu dobit? Pretpostavimo da je moguće stvoriti decimalni broj jedinica.
-
Postrojenje za proizvodnju računala proizvodi miševe, tipkovnice i igraće igraće palice. Dobit po jedinici, potrošnja rada po jedinici, mjesečna potražnja i potrošnja strojnog vremena po jedinici navedene su u sljedećoj tablici:
Miševi
Tipkovnice
Joystick
Dobit/jedinica
8 KN (100 kn)
11 KN (11 KN)
9 USD (100 kn)
Korištenje rada/jedinica
0,2 sata
0,3 sata
0,24 sata
Vrijeme/jedinica stroja
0,04 sat
0,055 sat
0,04 sat
Mjesečna potražnja
15 000
27,000
11,000
-
Svakog mjeseca dostupno je ukupno 13.000 radnih sati i 3000 sati strojnog vremena. Kako proizvođač može maksimizirati svoj mjesečni doprinos dobiti od biljke?
-
Riješiti naš lijek primjer pod pretpostavkom da je minimalna potražnja od 200 jedinica za svaki lijek mora biti ispunjen.
-
Jason pravi dijamantne narukvice, ogrlice i nauљnice. Želi raditi maksimalno 160 sati mjesečno. Ima 800 unca rombova. Dobit, vrijeme rada i uncama dijamanta potrebnih za proizvodnju svakog proizvoda navedene su u nastavku. Ako je potražnja za svaki proizvod neograničena, kako Jason može maksimizirati svoju dobit?
Proizvod
Jedinična dobit
Radno vrijeme po jedinici
Unca rombova po jedinici
Narukvica
1500,00 kn
.35
1,2
Ogrlica
1000 kn
.15
.75
Naušnice
500 kn
0,05
.5










