Egy statisztikai sokaság várható értékének normális eloszlás használatával számított megbízhatósági intervallumát adja vissza.
Leírás
A megbízhatósági intervallum értékek tartománya. A minta középértéke (x) ennek a tartománynak a középpontjában van, a tartomány pedig x ± CONFIDENCE.NORM. Ha például x a levélben megrendelt termékek kézbesítési idejének középértékét jelenti, x ± MEGBÍZHATÓSÁG. A NORM egy sokasági középtartomány. A statisztikai sokaság minden μ0 várható értékére vonatkoztatva a tartományon belül, annak valószínűsége, hogy a középérték távolabb lesz μ0-tól mint x, nagyobb, mint alfa; a statisztikai sokaság minden μ0 várható értékére vonatkoztatva a tartományon kívül, annak valószínűsége, hogy a középérték távolabb lesz μ0-tól mint x, kevesebb, mint alfa. Vagyis tegyük fel, hogy az x, a szórás és a méret segítségével létrehoz alfa pontossági szinten egy kétszélű próbát annak a hipotézisnek az ellenőrzésére, hogy a statisztikai sokaság várható értéke μ0. Nem veti el a hipotézist, ha μ0 a megbízhatósági tartományon belül található, de elveti a hipotézist, ha μ0 a megbízhatósági tartományon kívül esik. A megbízhatósági intervallumból azonban nem következik, hogy a következő csomag szállítási ideje 1-alfa valószínűséggel a megbízhatósági intervallumon belül lesz.
Szintaxis
MEGBÍZHATÓSÁG.NORM(alfa,szórás,méret)
A MEGBÍZHATÓSÁG.NORM függvény szintaxisa az alábbi argumentumokat foglalja magában:
-
Alfa: Megadása kötelező. A megbízhatósági szint kiszámításához használt pontossági szint. A megbízhatósági szint egyenlő 100*(1-alfa), vagyis a 0,05 alfaérték 95%-os megbízhatósági szintet takar.
-
Szórás: Megadása kötelező. Az adattartomány sokasági szórása, és feltételezzük, hogy ismert.
-
Méret Megadása kötelező. A mintanagyság.
Megjegyzések
-
Ha bármely argumentum nem számérték, a MEGBÍZHATÓSÁG.NORM függvény az #ÉRTÉK! hibaértéket adja eredményül.
-
Amennyiben alfa ≤ 0 vagy alfa ≥ 1, a MEGBÍZHATÓSÁG.NORM függvény a #SZÁM! hibaértéket adja vissza.
-
Ha a szórás ≤ 0, a MEGBÍZHATÓSÁG.NORM függvény a #SZÁM! hibaértéket adja eredményül.
-
Amennyiben a méret nem egész szám, egésszé lesz csonkítva.
-
Ha a méret < 1, a MEGBÍZHATÓSÁG.NORM függvény a #SZÁM! hibaértéket adja eredményül.
-
Ha feltételezi, hogy az alfa értéke 0,05, akkor a normális (eloszlás)görbe alatti területtel (1- alfa) kell számolnia (95%). Ez az érték ± 1,96. A megbízhatósági intervallum ebből adódóan:
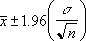
Példa
Másolja a mintaadatokat az alábbi táblázatból, és illessze be őket egy új Excel-munkalap A1 cellájába. Ha azt szeretné, hogy a képletek megjelenítsék az eredményt, jelölje ki őket, és nyomja le az F2, majd az Enter billentyűt. Szükség esetén módosíthatja az oszlopok szélességét, hogy az összes adat látható legyen.
|
Adatok |
Leírás |
|
|
0,05 |
Megbízhatósági szint |
|
|
2,5 |
Sokaság adattartományon vett szórása |
|
|
50 |
A minta mérete |
|
|
Képlet |
Leírás |
Eredmény |
|
=MEGBÍZHATÓSÁG.NORM(A2;A3;A4) |
Statisztikai sokaság megbízhatósági intervalluma. Más szóval a statisztikai sokaság munkába érési időre vonatkozó várható értékének megbízhatósági intervalluma egyenlő 30 ± 0,692952 perccel vagy a 29,3 és 30,7 perc közötti tartománnyal. |
0,692952 |










