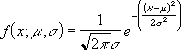A függvény megadott várható értéknél és szórásnál a normális eloszlásfüggvényt számítja ki. A függvény felhasználása a statisztikában széles körű, beleértve a hipotézis-vizsgálatot.
Szintaxis
NORM.ELOSZLÁS(x;középérték;szórás,eloszlásfv)
A NORM.ELOSZLÁS függvény szintaxisa az alábbi argumentumokat foglalja magában:
-
X: Megadása kötelező. Az az érték, amelynél az eloszlást ki kell számítani.
-
Középérték: Megadása kötelező. Az eloszlás középértéke (várható értéke).
-
Szórás: Megadása kötelező. Az eloszlás szórása.
-
Eloszlásfv: Megadása kötelező. Logikai érték, amely a függvény fajtáját határozza meg. Ha az eloszlás értéke IGAZ, akkor a NORM. A ELOSZLÁS az eloszlásfüggvényt adja vissza; ha HAMIS, akkor a sűrűségfüggvényt adja vissza.
Megjegyzések
-
Ha a középérték vagy a szórás argumentum értéke nem szám, akkor a NORM.ELOSZLÁS az #ÉRTÉK! hibaértéket adja eredményül.
-
Ha szórás ≤ 0, akkor a NORM.ELOSZLÁS eredménye a #SZÁM! hibaérték lesz.
-
Ha középérték = 0, szórás = 1 és eloszlásfv = IGAZ, akkor a NORM.ELOSZLÁS a standard normális eloszlást (NORM.S.ELOSZLÁS) adja meg.
-
A normális sűrűségfüggvény (eloszlásfv = HAMIS) kiszámítása az alábbi képlet alapján történik:
-
Ha eloszlásfv = IGAZ, a képlet a negatív végtelentől a megadott képlet x értékéig vett integrált adja.
Példa
Másolja a mintaadatokat az alábbi táblázatból, és illessze be őket egy új Excel-munkalap A1 cellájába. Ha azt szeretné, hogy a képletek megjelenítsék az eredményt, jelölje ki őket, és nyomja le az F2, majd az Enter billentyűt. Szükség esetén módosíthatja az oszlopok szélességét, hogy az összes adat látható legyen.
|
Adatok |
Leírás |
|
|
42 |
Az az érték, amelyre az eloszlást ki szeretné számítani |
|
|
40 |
Az eloszlás középértéke |
|
|
1,5 |
Az eloszlás szórása |
|
|
Képlet |
Leírás |
Eredmény |
|
=NORM.ELOSZLÁS(A2;A3;A4;IGAZ) |
Az eloszlásfüggvény eredménye a fenti adatokra |
0,9087888 |
|
=NORM.ELOSZLÁS(A2;A3;A4;HAMIS) |
A sűrűségfüggvény eredménye a fenti adatokra |
0,10934 |