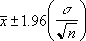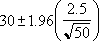Mengembalikan interval kepercayaan untuk rata-rata populasi dengan distribusi normal. Interval kepercayaan adalah rentang di salah satu sisi rata-rata sampel. Misalnya, jika Anda memesan produk melalui email, Anda bisa menentukan, dengan tingkat kepercayaan tertentu, produk paling awal dan terbaru akan tiba.
Sintaks
CONFIDENCE(alpha,standard_dev,size)
Alfa adalah tingkat signifikansi yang digunakan untuk menghitung tingkat kepercayaan. Tingkat kepercayaan sama dengan 100*(1 - alpha)%, atau dengan kata lain, alpha dari 0,05 menunjukkan tingkat kepercayaan 95 persen.
Standard_dev adalah simpangan baku populasi untuk rentang data dan diasumsikan diketahui.
Ukuran adalah ukuran sampel.
Keterangan
-
Jika ada argumen yang nonnumerik, CONFIDENCE mengembalikan #VALUE! nilai kesalahan.
-
Jika alpha ≤ 0 atau alpha ≥ 1, CONFIDENCE mengembalikan #NUM! nilai kesalahan.
-
Jika standard_dev ≤ 0, CONFIDENCE mengembalikan #NUM! nilai kesalahan.
-
Jika size bukan bilangan bulat, maka dipotong.
-
Jika ukuran < 1, CONFIDENCE mengembalikan #NUM! nilai kesalahan.
-
Jika diasumsikan alpha sama dengan 0,05, kita perlu menghitung area pada kurva normal standar yang sama dengan (1 - alpha), atau 95 persen. Nilai ini ± 1,96. Oleh karena itu, interval kepercayaannya:
Contoh
Misalkan kita mengamati bahwa, dalam sampel 50 komuter kita, rata-rata lama perjalanan ke tempat kerja adalah 30 menit dengan simpangan baku populasi 2,5. Kita dapat 95 persen yakin bahwa rata-rata populasi berada dalam interval:
|
Alfa |
StdDev |
Ukuran |
Rumus |
Deskripsi (Hasil) |
|---|---|---|---|---|
|
0,05 |
.5 |
50 |
=CONFIDENCE([Alpha],[StdDev],[Size]) |
Interval kepercayaan untuk rata-rata populasi. Dengan kata lain, panjang rata-rata perjalanan ke tempat kerja sama dengan 30 ± 0,692951 menit, atau 29,3 hingga 30,7 menit. (0.692951) |