Menggunakan Solver untuk menentukan campuran produk yang optimal

Bagaimana cara menentukan campuran produk bulanan yang memaksimalkan profitabilitas?

Perusahaan seringkali perlu menentukan kuantitas setiap produk untuk diproduksi setiap bulan. Dalam bentuk yang paling sederhana, masalah campuran produk melibatkan cara menentukan jumlah setiap produk yang harus diproduksi selama satu bulan untuk memaksimalkan keuntungan. Campuran produk biasanya harus mematuhi batasan berikut:

• Campuran produk tidak dapat menggunakan lebih banyak sumber daya daripada yang tersedia.

• Ada permintaan terbatas untuk setiap produk. Kami tidak dapat memproduksi lebih banyak produk selama sebulan daripada pendiktean permintaan, karena kelebihan produksi terbuang (misalnya, obat yang mudah mati).

Mari kita selesaikan contoh masalah campuran produk berikut ini. Anda dapat menemukan solusi untuk masalah ini dalam Prodmix.xlsx file, yang diperlihatkan dalam Gambar 27-1.

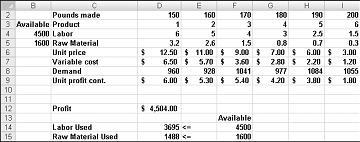
Katakanlah kita bekerja untuk perusahaan obat yang memproduksi enam produk berbeda di pabrik mereka. Produksi setiap produk memerlukan tenaga kerja dan bahan baku. Baris 4 dalam Gambar 27-1 menunjukkan jam kerja yang diperlukan untuk menghasilkan satu pon dari setiap produk, dan baris 5 menunjukkan pon bahan baku yang diperlukan untuk menghasilkan satu pon dari setiap produk. Misalnya, memproduksi pon Produk 1 memerlukan enam jam tenaga kerja dan 3,2 pon bahan baku. Untuk setiap obat, harga per pound diberikan dalam baris 6, biaya satuan per pound diberikan dalam baris 7, dan kontribusi laba per pound diberikan dalam baris 9. Misalnya, Produk 2 dijual seharga $11,00 per pound, menimbulkan biaya satuan sebesar $5,70 per pound, dan menyumbang laba $5,30 per pound. Permintaan bulan untuk setiap obat diberikan di baris 8. Misalnya, permintaan untuk Produk 3 adalah 1041 pound. Bulan ini, 4500 jam tenaga kerja dan 1600 pound bahan baku tersedia. Bagaimana perusahaan ini dapat memaksimalkan laba bulanannya?

Jika kami tidak tahu apa-apa tentang Solver Excel, kami akan menyerang masalah ini dengan membuat lembar kerja untuk melacak penggunaan laba dan sumber daya yang terkait dengan campuran produk. Kemudian kami akan menggunakan uji coba dan kesalahan untuk memvariasikan campuran produk untuk mengoptimalkan laba tanpa menggunakan lebih banyak tenaga kerja atau bahan baku daripada yang tersedia, dan tanpa memproduksi obat apa pun yang melebihi permintaan. Kami menggunakan Solver dalam proses ini hanya pada tahap uji coba dan kesalahan. Pada dasarnya, Solver adalah mesin optimisasi yang dengan sempurna melakukan pencarian uji coba dan kesalahan.

Kunci untuk memecahkan masalah campuran produk adalah menghitung penggunaan sumber daya dan laba yang terkait dengan campuran produk tertentu secara efisien. Alat penting yang dapat kita gunakan untuk membuat komputasi ini adalah fungsi SUMPRODUCT. Fungsi SUMPRODUCT mengalikan nilai terkait dalam rentang sel dan mengembalikan jumlah nilai tersebut. Setiap rentang sel yang digunakan dalam evaluasi SUMPRODUCT harus memiliki dimensi yang sama, yang menyiratkan bahwa Anda bisa menggunakan SUMPRODUCT dengan dua baris atau dua kolom, tetapi tidak dengan satu kolom dan satu baris.

Sebagai contoh bagaimana kita dapat menggunakan fungsi SUMPRODUCT dalam contoh campuran produk kita, mari kita coba menghitung penggunaan sumber daya kita. Penggunaan tenaga kerja kami dihitung dengan

(Tenaga kerja yang digunakan per pon obat 1)*(Obat 1 pon diproduksi)+
(Tenaga kerja yang digunakan per pon obat 2)*(Obat 2 pon diproduksi) + ...
(Tenaga kerja yang digunakan per pon obat 6)*(Obat 6 pon diproduksi)

Kami dapat menghitung penggunaan tenaga kerja dengan cara yang lebih melelahkan sebagai D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Demikian pula, penggunaan bahan baku dapat dihitung sebagai D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Namun, memasukkan rumus ini dalam lembar kerja untuk enam produk memakan waktu. Bayangkan berapa lama waktu yang diperlukan jika Anda bekerja dengan perusahaan yang memproduksi, misalnya, 50 produk di pabrik mereka. Cara yang jauh lebih mudah untuk menghitung penggunaan tenaga kerja dan bahan baku adalah dengan menyalin dari D14 ke D15 rumus SUMPRODUCT($D$2:$I$2,D4:I4). Rumus ini menghitung D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (yang merupakan penggunaan tenaga kerja kami) tetapi jauh lebih mudah untuk dimasukkan! Perhatikan bahwa saya menggunakan tanda $ dengan rentang D2:I2 sehingga ketika saya menyalin rumus, saya masih mengambil campuran produk dari baris 2. Rumus dalam sel D15 menghitung penggunaan bahan baku.

Dengan cara yang sama, keuntungan kita ditentukan oleh

(Obat 1 profit per pound)*(Obat 1 pon diproduksi) +
(Obat 2 profit per pound)*(Obat 2 pon diproduksi) + ...
(Obat 6 laba per pon)*(Obat 6 pound diproduksi)

Profit mudah dihitung di sel D12 dengan rumus SUMPRODUCT(D9:I9,$D$2:$I$2).

Kami sekarang dapat mengidentifikasi tiga komponen model Solver campuran produk kami.

• Sel target. Tujuan kami adalah untuk memaksimalkan laba (dihitung dalam sel D12).

• Mengubah sel. Jumlah pound yang dihasilkan dari setiap produk (tercantum dalam rentang sel D2:I2)

• Kendala. Kami memiliki batasan berikut:

  • Jangan gunakan lebih banyak tenaga kerja atau bahan baku daripada yang tersedia. Artinya, nilai dalam sel D14:D15 (sumber daya yang digunakan) harus kurang dari atau sama dengan nilai dalam sel F14:F15 (sumber daya yang tersedia).

  • Jangan memproduksi lebih dari obat daripada yang diminati. Artinya, nilai dalam sel D2:I2 (pound yang dihasilkan dari setiap obat) harus kurang dari atau sama dengan permintaan untuk setiap obat (tercantum dalam sel D8:I8).

  • Kita tidak bisa menghasilkan jumlah negatif dari obat apa pun.

Saya akan menunjukkan cara memasukkan sel target, mengubah sel, dan batasan menjadi Solver. Kemudian yang perlu Anda lakukan adalah mengklik tombol Atasi untuk menemukan campuran produk yang memaksimalkan laba!

Untuk memulai, klik tab Data, dan dalam grup Analisis, klik Solver.

Kotak dialog Parameter Solver akan muncul, seperti yang diperlihatkan dalam Gambar 27-2.

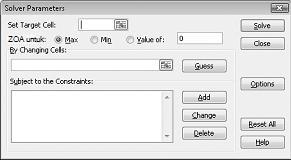
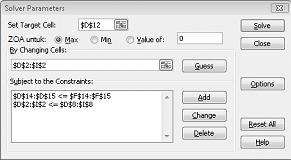
Klik kotak Atur Sel Target lalu pilih sel laba kami (sel D12). Klik kotak Dengan Mengubah Sel lalu arahkan ke rentang D2:I2, yang berisi pound yang dihasilkan dari setiap obat. Kotak dialog sekarang akan terlihat Gambar 27-3.

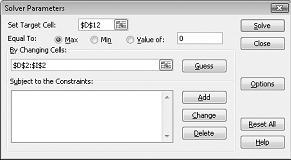
Kami kini siap menambahkan batasan ke model. Klik tombol Tambahkan. Anda akan melihat kotak dialog Tambahkan Batasan, yang diperlihatkan dalam Gambar 27-4.

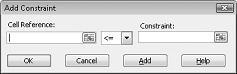
Untuk menambahkan batasan penggunaan sumber daya, klik kotak Referensi Sel, lalu pilih rentang D14:D15. Pilih <= dari daftar tengah. Klik kotak Batasan, lalu pilih rentang sel F14:F15. Kotak dialog Tambahkan Batasan sekarang akan terlihat seperti Gambar 27-5.

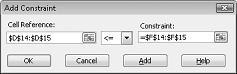
Kami telah memastikan bahwa saat Solver mencoba nilai yang berbeda untuk sel yang berubah, hanya kombinasi yang memenuhi D14<=F14 (tenaga kerja yang digunakan kurang dari atau sama dengan tenaga kerja yang tersedia) dan D15<=F15 (bahan baku yang digunakan kurang dari atau sama dengan bahan baku yang tersedia) akan dipertimbangkan. Klik Tambahkan untuk memasukkan batasan permintaan. Isi kotak dialog Tambahkan Batasan seperti yang diperlihatkan dalam Gambar 27-6.

Menambahkan batasan ini memastikan bahwa ketika Solver mencoba kombinasi yang berbeda untuk nilai sel yang berubah, hanya kombinasi yang memenuhi parameter berikut ini yang akan dipertimbangkan:

• D2<=D8 (jumlah yang dihasilkan dari Obat 1 kurang dari atau sama dengan permintaan Obat 1)

• E2<=E8 (jumlah produksi Obat 2 kurang dari atau sama dengan permintaan Obat 2)

• F2<=F8 (jumlah yang dihasilkan dari Obat 3 dibuat kurang dari atau sama dengan permintaan obat 3)

• G2<=G8 (jumlah yang dihasilkan dari Obat 4 yang dibuat kurang dari atau sama dengan permintaan obat 4)

• H2<=H8 (jumlah yang dihasilkan dari Obat 5 dibuat kurang dari atau sama dengan permintaan Obat 5)

• I2<=I8 (jumlah yang dihasilkan dari Obat 6 dibuat kurang dari atau sama dengan permintaan obat 6)

Klik OK dalam kotak dialog Tambahkan Batasan. Jendela Solver akan terlihat seperti Gambar 27-7.

Kami memasukkan batasan bahwa mengubah sel harus non-negatif dalam kotak dialog Opsi Solver. Klik tombol Opsi dalam kotak dialog Parameter Solver. Centang kotak Asumsikan Model Linear dan kotak Asumsikan Non-Negatif, seperti yang diperlihatkan dalam Gambar 27-8 di halaman berikutnya. Klik OK.

Mencentang kotak Asumsikan Non-Negatif memastikan bahwa Solver hanya mempertimbangkan kombinasi mengubah sel di mana setiap sel yang berubah mengasumsikan nilai non-negatif. Kami mencentang kotak Asumsikan Model Linear karena masalah campuran produk adalah tipe khusus masalah Solver yang disebut model linear. Pada dasarnya, model Solver linear di bawah kondisi berikut:

• Sel target dihitung dengan menambahkan ketentuan formulir (mengubah sel)*(konstanta).

• Setiap batasan memenuhi "persyaratan model linear." Ini berarti bahwa setiap batasan dievaluasi dengan menambahkan ketentuan formulir (mengubah sel)*(konstanta) dan membandingkan jumlah dengan konstanta.

Mengapa Solver ini bermasalah linear? Sel target (laba) kami dihitung sebagai

(Obat 1 profit per pound)*(Obat 1 pon diproduksi) +
(Obat 2 profit per pound)*(Obat 2 pon diproduksi) + ...
(Obat 6 laba per pon)*(Obat 6 pound diproduksi)

Komputasi ini mengikuti pola di mana nilai sel target berasal dengan menambahkan istilah formulir secara bersamaan (mengubah sel)*(konstanta).

Kendala tenaga kerja kami dievaluasi dengan membandingkan nilai yang berasal dari (Tenaga Kerja yang digunakan per pon Obat 1)*(Obat 1 pon diproduksi) + (Tenaga kerja digunakan per pon Obat 2)*(Obat 2 pon diproduksi)+ ... (Pekerjakan kamied per pon Obat 6)*(Obat 6 pon diproduksi) untuk tenaga kerja yang tersedia.

Oleh karena itu, batasan tenaga kerja dievaluasi dengan menambahkan ketentuan formulir (mengubah sel)*(konstanta) dan membandingkan jumlah dengan konstanta. Baik batasan tenaga kerja maupun batasan bahan baku memenuhi persyaratan model linear.

Batasan permintaan kami mengambil formulir

(Obat 1 diproduksi)<=(Obat 1 Permintaan)
(Obat 2 diproduksi)<=(Obat 2 Permintaan)

§(Obat 6 diproduksi)<=(Obat 6 Permintaan)

Setiap batasan permintaan juga memenuhi persyaratan model linear, karena masing-masing dievaluasi dengan menambahkan ketentuan formulir (mengubah sel)*(konstanta) dan membandingkan jumlah dengan konstanta.

Setelah menunjukkan bahwa model campuran produk kami adalah model linear, mengapa kita harus peduli?

• Jika model Solver linear dan kami memilih Asumsikan Model Linear, Solver dijamin akan menemukan solusi optimal untuk model Solver. Jika model Solver tidak linear, Solver mungkin atau mungkin tidak menemukan solusi optimal.

• Jika model Solver linear dan kami memilih Asumsikan Model Linear, Solver menggunakan algoritma yang sangat efisien (metode simpleks) untuk menemukan solusi optimal model. Jika model Solver linear dan kami tidak memilih Asumsikan Model Linear, Solver menggunakan algoritma yang sangat tidak efisien (metode GRG2) dan mungkin mengalami kesulitan menemukan solusi optimal model.

Setelah mengklik OK dalam kotak dialog Opsi Solver, kami kembali ke kotak dialog Solver utama, yang diperlihatkan sebelumnya dalam Gambar 27-7. Ketika kami mengklik Solve, Solver menghitung solusi optimal (jika ada) untuk model campuran produk kami. Seperti yang saya nyatakan dalam Bab 26, solusi optimal untuk model campuran produk adalah sekumpulan nilai sel yang berubah (pound yang dihasilkan dari setiap obat) yang memaksimalkan laba atas serangkaian solusi yang layak. Sekali lagi, solusi yang layak adalah sekumpulan mengubah nilai sel yang memenuhi semua batasan. Mengubah nilai sel yang diperlihatkan dalam Gambar 27-9 adalah solusi yang layak karena semua tingkat produksi tidak negatif, tingkat produksi tidak melebihi permintaan, dan penggunaan sumber daya tidak melebihi sumber daya yang tersedia.

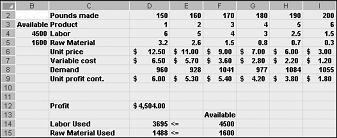
Nilai sel yang berubah diperlihatkan dalam Gambar 27-10 di halaman berikutnya menunjukkan solusi yang tidak mungkin karena alasan berikut:

• Kami memproduksi lebih banyak Obat 5 daripada permintaan untuk itu.

• Kami menggunakan lebih banyak tenaga kerja daripada yang tersedia.

• Kami menggunakan lebih banyak bahan baku daripada yang tersedia.

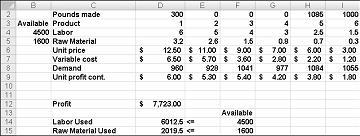
Setelah mengklik Solve, Solver dengan cepat menemukan solusi optimal yang diperlihatkan dalam Gambar 27-11. Anda perlu memilih Pertahankan Solusi Solver untuk mempertahankan nilai solusi optimal dalam lembar kerja.

Perusahaan obat kami dapat memaksimalkan laba bulanannya pada tingkat $ 6.625,20 dengan menghasilkan 596,67 pon Obat 4, 1084 pon Obat 5, dan tidak ada obat lain! Kami tidak dapat menentukan apakah kami dapat mencapai laba maksimum $6.625,20 dengan cara lain. Yang dapat kami pastikan adalah bahwa dengan sumber daya dan permintaan kami yang terbatas, tidak ada cara untuk membuat lebih dari $ 6,627.20 bulan ini.