Artikel ini diadaptasi dari Analisis Data dan Pemodelan Bisnis Microsoft Excel oleh Wayne L. Winston.
-
Siapa yang menggunakan simulasi Monte Carlo?
-
Apa yang terjadi ketika Anda mengetik =RAND() dalam sel?
-
Bagaimana Anda bisa mensimulasikan nilai variabel acak diskrit?
-
Bagaimana Anda bisa mensimulasikan nilai dari variabel acak normal?
-
Bagaimana perusahaan kartu ucapan dapat menentukan berapa banyak kartu yang akan dihasilkan?
Kami ingin memperkirakan probabilitas kejadian yang tidak pasti secara akurat. Misalnya, apa probabilitas bahwa arus kas produk baru akan memiliki nilai bersih bersih saat ini (NPV) yang positif? Apa faktor risiko portofolio investasi kami? Simulasi Monte Carlo memungkinkan kita untuk membuat model situasi yang menghadirkan ketidakpastian dan kemudian memainkannya di komputer ribuan kali.
Catatan: Nama Simulasi Monte Carlo berasal dari simulasi komputer yang dilakukan selama 1930-an dan 1940-an untuk memperkirakan probabilitas bahwa reaksi berantai yang diperlukan agar bom atom meledak akan berhasil. Fisikawan yang terlibat dalam pekerjaan ini adalah penggemar berat perjudian, sehingga mereka memberikan simulasi nama kode Monte Carlo.
Dalam lima bab berikutnya, Anda akan melihat contoh cara menggunakan Excel untuk melakukan simulasi Monte Carlo.
Banyak perusahaan menggunakan simulasi Monte Carlo sebagai bagian penting dari proses pengambilan keputusan mereka. Berikut beberapa contohnya.
-
General Motors, Proctor dan Gamble, Pfizer, Bristol-Myers Squibb, dan Eli Lilly menggunakan simulasi untuk memperkirakan pengembalian rata-rata dan faktor risiko produk baru. Di GM, informasi ini digunakan oleh CEO untuk menentukan produk mana yang datang ke pasar.
-
GM menggunakan simulasi untuk kegiatan seperti memperkirakan pendapatan bersih untuk korporasi, memprediksi biaya struktural dan pembelian, dan menentukan kerentanannya terhadap berbagai jenis risiko (seperti perubahan suku bunga dan fluktuasi nilai tukar).
-
Lilly menggunakan simulasi untuk menentukan kapasitas tanaman yang optimal untuk setiap obat.
-
Proctor dan Gamble menggunakan simulasi untuk membuat model dan mengoptimalkan risiko devisa.
-
Sears menggunakan simulasi untuk menentukan berapa banyak unit dari setiap lini produk yang harus dipesan dari pemasok—misalnya, jumlah pasang celana panjang Dockers yang harus dipesan tahun ini.
-
Perusahaan minyak dan obat menggunakan simulasi untuk menghargai "opsi nyata," seperti nilai opsi untuk memperluas, mengontrak, atau menunda proyek.
-
Perencana keuangan menggunakan simulasi Monte Carlo untuk menentukan strategi investasi yang optimal untuk masa pensiun klien mereka.
Ketika mengetikkan rumus =RAND() dalam sel, Anda akan mendapatkan angka yang sama-sama mungkin mengasumsikan nilai apa pun antara 0 dan 1. Jadi, sekitar 25 persen dari waktu, Anda harus mendapatkan angka yang kurang dari atau sama dengan 0,25; sekitar 10 persen dari waktu Anda harus mendapatkan angka yang setidaknya 0,90, dan seterunya. Untuk menunjukkan cara kerja fungsi RAND, lihat Randdemo.xlsx file, yang diperlihatkan dalam Gambar 60-1.
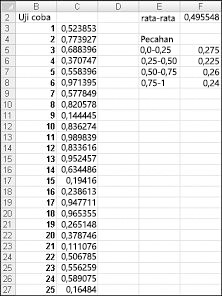
Catatan: Ketika membuka file Randdemo.xlsx, Anda tidak akan melihat angka acak yang sama yang diperlihatkan dalam Gambar 60-1. Fungsi RAND selalu menghitung ulang angka yang dihasilkannya secara otomatis saat lembar kerja dibuka atau ketika informasi baru dimasukkan ke dalam lembar kerja.
Pertama, salin dari sel C3 ke C4:C402 rumus =RAND(). Lalu beri nama rentang C3:C402 Data. Lalu, di kolom F, Anda bisa melacak rata-rata dari 400 angka acak (sel F2) dan menggunakan fungsi COUNTIF untuk menentukan pecahan antara 0 dan 0,25, 0,25 dan 0,50, 0,50 dan 0,75, dan 0,75 dan 1. Saat Anda menekan tombol F9, angka acak dihitung ulang. Perhatikan bahwa rata-rata angka 400 selalu sekitar 0,5, dan bahwa sekitar 25 persen dari hasil berada dalam interval 0,25. Hasil ini konsisten dengan definisi bilangan acak. Perhatikan juga bahwa nilai yang dihasilkan oleh RAND dalam sel yang berbeda bersifat independen. Misalnya, jika angka acak yang dihasilkan di sel C3 adalah angka yang besar (misalnya, 0,99), angka acak tidak memberi tahu kita apa pun tentang nilai angka acak lainnya yang dihasilkan.
Misalkan permintaan untuk kalender diatur oleh variabel acak diskrit berikut:
|
Permintaan |
Probabilitas |
|
10.000 |
0,10 |
|
20.000 |
0.35 |
|
40,000 |
0,3 |
|
60.000.000 |
0,25 |
Bagaimana kita bisa memainkan Excel, atau mensimulasikan, permintaan kalender ini berkali-kali? Caranya adalah dengan mengaitkan setiap kemungkinan nilai fungsi RAND dengan kemungkinan permintaan kalender. Tugas berikut memastikan bahwa permintaan 10.000 akan terjadi 10 persen dari waktu, dan seterusnya.
|
Permintaan |
Angka acak yang ditetapkan |
|
10.000 |
Kurang dari 0,10 |
|
20.000 |
Lebih besar dari atau sama dengan 0,10, dan kurang dari 0,45 |
|
40,000 |
Lebih besar dari atau sama dengan 0,45, dan kurang dari 0,75 |
|
60.000.000 |
Lebih besar dari atau sama dengan 0,75 |
Untuk menunjukkan simulasi permintaan, lihat Discretesim.xlsx file, yang diperlihatkan dalam Gambar 60-2 di halaman berikutnya.
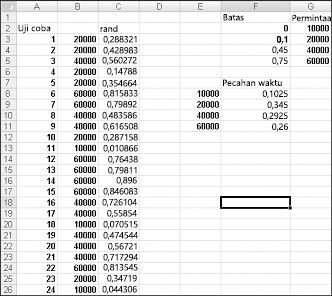
Kunci simulasi kami adalah menggunakan angka acak untuk memulai pencarian dari rentang tabel F2:G5 ( pencarian bernama). Angka acak yang lebih besar dari atau sama dengan 0 dan kurang dari 0,10 akan menghasilkan permintaan 10.000; angka acak yang lebih besar dari atau sama dengan 0,10 dan kurang dari 0,45 akan menghasilkan permintaan 20.000; angka acak yang lebih besar dari atau sama dengan 0,45 dan kurang dari 0,75 akan menghasilkan permintaan 40.000; dan angka acak yang lebih besar dari atau sama dengan 0,75 akan menghasilkan permintaan 60.000. Anda menghasilkan 400 angka acak dengan menyalin dari C3 ke C4:C402 rumus RAND(). Anda kemudian menghasilkan 400 percobaan, atau perulangan, permintaan kalender dengan menyalin dari B3 ke B4:B402 rumus VLOOKUP(C3,lookup,2). Rumus ini memastikan bahwa angka acak yang kurang dari 0,10 menghasilkan permintaan 10.000, angka acak apa pun antara 0,10 dan 0,45 menghasilkan permintaan 20.000, dan seterusnya. Dalam rentang sel F8:F11, gunakan fungsi COUNTIF untuk menentukan pecahan dari 400 perulangan kami yang menghasilkan setiap permintaan. Ketika kami menekan F9 untuk menghitung ulang angka acak, simulasi probabilitas mendekati probabilitas permintaan kami yang diasumsikan.
Jika Anda mengetik dalam sel apa pun rumus NORMINV(rand(),mu,sigma), Anda akan menghasilkan nilai simulasi dari variabel acak normal yang memiliki mu rata-rata dan sigma simpangan baku. Prosedur ini diilustrasikan dalam file Normalsim.xlsx, diperlihatkan dalam Gambar 60-3.
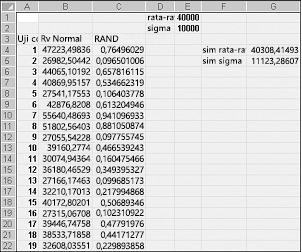
Anggaplah kita ingin mensimulasikan 400 percobaan, atau perulangan, untuk variabel acak normal dengan rata-rata 40.000 dan simpangan baku 10.000. (Anda dapat mengetikkan nilai ini dalam sel E1 dan E2, serta memberi nama nilai rata-rata dan sigma sel ini.) Menyalin rumus =RAND() dari C4 ke C5:C403 menghasilkan 400 angka acak yang berbeda. Menyalin dari B4 ke B5:B403 rumus NORMINV(C4,mean,sigma) menghasilkan 400 nilai uji coba berbeda dari variabel acak normal dengan rata-rata 40.000 dan simpangan baku 10.000. Ketika kita menekan tombol F9 untuk menghitung ulang angka acak, rata-rata tetap mendekati 40.000 dan simpangan baku mendekati 10.000.
Pada dasarnya, untuk angka acak x, rumus NORMINV(p,mu,sigma) menghasilkan persentil pth dari variabel acak normal dengan rata-rata mu dan sigma simpangan baku. Misalnya, angka acak 0,77 di sel C4 (lihat Gambar 60-3) dihasilkan di sel B4 kira-kira persentil ke-77 dari variabel acak normal dengan rata-rata 40.000 dan simpangan baku 10.000.
Di bagian ini, Anda akan melihat bagaimana simulasi Monte Carlo dapat digunakan sebagai alat pembuat keputusan. Misalkan bahwa permintaan untuk kartu Hari Valentine diatur oleh variabel acak diskrit berikut:
|
Permintaan |
Probabilitas |
|
10.000 |
0,10 |
|
20.000 |
0.35 |
|
40,000 |
0,3 |
|
60.000.000 |
0,25 |
Kartu ucapan dijual seharga $4,00, dan biaya variabel produksi setiap kartu adalah $1,50. Kartu sisa harus dibuang dengan biaya $0,20 per kartu. Berapa banyak kartu yang harus dicetak?
Pada dasarnya, kami mensimulasikan setiap kemungkinan jumlah produksi (10.000, 20.000, 40.000, atau 60.000) berkali-kali (misalnya, 1000 perulangan). Kemudian kami menentukan kuantitas pesanan mana yang menghasilkan laba rata-rata maksimum dari 1000 perulangan. Anda dapat menemukan data untuk bagian ini dalam Valentine.xlsx file, yang diperlihatkan dalam Gambar 60-4. Anda menetapkan nama rentang di sel B1:B11 ke sel C1:C11. Rentang sel G3:H6 ditetapkan pencarian nama. Parameter harga dan biaya penjualan kami dimasukkan dalam sel C4:C6.

Anda dapat memasukkan kuantitas produksi uji coba (40.000 dalam contoh ini) di sel C1. Berikutnya, buat angka acak di sel C2 dengan rumus =RAND(). Seperti yang dijelaskan sebelumnya, Anda mensimulasikan permintaan kartu di sel C3 dengan rumus VLOOKUP(rand,lookup,2). (Dalam rumus VLOOKUP, rand adalah nama sel yang ditetapkan ke sel C3, bukan fungsi RAND.)
Jumlah unit yang terjual lebih kecil dari jumlah produksi dan permintaan kami. Di sel C8, Anda menghitung pendapatan kami dengan rumus MIN(diproduksi,permintaan)*unit_price. Di sel C9, Anda menghitung total biaya produksi dengan rumus yang dihasilkan*unit_prod_cost.
Jika kami memproduksi lebih banyak kartu daripada yang diminati, jumlah unit yang tersisa sama dengan permintaan minus produksi; jika tidak, tidak ada unit yang tersisa. Kami menghitung biaya pembuangan kami di sel C10 dengan rumus unit_disp_cost*IF(menghasilkan permintaan>,diproduksi–permintaan,0). Akhirnya, di sel C11, kami menghitung laba kami sebagai pendapatan – total_var_cost-total_disposing_cost.
Kami ingin cara yang efisien untuk menekan F9 berkali-kali (misalnya, 1000) untuk setiap kuantitas produksi dan meratakan laba kami yang diharapkan untuk setiap kuantitas. Situasi ini adalah salah satu di mana tabel data dua arah datang untuk menyelamatkan kami. (Lihat Bab 15, "Analisis Sensitivitas dengan Tabel Data," untuk detail tentang tabel data.) Tabel data yang digunakan dalam contoh ini diperlihatkan dalam Gambar 60-5.
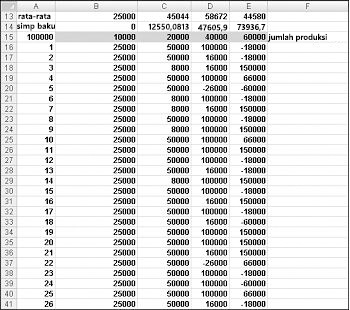
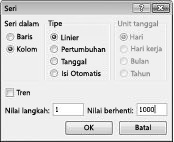
Dalam rentang sel A16:A1015, masukkan angka 1–1000 (terkait dengan 1000 percobaan kami). Salah satu cara mudah untuk membuat nilai ini adalah dengan memasukkan 1 di sel A16. Pilih sel, lalu pada tab Beranda dalam grup Pengeditan , klik Isian, dan pilih Seri untuk menampilkan kotak dialog Seri . Dalam kotak dialog Seri , diperlihatkan dalam Gambar 60-6, masukkan Nilai Langkah 1 dan Nilai Berhenti 1000. Di area Seri Di , pilih opsi Kolom , lalu klik OK. Angka 1–1000 akan dimasukkan di kolom A dimulai dari sel A16.
Selanjutnya, kami memasukkan kemungkinan jumlah produksi (10.000, 20.000, 40.000, 60.000) dalam sel B15:E15. Kami ingin menghitung laba untuk setiap angka percobaan (1 hingga 1000) dan setiap kuantitas produksi. Kami merujuk ke rumus untuk profit (dihitung dalam sel C11) di sel kiri atas tabel data kami (A15) dengan memasukkan =C11.
Kami sekarang siap untuk mengelabui Excel untuk mensimulasikan 1000 perulangan permintaan untuk setiap kuantitas produksi. Pilih rentang tabel (A15:E1014), lalu dalam grup Alat Data pada tab Data, klik Analisis Bagaimana Jika, lalu pilih Tabel Data. Untuk menyiapkan tabel data dua arah, pilih jumlah produksi kami (sel C1) sebagai Sel Input Baris dan pilih sel kosong apa pun (kami memilih sel I14) sebagai Sel Input Kolom. Setelah mengklik OK, Excel mensimulasikan 1000 nilai permintaan untuk setiap jumlah pesanan.
Untuk memahami mengapa hal ini berfungsi, pertimbangkan nilai yang ditempatkan oleh tabel data dalam rentang sel C16:C1015. Untuk setiap sel ini, Excel akan menggunakan nilai 20.000 di sel C1. Di C16, nilai sel input kolom 1 ditempatkan di sel kosong dan angka acak di sel C2 menghitung ulang. Laba terkait kemudian dicatat di sel C16. Lalu nilai input sel kolom 2 ditempatkan di sel kosong, dan angka acak di C2 kembali menghitung ulang. Laba terkait dimasukkan dalam sel C17.
Dengan menyalin dari sel B13 ke C13:E13 rumus AVERAGE(B16:B1015), kami menghitung laba simulasi rata-rata untuk setiap kuantitas produksi. Dengan menyalin dari sel B14 ke C14:E14 rumus STDEV(B16:B1015), kami menghitung simpangan baku laba simulasi kami untuk setiap kuantitas pesanan. Setiap kali kami menekan F9, 1000 perulangan permintaan disimulasikan untuk setiap jumlah pesanan. Menghasilkan 40.000 kartu selalu menghasilkan laba terbesar yang diharapkan. Oleh karena itu, tampaknya memproduksi 40.000 kartu adalah keputusan yang tepat.
Dampak Risiko terhadap Keputusan Kami Jika kami memproduksi 20.000, bukan 40.000 kartu, laba kami yang diharapkan turun sekitar 22 persen, tetapi risiko kami (sebagaimana diukur oleh simpangan baku laba) turun hampir 73 persen. Oleh karena itu, jika kita sangat terbalik dengan risiko, menghasilkan 20.000 kartu mungkin merupakan keputusan yang tepat. Kebetulan, memproduksi 10.000 kartu selalu memiliki simpangan baku 0 kartu karena jika kita memproduksi 10.000 kartu, kita akan selalu menjual semuanya tanpa sisa.
Catatan: Dalam buku kerja ini, opsi Penghitungan diatur ke Otomatis Kecuali Untuk Tabel. (Gunakan perintah Penghitungan dalam grup Penghitungan pada tab Rumus.) Pengaturan ini memastikan bahwa tabel data kami tidak akan dihitung ulang kecuali kami menekan F9, yang merupakan ide yang bagus karena tabel data yang besar akan memperlambat pekerjaan Anda jika menghitung ulang setiap kali Anda mengetikkan sesuatu ke lembar kerja Anda. Perhatikan bahwa dalam contoh ini, setiap kali Anda menekan F9, rata-rata laba akan berubah. Ini terjadi karena setiap kali Anda menekan F9, urutan berbeda dari 1000 angka acak digunakan untuk menghasilkan permintaan untuk setiap jumlah pesanan.
Interval Kepercayaan untuk Laba Rata-Rata Pertanyaan alami untuk ditanyakan dalam situasi ini adalah, ke dalam interval apa kita 95 persen yakin rata-rata laba akan jatuh? Interval ini disebut interval kepercayaan 95 persen untuk laba rata-rata. Interval kepercayaan 95 persen untuk rata-rata output simulasi dihitung dengan rumus berikut:
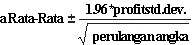
Di sel J11, Anda menghitung batas bawah untuk interval kepercayaan 95 persen terhadap laba rata-rata saat 40.000 kalender dihasilkan dengan rumus D13–1,96*D14/SQRT(1000). Di sel J12, Anda menghitung batas atas untuk interval kepercayaan 95 persen kami dengan rumus D13+1.96*D14/SQRT(1000). Perhitungan ini diperlihatkan dalam Gambar 60-7.
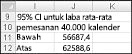
Kami 95 persen yakin bahwa laba rata-rata kami ketika 40.000 kalender yang dipesan adalah antara $56.687 dan $62.589.
-
Seorang dealer GMC percaya bahwa permintaan untuk Utusan 2005 biasanya akan didistribusikan dengan rata-rata 200 dan simpangan baku 30. Biayanya untuk menerima Utusan adalah $ 25.000, dan ia menjual Seorang Utusan seharga $ 40.000. Setengah dari semua Utusan yang tidak dijual dengan harga penuh dapat dijual seharga $30.000. Dia sedang mempertimbangkan memesan 200, 220, 240, 260, 280, atau 300 Utusan. Berapa banyak yang harus dia pesan?
-
Supermarket kecil mencoba menentukan berapa banyak salinan majalah Orang yang harus mereka pesan setiap minggu. Mereka percaya permintaan mereka untuk Orang diatur oleh variabel acak diskrit berikut:
Permintaan
Probabilitas
15
0,10
20
0.20
25
0.30
30
0,25
35
0,15
-
Supermarket membayar $ 1,00 untuk setiap salinan Orang dan menjualnya seharga $ 1,95. Setiap salinan yang belum terjual dapat dikembalikan seharga $0,50. Berapa banyak salinan Orang yang harus dipesan di toko?
Perlu bantuan lainnya?
Anda selalu dapat bertanya kepada ahli di Komunitas Teknologi Excel atau mendapatkan dukungan di Komunitas.










