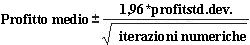Questo articolo è stato adattato da Microsoft Excel Data Analysis and Business Modeling da Wayne L. Winston.
-
Chi usa la simulazione Monte Carlo?
-
Cosa succede quando si digita =CASUALE() in una cella?
-
Come è possibile simulare i valori di una variabile casuale discreta?
-
Come è possibile simulare i valori di una variabile casuale normale?
-
In che modo una società di biglietti di auguri può determinare il numero di biglietti da produrre?
Vorremmo stimare accuratamente le probabilità di eventi incerti. Ad esempio, qual è la probabilità che i flussi di cassa di un nuovo prodotto abbiano un valore attuale netto positivo (VAN)? Qual è il fattore di rischio del nostro portafoglio di investimento? La simulazione Monte Carlo ci permette di modellare situazioni che presentano incertezza e poi di riprodurle su un computer migliaia di volte.
Nota: Il nome Monte Carlo simulazione deriva dalle simulazioni al computer eseguite durante gli anni '30 e '40 per stimare la probabilità che la reazione a catena necessaria per una bomba atomo di detonare funzionerebbe correttamente. I fisici coinvolti in questo lavoro erano grandi fan del gioco d'azzardo, così hanno dato le simulazioni il nome in codice Monte Carlo.
Nei prossimi cinque capitoli sono disponibili esempi di come è possibile utilizzare Excel per eseguire simulazioni Monte Carlo.
Molte aziende utilizzano la simulazione Monte Carlo come parte importante del loro processo decisionale. Ecco alcuni esempi.
-
General Motors, Proctor and Gamble, Pfizer, Bristol-Myers Squibb ed Eli Lilly utilizzano la simulazione per stimare sia il rendimento medio che il fattore di rischio dei nuovi prodotti. In GM, queste informazioni vengono utilizzate dal CEO per determinare quali prodotti vengono commercializzati.
-
GM utilizza la simulazione per attività quali la previsione dell'utile netto per la società, la previsione dei costi strutturali e di acquisto e la determinazione della sua suscettibilità a diversi tipi di rischio (ad esempio variazioni dei tassi di interesse e fluttuazioni dei tassi di cambio).
-
Lilly utilizza la simulazione per determinare la capacità ottimale dell'impianto per ogni farmaco.
-
Proctor e Gamble utilizzano la simulazione per modellare e coprire in modo ottimale il rischio di cambio estero.
-
Sears utilizza la simulazione per determinare quante unità di ogni linea di prodotto devono essere ordinate dai fornitori— ad esempio, il numero di coppie di pantaloni Dockers che dovrebbero essere ordinati quest'anno.
-
Compagnie farmaceutiche e petrolio utilizzano la simulazione per valutare "opzioni reali", come il valore di un'opzione per espandere, contrarre o posticipare un progetto.
-
I progettisti finanziari utilizzano la simulazione Monte Carlo per determinare strategie di investimento ottimali per il ritiro dei loro clienti.
Quando si digita la formula =CASUALE() in una cella, si ottiene un numero che è altrettanto probabile che presuppongono qualsiasi valore compreso tra 0 e 1. Pertanto, circa il 25% del tempo dovrebbe ottenere un numero minore o uguale a 0,25; circa il 10% delle volte dovresti ottenere un numero che sia almeno 0,90 e così via. Per illustrare il funzionamento della funzione CASUALE, esaminare il Randdemo.xlsx del file, illustrato nella figura 60-1.
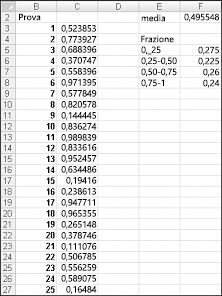
Nota: Quando si apre il file Randdemo.xlsx, gli stessi numeri casuali visualizzati nella figura 60-1 non saranno visualizzati. La funzione CASUALE ricalcola sempre automaticamente i numeri generati all'apertura di un foglio di lavoro o quando nel foglio di lavoro vengono immesse nuove informazioni.
Prima di tutto, copiare dalla cella C3 a C4:C402 la formula =CASUALE(). Assegnare quindi all'intervallo il nome Dati C3:C402. Quindi, nella colonna F è possibile tenere traccia della media dei 400 numeri casuali (cella F2) e usare la funzione CONTA.SE per determinare le frazioni compresi tra 0 e 0,25, 0,25 e 0,50, 0,50 e 0,75 e 0,75 e 1. Quando si preme il tasto F9, i numeri casuali vengono ricalcolati. Si noti che la media dei 400 numeri è sempre di circa 0,5 e che circa il 25% dei risultati è in intervalli di 0,25. Questi risultati sono coerenti con la definizione di un numero casuale. Si noti inoltre che i valori generati dalla funzione CASUALE in celle diverse sono indipendenti. Ad esempio, se il numero casuale generato nella cella C3 è un numero elevato (ad esempio 0,99), non indica nulla sui valori degli altri numeri casuali generati.
Si supponga che la domanda per un calendario sia disciplinata dalla seguente variabile casuale discreta:
|
Domanda |
Probabilità |
|---|---|
|
10.000 |
0,10 |
|
20.000 |
0,35 |
|
40,000 |
0,3 |
|
60.000 |
0,25 |
Come è possibile che Excel eserci, o simulare, questa richiesta di calendari molte volte? Il trucco consiste nell'associare ogni valore possibile della funzione CASUALE a una possibile richiesta di calendari. L'assegnazione seguente assicura che una richiesta di 10.000 avverrà il 10% del tempo e così via.
|
Domanda |
Numero casuale assegnato |
|---|---|
|
10.000 |
Minore di 0,10 |
|
20.000 |
Maggiore o uguale a 0,10 e minore di 0,45 |
|
40,000 |
Maggiore o uguale a 0,45 e minore di 0,75 |
|
60.000 |
Maggiore o uguale a 0,75 |
Per dimostrare la simulazione della domanda, esaminare il file Discretesim.xlsx, illustrato nella figura 60-2 nella pagina successiva.
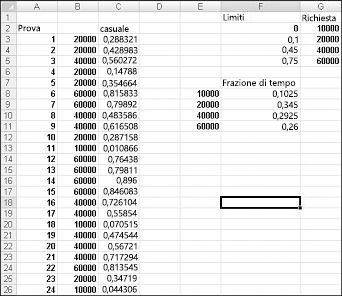
La chiave per la simulazione consiste nell'usare un numero casuale per avviare una ricerca dall'intervallo di tabelle F2:G5 ( ricerca denominata). I numeri casuali maggiori o uguali a 0 e minori di 0,10 produranno una domanda di 10.000; i numeri casuali maggiori o uguali a 0,10 e minori di 0,45 produranno una domanda di 20.000; i numeri casuali maggiori o uguali a 0,45 e minori di 0,75 produranno una domanda di 40.000; e i numeri casuali maggiori o uguali a 0,75 produranno una domanda di 60.000. Per generare 400 numeri casuali, copiare da C3 a C4:C402 la formula CASUALE(). Generare quindi 400 versioni di valutazione, o iterazioni, della domanda di calendario copiando da B3 a B4:B402 la formula CERCA.VERT(C3;ricerca;2). Questa formula assicura che qualsiasi numero casuale minore di 0,10 generi una domanda di 10.000, qualsiasi numero casuale compreso tra 0,10 e 0,45 genera una domanda di 20.000 e così via. Nell'intervallo di celle F8:F11 usare la funzione CONTA.SE per determinare la frazione delle 400 iterazioni che recedono ogni domanda. Quando premiamo F9 per ricalcolare i numeri casuali, le probabilità simulate sono vicine alle nostre presunti probabilità di domanda.
Se si digita in una cella qualsiasi la formula INV.NORM(casuale(),mu,sigma), verrà generato un valore simulato di una variabile casuale normale con un valore mu medio e una deviazione standard sigma. Questa procedura è illustrata nel file Normalsim.xlsx, illustrato nella figura 60-3.
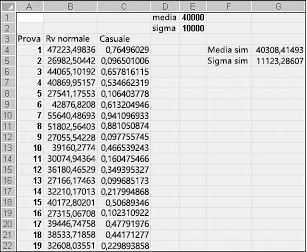
Si supponga di voler simulare 400 prove, o iterazioni, per una variabile casuale normale con una media di 40.000 e una deviazione standard di 10.000. È possibile digitare questi valori nelle celle E1 ed E2 e assegnare a queste celle il nome media e sigma, rispettivamente. La copia della formula =CASUALE() da C4 a C5:C403 genera 400 numeri casuali diversi. Copiando da B4 a B5:B403 la formula INV.NORM(C4,media,sigma) genera 400 valori di prova diversi da una variabile casuale normale con una media di 40.000 e una deviazione standard di 10.000. Quando si preme F9 per ricalcolare i numeri casuali, la media rimane vicina a 40.000 e la deviazione standard si avvicina a 10.000.
Essenzialmente, per un numero casuale x, la formula INV.NORM(p,mu,sigma) genera il pesimo percentile di una variabile casuale normale con un mu medio e una deviazione standard sigma. Ad esempio, il numero casuale 0,77 nella cella C4 (vedere figura 60-3) genera nella cella B4 circa il 77° percentile di una variabile casuale normale con una media di 40.000 e una deviazione standard di 10.000.
In questa sezione si vedrà come la simulazione Monte Carlo può essere utilizzata come strumento decisionale. Si supponga che la richiesta di una scheda di San Valentino sia disciplinata dalla seguente variabile casuale discreta:
|
Domanda |
Probabilità |
|---|---|
|
10.000 |
0,10 |
|
20.000 |
0,35 |
|
40,000 |
0,3 |
|
60.000 |
0,25 |
Il biglietto viene venduto a $ 4,00 e il costo variabile della produzione di ogni biglietto è di $ 1,50. Le carte rimanenti devono essere eliminate al costo di $ 0,20 per carta. Quante schede devono essere stampate?
In pratica, viene simulata più volte ogni quantità di produzione possibile (10.000, 20.000, 40.000 o 60.000) (ad esempio, 1000 iterazioni). Determina quindi quale quantità di ordini corrisponde al profitto medio massimo sulle 1000 iterazioni. I dati di questa sezione sono disponibili nella Valentine.xlsx file, illustrata nella figura 60-4. Assegnare i nomi degli intervalli nelle celle B1:B11 alle celle C1:C11. All'intervallo di celle G3:H6 viene assegnata la ricerca del nome. I parametri relativi a prezzo di vendita e costo vengono immessi nelle celle C4:C6.
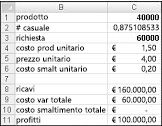
È possibile immettere una quantità di produzione di prova (40.000 in questo esempio) nella cella C1. Creare quindi un numero casuale nella cella C2 con la formula =CASUALE(). Come descritto in precedenza, si simula la domanda per la scheda nella cella C3 con la formula CERCA.VERT(casuale;ricerca;2). Nella formula CERCA.VERT rand è il nome della cella assegnata alla cella C3, non la funzione CASUALE.
Il numero di unità vendute è il minore della nostra quantità di produzione e della nostra domanda. Nella cella C8 i ricavi vengono calcolati con la formula MIN(prodotto,domanda)*unit_price. Nella cella C9 si calcola il costo di produzione totale con la formula prodotta*unit_prod_cost.
Se produciamo più carte di quante ne sono richieste, il numero di unità lasciate su è uguale alla produzione meno domanda; in caso contrario non vengono lasciate unità. Il costo di smaltimento calcolato nella cella C10 viene calcolato con la formula unit_disp_cost*SE(prodotto>domanda;prodotto-domanda;0). Infine, nella cella C11 il profitto viene calcolato come ricavi, total_var_cost-total_disposing_cost.
Vorremmo un modo efficiente per premere F9 molte volte (ad esempio, 1000) per ogni quantità di produzione e il profitto previsto per ogni quantità. Questa situazione è quella in cui una tabella dati bidirezionale viene a salvarci. Per informazioni dettagliate sulle tabelle dati, vedere il capitolo 15 "Analisi della riservatezza con tabelle dati". La tabella dati usata in questo esempio è illustrata nella figura 60-5.
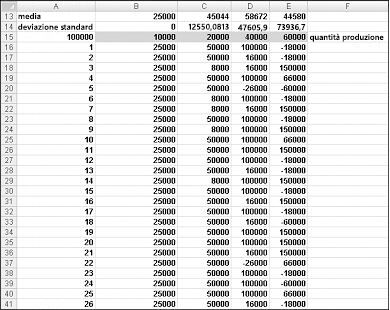
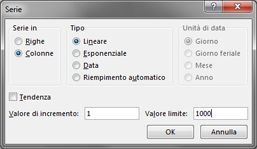
Nell'intervallo di celle A16:A1015 immettere i numeri da 1 a 1000 (corrispondenti alle 1000 prove). Un modo semplice per creare questi valori consiste nell'immettere 1 nella cella A16. Selezionare la cella, quindi nel gruppo Modifica della scheda Home fare clic su Riempimento e selezionare Serie per visualizzare la finestra di dialogo Serie. Nella finestra di dialogo Serie , illustrata nella figura 60-6, immettere un valore di incremento pari a 1 e un valore di interruzione pari a 1000. Nell'area Serie in selezionare l'opzione Colonne e quindi fare clic su OK. I numeri da 1 a 1000 verranno immessi nella colonna A a partire dalla cella A16.
Immettere quindi le quantità di produzione possibili (10.000, 20.000, 40.000, 60.000) nelle celle B15:E15. Si vuole calcolare il profitto per ogni numero di prova (da 1 a 1000) e per ogni quantità di produzione. Si fa riferimento alla formula del profitto, calcolata nella cella C11, nella cella superiore sinistra della tabella dati (A15) immettendo =C11.
Ora siamo pronti per indurre Excel a simulare 1000 iterazioni della domanda per ogni quantità di produzione. Selezionare l'intervallo di tabelle (A15:E1014) e quindi nel gruppo Strumenti dati della scheda Dati fare clic su Analisi di simulazione e quindi selezionare Tabella dati. Per impostare una tabella dati bidirezionale, scegliere la quantità di produzione (cella C1) come cella di input riga e selezionare una cella vuota (è stata scelta la cella I14) come cella di input per colonna. Dopo aver fatto clic su OK, Excel simula 1000 valori di domanda per ogni quantità di ordine.
Per capire perché funziona, considerare i valori inseriti dalla tabella dati nell'intervallo di celle C16:C1015. Per ognuna di queste celle, Excel userà un valore pari a 20.000 nella cella C1. In C16 il valore della cella di input della colonna 1 viene inserito in una cella vuota e il numero casuale nella cella C2 viene ricalcolato. Il profitto corrispondente viene quindi registrato nella cella C16. Il valore di input della cella di colonna 2 viene quindi inserito in una cella vuota e il numero casuale in C2 viene ricalcolato di nuovo. Il profitto corrispondente viene immesso nella cella C17.
Copiando dalla cella B13 a C13:E13 la formula MEDIA(B16:B1015), viene calcolato il profitto simulato medio per ogni quantità di produzione. Copiando dalla cella B14 alla cella C14:E14 la formula DEV.ST(B16:B1015), viene calcolata la deviazione standard dei profitti simulati per ogni quantità di ordine. Ogni volta che premiamo F9, vengono simulate 1000 iterazioni della domanda per ogni quantità di ordine. Produrre 40.000 carte corrisponde sempre al profitto massimo previsto. Pertanto, sembra che produrre 40.000 carte è la decisione giusta.
L'impatto del rischio sulla nostra decisione Se abbiamo prodotto 20.000 invece di 40.000 carte, il profitto previsto diminuisce di circa il 22 per cento, ma il rischio (misurato dalla deviazione standard del profitto) diminuisce di quasi il 73%. Pertanto, se siamo estremamente contrari al rischio, produrre 20.000 carte potrebbe essere la decisione giusta. Per inciso, produrre 10.000 carte ha sempre una deviazione standard di 0 carte perché se produciamo 10.000 carte, le venderemo sempre senza lasciare.
Nota: Nella cartella di lavoro l'opzione Calcolo è impostata su Automatico ad eccezione delle tabelle. Usare il comando Calcolo nel gruppo Calcolo della scheda Formule. Questa impostazione garantisce che la tabella dati non verrà ricalcolata a meno che non si preme F9, il che è una buona idea perché una tabella dati di grandi dimensioni rallenta il lavoro se viene ricalcolato ogni volta che si digita qualcosa nel foglio di lavoro. Si noti che in questo esempio, ogni volta che si preme F9, il profitto medio cambia. Questo accade perché ogni volta che si preme F9, viene usata una diversa sequenza di 1000 numeri casuali per generare richieste per ogni quantità di ordine.
Intervallo di confidenza per il profitto medio Una domanda naturale da porre in questa situazione è, in quale intervallo siamo al 95 per cento sicuri che il vero profitto medio cadrà? Questo intervallo è denominato intervallo di confidenza del 95% per il profitto medio. Un intervallo di confidenza del 95% per la media di qualsiasi output di simulazione viene calcolato dalla formula seguente:
Nella cella J11 si calcola il limite inferiore dell'intervallo di confidenza del 95% sul profitto medio quando vengono prodotti 40.000 calendari con la formula D13-1,96*D14/RADQ(1000). Nella cella J12 si calcola il limite superiore dell'intervallo di confidenza del 95% con la formula D13+1,96*D14/RADQ(1000). Questi calcoli sono illustrati nella figura 60-7.
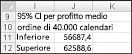
Siamo certi del 95% che il profitto medio quando vengono ordinati 40.000 calendari sia compreso tra $ 56.687 e $ 62.589.
-
Un rivenditore GMC ritiene che la domanda di inviati del 2005 sarà normalmente distribuita con una media di 200 e una deviazione standard di 30. Il suo costo di ricevere un Inviato è di $25.000 e vende un Inviato per $40.000. Metà di tutti gli Inviati non venduti a prezzo pieno possono essere venduti a $30.000. Sta pensando di ordinare 200, 220, 240, 260, 280 o 300 inviati. Quanti devono ordinare?
-
Un piccolo supermercato sta cercando di determinare quante copie di Persone rivista devono ordinare ogni settimana. Ritengono che la loro richiesta di Persone sia disciplinata dalla seguente variabile casuale distinta:
Domanda
Probabilità
15
0,10
20
0,20
25
0.30
30
0,25
35
0,15
-
Il supermercato paga $ 1,00 per ogni copia di Persone e lo vende a $ 1,95. Ogni copia invenduta può essere restituita per $ 0,50. Quante copie di Persone deve essere ordinato nello Store?
Servono altre informazioni?
È sempre possibile rivolgersi a un esperto della Tech Community di Excel o ottenere supporto nelle Community.