CONFIDENCE.NORM 함수

설명

신뢰 간격은 값의 범위입니다. 샘플 평균 x는 이 범위의 중심에 있으며 범위는 ± CONFIDENCE.NORM입니다. 예를 들어 x가 메일을 통해 주문된 제품의 배달 시간의 샘플 평균인 경우 x ± 자신감입니다. NORM은 인구 범위입니다. 모든 채우기 평균의 경우, μ0, 이 범위에서 샘플을 얻을 확률은 x보다 μ0에서 더 크다. 모든 채우기 평균의 경우 μ0이 아닌 이 범위에서 샘플을 얻을 확률은 x보다 μ0보다 더 작습니다. 즉, x, standard_dev 및 크기를 사용하여 인구 평균이 μ0인 가설의 유의 수준 알파에서 두 개의 꼬리 테스트를 구성하는 것으로 가정합니다. 그런 다음 μ0가 신뢰 간격에 있는 경우 해당 가설을 거부하지 않습니다. μ0가 신뢰 간격에 있지 않은 경우 해당 가설을 거부합니다. 신뢰 간격은 다음 패키지가 신뢰 간격에 있는 배달 시간이 걸릴 확률 1 - 알파가 있다는 유추할 수 없습니다.

구문

CONFIDENCE.NORM(alpha,standard_dev,size)

CONFIDENCE.NORM 함수 구문에는 다음과 같은 인수가 사용됩니다.

• alpha     필수 요소입니다. 신뢰 수준을 계산하는 데 사용되는 중요도 수준입니다. 신뢰 수준은 100*(1 - alpha)%이나, 즉 알파 0.05는 95% 신뢰 수준을 나타냅니다.

• standard_dev     필수 요소입니다. 데이터 범위에 대한 모집단의 표준 편차로서 그 값을 알고 있다고 가정합니다.

• size     필수 요소입니다. 표본 크기입니다.

주의

• 숫자가 아닌 인수가 있으면 CONFIDENCE.NORM에서는 #VALUE! 오류 값이 반환됩니다.

• alpha ≤ 0 또는 alpha ≥ 1이면 CONFIDENCE.NORM에서는 #NUM! 오류 값이 반환됩니다.

• standard_dev ≤ 0이면 CONFIDENCE.NORM에서는 #NUM! 오류 값이 반환됩니다.

• size가 정수가 아니면 소수점 이하는 무시됩니다.

• size < 1이면 CONFIDENCE.NORM에서는 #NUM! 오류 값이 반환됩니다.

• alpha가 0.05라고 가정하면 표준 정규 곡선에서 (1 - alpha), 즉 95%에 해당하는 구간의 면적을 계산해야 합니다. 이 값은 ± 1.96입니다. 따라서 신뢰 구간은 다음과 같습니다.

  

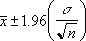
예제

다음 표의 예제 데이터를 복사하여 새 Excel 워크시트의 A1 셀에 붙여 넣습니다. 수식의 결과를 표시하려면 수식을 선택하고 F2 키를 누른 다음 Enter 키를 누릅니다. 필요한 경우 열 너비를 조정하면 데이터를 모두 표시할 수 있습니다.