LINEST (funkcija LINEST)

Aprašas

Funkcija LINEST apskaičiuoja linijos statistiką naudodama metodą "mažiausi kvadratai", kad apskaičiuotų tiesią liniją, geriausiai tinkančią jūsų duomenims, ir grąžina masyvą, apibūdinantį liniją. Taip pat galite sujungti LINEST su kitomis funkcijomis, kad apskaičiuotų kitų tipų modelių, kurie yra linijiniai nežinomuose parametruose, statistiką, įskaitant daugianominę, logaritminę, eksponentinę ir galios seką. Ši funkcija grąžina reikšmių masyvą, todėl ji turi būti įvedama kaip masyvo formulė. Instrukcijos pateikiamos šiame straipsnyje pateikiamuose pavyzdžiuose.

Tiesės lygtis yra:

y = mx + b

Arba

y = m1x1 + m2x2 + ... + b

jeigu yra keli x reikšmių diapazonai, kur priklausoma y reikšmė yra nepriklausomų x reikšmių funkcija. M reikšmės yra kiekvieną x reikšmę atitinkantys koeficientai, o b yra konstanta. Atkreipkite dėmesį, kad y, x ir m gali būti vektoriai. Masyvas, kurį grąžina funkcija LINEST, yra {mn,mn-1,...,m1,b}. LINEST taip pat gali grąžinti papildomus regresinės statistikos duomenis.

Sintaksė

LINEST(žinomi_y, [žinomi_x], [konst], [statistika])

Funkcijos LINEST sintaksė turi tokius argumentus:

Sintaksė

• žinomi_y    Būtinas. Susijęs su jau žinomų y reikšmių aibe y = mx + b.

  • Jei žinomi_y diapazonas yra viename stulpelyje, kiekvienas žinomų_x stulpelis laikomas atskiru kintamuoju.

  • Jei žinomi_y diapazonas yra vienoje eilutėje, kiekviena žinomų_x eilutė laikoma atskiru kintamuoju.

• žinomi_x    Pasirinktinis. Nebūtinai susiję su jau žinomų x reikšmių aibe y = mx + b.

  • Žinomi_x diapazone gali būti viena ar daugiau kintamųjų aibių. Jei naudojamas tik vienas kintamasis, žinomi_y ir žinomi_x gali būti bet kokios formos diapazonai, jei tik jų dimensijos sutampa. Jei naudojama daugiau nei vienas kintamasis, žinomi_y turi būti vektorius (t. y. diapazonas, kurio aukštis – viena eilutė arba plotis – vienas stulpelis).

  • Jei argumentas žinomi_x praleistas, laikoma, kad tai masyvas {1;2;3,...}, kuris yra tokio pat dydžio kaip ir žinomi_y.

• konst    Pasirinktinis. Loginė reikšmė, nurodanti, ar konstanta b turi būti lygi 0.

  • Jei konstanta yra TRUE arba praleista, b skaičiuojama įprastai.

  • Jei konstanta yra FALSE, b prilyginama 0, o m reikšmės koreguojamos taip, kad atitiktų lygybę y = mx.

• statistika    Pasirinktinis. Loginė reikšmė, nurodanti, ar reikia grąžinti papildomus regresinės statistikos duomenis.

  • Jei statistika yra TRUE (teisinga), LINEST grąžina papildomą regresinę statistiką; todėl grąžintas masyvas yra {mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r²,sey; F,df;ssreg,ssresid}.

  • Jei statistika yra FALSE arba praleista, LINEST grąžina tik m koeficientus ir konstantą b.

    Papildomos regresinės statistikos duomenys yra šie.

Ši iliustracija rodo tvarką, kuria grąžinami papildomi regresinės statistikos duomenys.

Pastabos

• Bet kokią tiesę galite aprašyti krypties koeficientu ir y postūmiu:

  Nuolydis (m):
  Norėdami rasti linijos nuolydį, dažnai rašomą kaip m, paimkite du taškus ties linija (x1,y1) ir (x2,y2); nuolydis lygus (y2 – y1)/(x2 - x1).

  Y-intercept (b):
  Y-intercept of a line, often written as b, is the value of y at the point where the line crosses the y-axis.

  Tiesės lygtis yra y = mx + b. Jei žinotei reikšmes m ir b, galite apskaičiuoti bet kokį tiesėje esantį tašką, į šią lygtį įrašydami y arba x reikšmę. Taip pat galite naudoti funkciją TREND.

• Jei turite tik vieną nepriklausomą kintamąjį x, galite gauti krypties koeficiento ir y postūmio reikšmes tiesiogiai naudodami šias formules:

  Nuolydis:
  =INDEX(LINEST(known_y,known_x's),1)

  Y-intercept:
  =INDEX(LINEST(known_y,known_x's),2)

• Funkcijos LINEST apskaičiuotos tiesės tikslumas priklauso nuo jūsų duomenų sklaidos koeficiento. Kuo tiesiškesni duomenys, tuo tikslesnis LINEST modelis. Funkcija LINEST geriausiai jūsų duomenis atitinkantį variantą parenka naudodama mažiausiųjų kvadratų metodą. Jei turite tik vieną nepriklausomą kintamąjį x, m ir b skaičiavimas pagrįstas šiomis formulėmis:

  

  

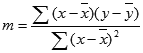
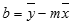
  kur x ir y yra pavyzdžio vidurkiai, t. y. x = AVERAGE(žinomi_x), o y = AVERAGE(žinomi_y).

• Linijos ir kreivės jungiamosios funkcijos LINEST ir LOGEST gali apskaičiuoti geriausią tiesią liniją arba eksponentinę kreivę, kuri atitinka jūsų duomenis. Tačiau turite nuspręsti, kuris iš dviejų rezultatų geriausiai atitinka jūsų duomenis. Galite apskaičiuoti trend(known_y,known_x' s) tiesioje linijoje arba GROWTH(known_y' s, known_x's) eksponentinės kreivės. Šios funkcijos be new_x argumento grąžina y reikšmių masyvą, prognozuojamą išilgai tos linijos arba kreivės ties faktiniais duomenų taškais. Tada galima palyginti numatomas reikšmes su faktinėmis reikšmėmis. Galite juos abu susekite į diagramą, kad būtų galima vizualiai palyginti.

• Regresinėje analizėje programa „Excel“ kiekvienam taškui randa skirtumo tarp to taško apskaičiuotos y reikšmės ir realios y reikšmės kvadratą. Šių skirtumų kvadratų suma vadinama liekamąja kvadratų suma ksliek. Tuomet programa „Excel“ apskaičiuoja bendrą kvadratų sumą ksbendra. Kai argumentas konstanta = TRUE arba praleistas, bendra kvadratų suma yra kvadratu pakeltų skirtumų tarp tikrųjų y reikšmių ir vidutinių y reikšmių suma. Kai argumentas konstanta = FALSE, bendra kvadratų suma yra kvadratu pakeltų tikrųjų y reikšmių (neatimant vidutinės y reikšmės iš kiekvienos y reikšmės) suma. Tuomet gali būti randama regresijos kvadratų suma ksreg: ksreg = ksbendra - ksliek. Kuo mažesnė liekamoji kvadratų suma, palyginti su bendra kvadratų suma, tuo didesnė nustatymo koeficiento reikšmė r 2 ,^otai rodo, kaip regresinės analizės lygtis paaiškina ryšį tarp kintamųjų. R^{2 reikšmė lygi} ssreg/sstotal.

• Kai kuriais atvejais viename ar daugiau X stulpelių (tarkime, kad Y ir X yra stulpeliuose) gali būti papildomų prognozių reikšmių, jei yra kitų X stulpelių. Kitaip tariant, pašalinus vieną ar daugiau X stulpelių, gali būti prognozuojamos Y reikšmės, kurios yra vienodai tikslios. Tokiu atveju šie pertekliniai X stulpeliai turėtų būti neįtraukti į regresijos modelį. Šis reiškinys vadinamas "kolinearumu", nes bet kurį perteklinį X stulpelį galima išreikšti kaip perteklinių X stulpelių kartotinių sumą. Funkcija LINEST tikrina, ar nėra kolinearumo, ir pašalina visus perteklinius X stulpelius iš regresijos modelio, kai juos identifikuoja. Pašalinti X stulpeliai linest išvestyje gali būti atpažįstami kaip turintys 0 koeficientų, be 0 se reikšmių. Jei vienas ar daugiau stulpelių pašalinami kaip pertekliniai, df paveikiamas, nes df priklauso nuo X stulpelių skaičiaus, faktiškai naudojamų prognozavimo tikslais. Daugiau informacijos apie df skaičiavimas, žr. 4 pavyzdys. Jei df pakeičiamas, nes pašalinami pertekliniai X stulpeliai, taip pat paveikiamos sey ir F reikšmės. Kolinearumas praktikoje turėtų būti gana retas. Tačiau vienas atvejis, kai tikėtina, kad jis atsiras, yra tada, kai kai kuriuose X stulpeliuose yra tik 0 ir 1 reikšmės kaip indikatoriai, ar eksperimento objektas yra konkrečios grupės narys, ar ne. Jei konsta = TRUE arba praleista, funkcija LINEST efektyviai įterpia papildomą X stulpelį iš visų 1 reikšmių, kad būtų galima modeliuoti perėmimą. Jei turite stulpelį su 1 kiekvienam klausimui, jei vyras, arba 0, jei ne, ir jūs taip pat turite stulpelį su 1 kiekvienam klausimui, jei moteris, arba 0, jei ne, šis stulpelis yra perteklinis, nes jo įrašus galima gauti atimant įrašą stulpelyje "vyrų indikatorius" iš įrašo papildomame stulpelyje su visomis 1 reikšmėmis, kurias įtraukė funkcija LINEST.

• Jei nė vienas X stulpelis nepašalinamas iš modelio dėl kolinearumo, ll reikšmė yra skaičiuojama taip: jei egzistuoja kžinomų_x stulpelių, o konstanta = TRUE arba praleista, ll = n – k – 1. Jei konstanta = FALSE, ll = n - k. Abiem atvejais kiekvienas X stulpelis, kuris buvo pašalintas dėl kolinearumo, padidina ll reikšmę vienetu.

• Įvesdami konstantų masyvą (pvz., žinomi_x) kaip argumentą, atskirkite toje pačioje eilutėje esančias reikšmes kableliais, o eilutes – kabliataškiais. Skyriklio simboliai gali skirtis, atsižvelgiant į regiono parametrus.

• Atkreipkite dėmesį, kad regresijos lygties prognozuojamos y reikšmės gali negalioti, jei jos yra už y reikšmių diapazono, naudoto lyčiai apibrėžti.

• Esantis algoritmas, kuris naudojamas funkcijoje LINEST, skiriasi nuo funkcijose SLOPE ir INTERCEPT naudojamo algoritmo. Dėl šių algoritmų skirtumo, kai duomenys neapibrėžti ir linijiški, rezultatai gali skirtis. Pavyzdžiui, jei argumento žinomi y duomenų taškai lygūs 0, o argumento žinomi x duomenų taškai lygūs 1:

  • Funkcijos LINEST grąžinama reikšmė lygi 0. Funkcijos LINEST algoritmas skirtas tinkamiems linijiškų duomenų rezultatams grąžinti ir tokiu atveju galima rasti mažiausiai vieną atsakymą.

  • SLOPE ir INTERCEPT grąžina #DIV/0! klaidą. Funkcijų SLOPE ir INTERCEPT algoritmas skirtas ieškoti tik vieno atsakymo, o šiuo atveju gali būti daugiau nei vienas atsakymas.

• Be to, kad funkciją LOGEST naudojate kitų regresijų tipų statistikai skaičiuoti, galite naudoti funkciją LINEST kitų regresijų tipų diapazonui skaičiuoti įvesdami x ir y kintamųjų funkcijas kaip funkcijos LINEST x ir y sekas. Pavyzdžiui ši formulė:

  =LINEST(yreikšmės, xreikšmės^STULPELIS($A:$C))

  veikia, kai norite skaičiuoti vieno y reikšmių stulpelio ir vieno x reikšmių stulpelio kubinę formos (trečios eilės polinomo) aproksimaciją:

  y = m1*x + m2*x^2 + m3*x^3 + b

  Galite keisti šią formulę kitiems regresijos tipams skaičiuoti, bet kai kuriais atvejais reikia derinti išvesties reikšmes ir kitus statistinius duomenis.

• F testo reikšmė, kurią grąžina funkcija LINEST, skiriasi nuo F testo reikšmės grąžinamos funkcijos FTEST. LINEST grąžina F statistiką, o funkcija FTEST grąžina tikimybę.

Pavyzdžiai