Šajā rakstā paskaidrota funkcijas LINEST formulas sintakse un lietošana programmā Microsoft Excel.
Apraksts
Funkcija LINEST aprēķina taisnes statistiku, izmantojot “mazāko kvadrātu” metodi ar datiem saskaņotas taisnes aprēķināšanai, un pēc tam atgriež taisni raksturojošu masīvu. Lai aprēķinātu statistiku citiem modeļu tipiem, kas nezināmajos parametros ir lineāri, ieskaitot polinoma, logaritmiskās, eksponenciālās un pakāpju sērijas, funkciju LINEST var arī kombinēt ar citām funkcijām. Šī funkcija atgriež vērtību masīvu, tāpēc tā ir jāievada kā masīva formula. Šajā rakstā pēc piemēriem ir instrukcijas.
Taisnes vienādojums ir:
y = mx + b
–vai–
y = m1x1 + m2x2 + ... + b
ja ir vairāki x vērtību diapazoni, kur atkarīgās y vērtības ir neatkarīgo x vērtību funkcija. Attiecīgi m vērtības ir katras x vērtības koeficienti un b ir konstanta vērtība. Ievērojiet, ka y, x un m var būt vektori. Funkcijas LINEST atgrieztais masīvs ir {mn,mn-1,...,m1,b}. Funkcija LINEST var atgriezt arī regresijas papildu statistiku.
Sintakse
LINEST(zināmie_y, [zināmie_x], [konst], [statist])
Funkcijas LINEST sintaksei ir šādi argumenti.
Sintakse
-
zināmie Obligāts arguments. Zināmo y vērtību kopa attiecībā y = mx + b.
-
Ja argumentu zināmie_y diapazons atrodas vienā kolonnā, tad katra zināmo_x kolonna tiek interpretēta kā atsevišķs mainīgais.
-
Ja argumentu zināmie_y diapazonu ietver viena rinda, tad katra zināmo_x rinda tiek interpretēta kā atsevišķs mainīgais.
-
-
zināmie_x Neobligāts arguments. X vērtību kopa, kura, iespējams, jau ir zināma attiecībā y = mx + b.
-
Argumentu zināmie_x diapazons var ietvert vienu vai vairākas mainīgo kopas. Ja tiek izmantots tikai viens mainīgais, zināmie_y un zināmie_x var būt jebkuras formas diapazoni, ja vien to izmēri ir vienādi. Ja tiek izmantoti vairāki mainīgie, zināmajiem_y jābūt vektoram (tas ir, diapazonam, kura augstums ir viena rinda vai kura platums ir viena kolonna).
-
Ja zināmie_x tiek izlaisti, tiek pieņemts, ka šī masīva {1,2,3,...} izmērs ir tāds pats kā zināmajiem_y.
-
-
konst Neobligāts arguments. Loģiskā vērtība, kas norāda, vai konstanti b iestatīt vienādu ar 0.
-
Ja konst ir TRUE vai izlaista, tad b tiek aprēķināta kā parasti.
-
Ja konst ir FALSE, tad b tiek iestatīta vienāda ar 0 un m vērtības tiek pielāgotas y = mx.
-
-
statist Neobligāts arguments. Loģiskā vērtība, kas norāda, vai atgriezt papildu regresijas statistiku.
-
Ja statisti ir TRUE, tad FUNKCIJA LINEST atgriež regresijas papildu statistiku. rezultātā atgrieztais masīvs ir {mn,mn-1,...,m1,b; sen,sen-1,...,se1,seb; r2,sey; F,df; ssreg,ssresid}.
-
Ja statist ir FALSE vai izlaista, tad LINEST atgriež tikai m koeficientus un konstanti b.
Regresijas papildu statistika ir šāda.
-
|
Statistika |
Apraksts |
|---|---|
|
se1,se2,...,sen |
Koeficientu m1,m2,...,mn standarta kļūdu vērtības. |
|
seb |
Konstantes b (seb = #N/A, ja konst ir FALSE) standarta kļūdas vērtība. |
|
r2 |
Noteikšanas koeficients. Salīdzina y aptuvenās vērtības ar faktiskajām un diapazonus ar vērtību no 0 līdz 1. Ja ir 1, tad piemērā ir pilnīga korelācija — nav atšķirības starp y aptuveno un faktisko vērtību. Ja otrā proporcijas malējā loceklī noteikšanas koeficients ir 0, tad y vērtības noteikšanai korelācijas vienādojums nav noderīgs. Informāciju par2. aprēķina veidu skatiet turpmāk šīs tēmas sadaļā Piebildes. |
|
sey |
Aptuvenās y vērtības standarta kļūda. |
|
F |
F statistika vai F novērotā vērtība. Izmantojiet F statistiku, lai noteiktu, vai novērotā attiecība starp atkarīgajiem un neatkarīgajiem mainīgajiem parādās nejauši. |
|
df |
Brīvības pakāpes. Izmantojiet brīvības pakāpes, lai statistikas tabulā atrastu kritiskās F vērtības. Salīdziniet tabulā atrastās vērtības ar LINEST atgriezto F statistiku, lai noteiktu modeļa ticamības līmeni. Informāciju par df aprēķinu skatiet turpmāk šīs tēmas sadaļā Piebildes. 4. piemērā parādīts F un df izmantošana. |
|
ssreg |
Kvadrātu regresijas summa. |
|
ssresid |
Kvadrātu starpības summa. Informāciju par ssreg un ssresid aprēķināšanu skatiet turpmāk šīs tēmas “Piebildēs”. |
Attēlā redzama kārtība, kādā tiek atgriezta regresijas papildu statistika.

Piebildes
-
Jebkuru taisni var raksturot ar slīpni un y krustpunktu:
Slīpums (m):
Lai atrastu līnijas slīpumu, kas bieži ierakstīts kā m, uz līnijas ir divi punkti (x1,y1) un (x2,y2); slīpums ir vienāds ar (y2 - y1)/(x2 - x1).Y krustpunkts (b):
Līnijas y krustpunkts, ko parasti raksta kā b, ir y vērtība tajā punktā, kur līnija krusto y asi.Taisnes vienādojums ir y = mx + b. Ja m un b vērtības ir zināmas, tad var aprēķināt jebkuru taisnes punktu, ievietojot vienādojumā y vai x vērtību. Var izmantot arī funkciju TREND.
-
Ja ir tikai viens neatkarīgs mainīgais x, tad iegūt slīpnes un y krustpunkta vērtības var tieši, izmantojot šādas formulas:
Slīpums:
=INDEX(LINEST(known_y;known_x);1)Y krustpunkts:
=INDEX(LINEST(known_y;known_x);2) -
Ar funkciju LINEST aprēķinātas taisnes precizitāte ir atkarīga no datu izkaisījuma pakāpes. Jo lineārāki dati, jo precīzāks funkcijas LINEST modelis. Datu vislabākā piemērojuma noteikšanai funkcija LINEST izmanto mazāko kvadrātu metodi. Ja ir tikai viens neatkarīgs mainīgais x, tad m un b aprēķini pamatojas uz šādām formulām:
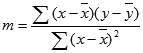
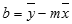
kur x un y ir piemēra vidējais, t.i., x = AVERAGE(zināmie_x) un y = AVERAGE(zināmie_y).
-
Līnijas un līkņu nogulšanas funkcijas LINEST un LOGEST var aprēķināt labāko taisno līniju vai eksponenciālo līkni, kas datiem der. Tomēr jums ir jāizlemj, kurš no diviem rezultātiem vislabāk atbilst jūsu datiem. Taisnas līnijai var aprēķināt TREND(known_y known_x known_x) vai GROWTH(known_y, known_x, known_x)eksponenciālā līknei. Šīs funkcijas bez new_x argumenta atgriež pie faktiskajiem datu punktiem prognozēto y vērtību masīvu. Pēc tam prognozētās vērtības var salīdzināt ar faktiskajām vērtībām. Iespējams, vēlēsities tos abus diagrammātēt, lai iegūtu vizuālu salīdzinājumu.
-
Regresijas analīzē programma Excel aprēķina katra punkta kvadrātisko atšķirību starp punkta aptuveno un faktisko y vērtību. Šo kvadrātisko atšķirību summu sauc par kvadrātu starpības summu ssresid. Pēc tam programma Excel aprēķina kvadrātu kopsummu sstotal. Ja arguments konst = TRUE vai izlaists, tad kvadrātu kopsumma ir faktisko un vidējo y vērtību summas kvadrātu atšķirība. Ja arguments konst = FALSE, tad kvadrātu kopsumma ir faktisko y vērtību kvadrātu summa (bez vidējās y vērtības atņemšanas no katras atsevišķas y vērtības). Tad kvadrātu regresijas summu ssreg var atrast šādi: ssreg = sstotal - ssresid. Jo mazāka ir kvadrātu starpības summa, salīdzinot ar kvadrātu kopsummu, jo lielāka ir noteikšanas koeficienta vērtība r2, kas norāda, cik labi regresijas analīzes vienādojums izskaidro mainīgo relāciju. r2 ir vienāds ar ssreg/sstotal.
-
Dažos gadījumos vienai vai vairākām X kolonnām (pieņemot, ka Y un X ir kolonnās) var būt papildu prognozējošā vērtība citu X kolonnu gadījumā. Citiem vārdiem sakot, vienas vai vairākas X kolonnas noņemšana var radīt vienmērīgi precīzas Y vērtības. Šādā gadījumā šīs liekās X kolonnas regresijas modelī ir jālaiž. Šo kolinearitāti dēvē par kolinearitāti, jo jebkuru lieko X kolonnu var izteikt kā ne redundanto X kolonnu vairākkārtņu summu. Funkcija LINEST pārbauda kolinearitāti un, identificējot lieko X kolonnu, no regresijas modeļa noņem visas liekās X kolonnas. Noņemtās X kolonnas LINEST izvadē var atpazīt kā tās ar 0 koeficientiem papildus 0 se vērtībām. Ja viena vai vairākas kolonnas tiek noņemtas kā liekas, tiek ietekmēta df, jo df ir atkarīgs no X kolonnu skaita, kas faktiski tiek izmantots prognozēšanas nolūkos. Detalizētu informāciju par df skaitļošanu skatiet 4. piemērā. Ja df tiek mainīts tāpēc, ka tiek noņemtas liekās X kolonnas, tiek ietekmētas arī sey un F vērtības. Kolinearitātei ir jābūt relatīvi reti sastopamai. Tomēr viens gadījums, kur, visticamāk, varētu rasties, ir tas, ka dažas X kolonnas satur tikai 0 un 1 vērtības kā rādītājus par to, vai tēma eksperimentā ir vai nav konkrētas grupas dalībnieks. Ja konst = TRUE vai izlaista, funkcija LINEST efektīvi ievieto papildu X kolonnu no visām 1 vērtībām, lai modelēt krustpunktu. Ja jums ir kolonna ar 1 katrai tēmai, ja vīrietis vai 0, ja tā nav, un jums ir arī kolonna ar 1 katrai tēmai, ja sieviete, vai 0, ja tā nav, šī otrā kolonna ir lieka, jo tās ierakstus var iegūt, no ieraksta atņemot ierakstu "zēnu indikatora" kolonnā no ieraksta visu 1 funkcijas LINEST pievienoto vērtību papildu kolonnā.
-
Ja kolinearitātes dēļ no modeļa netiek noņemta neviena X kolonna, tad df vērtība tiek aprēķināta šādi: ja ir zināmo_xk kolonnas un konst = TRUE vai izlaista, tad df = n – k – 1. Ja konst = FALSE, tad df = n - k. Abos gadījumos katra X kolonna, kas tika noņemta, kolinearitātes ietekmē palielina df vērtību par 1.
-
Ievadot masīva konstanti (piemēram, zināmos_x) kā argumentu, izmantojiet komatus vienā rindā esošu vērtību atdalīšanai, bet semikolus — rindu atdalīšanai. Atdalītājrakstzīmes var atšķirties atkarībā no reģionālajiem iestatījumiem.
-
Ievērojiet, ka regresijas vienādojuma iepriekš noteiktās y vērtības var nebūt derīgas, ja tās atrodas ārpus vienādojuma aprēķināšanai izmantotā y vērtību diapazona.
-
Funkcijas LINEST pamatā esošais algoritms atšķiras no funkcijās SLOPE un INTERCEPT pamatā esošā algoritma. Atšķirība starp šiem algoritmiem var novest pie atšķirīgiem rezultātiem, ja dati ir nenoteikti un kolineāri. Piemēram, ja argumenta zināmie_y datu punkti ir 0 un argumenta zināmie_x ir 1:
-
funkcija LINEST atgriež vērtību 0. Funkcijas LINEST algoritms ir paredzēts saprātīgu rezultātu atgriešanai kolineāriem datiem, un šajā gadījumā var atrast vismaz vienu atbildi.
-
SLOPE un INTERCEPT atgriež #DIV/0! Ja norādītā pozīcija atrodas pirms lauka pirmā vienuma vai aiz lauka pēdējā vienuma, formula radīs kļūdu #REF!. Funkciju SLOPE un INTERCEPT algoritms ir paredzēts tikai vienas atbildes meklējiet, un šajā gadījumā var būt vairākas atbildes.
-
-
Papildus tam, ka funkcija LOGEST tiek lietota, lai aprēķinātu statistiku citiem regresijas tipiem, funkciju LINEST var lietot, lai aprēķinātu citu regresijas tipu diapazonu, ievadot mainīgo x un y funkcijas kā x un y sērijas funkcijai LINEST. Piemēram, šāda formula:
=LINEST(yvalues, xvalues^COLUMN($A:$C))
darbojas, kad ir viena kolonna y-vērtībām un viena kolonna x-vērtībām, lai aprēķinātu formas trešās pakāpes (secības 3 polinomu) aproksimāciju:
y = m1*x + m2*x^2 + m3*x^3 + b
Lai aprēķinātu citus regresijas tipus, formulu var koriģēt, bet dažos gadījumos ir jākoriģē izvades vērtības un cita statistika.
-
F testa vērtība, ko atgriež funkcija LINEST, atšķiras no F testa vērtības, ko atgriež funkcija FTEST. LINEST atgriež statistisko F, bet FTEST atgriež varbūtību.
Piemēri
1. piemērs. Slīpne un Y krustpunkts
Nokopējiet šīs tabulas parauga datus un ielīmējiet tos jaunas Excel darblapas šūnā A1. Lai formulas parādītu rezultātus, atlasiet tos, nospiediet taustiņu F2 un pēc tam Enter. Ja nepieciešams, varat koriģēt kolonnas platumu, lai redzētu visus datus.
|
Zināmais y |
Zināmais x |
|---|---|
|
1 |
0 |
|
9 |
4 |
|
5 |
2 |
|
7 |
3 |
|
Rezultāts (slīpums) |
Rezultāts (y veida krustpunkts) |
|
2 |
1 |
|
Formula (masīva formula šūnās A7:B7) |
|
|
=LINEST(A2:A5;B2:B5;;FALSE) |
2. piemērs. Vienkārša lineāra regresija
Nokopējiet šīs tabulas parauga datus un ielīmējiet tos jaunas Excel darblapas šūnā A1. Lai formulas parādītu rezultātus, atlasiet tos, nospiediet taustiņu F2 un pēc tam Enter. Ja nepieciešams, varat koriģēt kolonnas platumu, lai redzētu visus datus.
|
Mēnesis |
Apgrozījums |
|---|---|
|
1 |
3100 € |
|
2 |
4500 € |
|
3 |
4400 € |
|
4 |
5400 € |
|
5 |
7500 € |
|
6 |
8100 € |
|
Formula |
Rezultāts |
|
=SUM(LINEST(B1:B6; A1:A6)*{9;1}) |
11 000 € |
|
Aprēķina pārdošanas novērtējumu devītajā mēnesī, pamatojoties uz 1.–6. mēneša pārdošanas datiem. |
3. piemērs. Salikta lineāra regresija
Nokopējiet šīs tabulas parauga datus un ielīmējiet tos jaunas Excel darblapas šūnā A1. Lai formulas parādītu rezultātus, atlasiet tos, nospiediet taustiņu F2 un pēc tam Enter. Ja nepieciešams, varat koriģēt kolonnas platumu, lai redzētu visus datus.
|
Platība (x1) |
Biroji (x2) |
Ieejas (x3) |
Vecums (x4) |
Noteiktā vērtība (y) |
|---|---|---|---|---|
|
2310 |
2 |
2 |
20 |
142 000 € |
|
2333 |
2 |
2 |
12 |
144 000 € |
|
2356 |
3 |
1,5 |
33 |
151 000 € |
|
2379 |
3 |
2 |
43 |
150 000 € |
|
2402 |
2 |
3 |
53 |
139 000 € |
|
2425 |
4 |
2 |
23 |
169 000 € |
|
2448 |
2 |
1,5 |
99 |
126 000 € |
|
2471 |
2 |
2 |
34 |
142 900 € |
|
2494 |
3 |
3 |
23 |
163 000 € |
|
2517 |
4 |
4 |
55 |
169 000 € |
|
2540 |
2 |
3 |
22 |
149 000 € |
|
-234,2371645 |
||||
|
13,26801148 |
||||
|
0,996747993 |
||||
|
459,7536742 |
||||
|
1732393319 |
||||
|
Formula (šūnā A19 ievadīta dinamiska masīva formula) |
||||
|
=LINEST(E2:E12;A2:D12;TRUE;TRUE) |
4. piemērs. F un r2 statistikas izmantošana
Iepriekšējā piemērā noteikšanas koeficients jeb r2 ir 0,99675 (skatiet LINEST izvades šūnu A17), kas norādīs uz stingru attiecību starp neatkarīgajiem mainīgajiem un pārdošanas cenu. Šo F statistiku var izmantot, lai noteiktu, vai rezultāti, piemēram, augsta r2 vērtība, ir parādījušies nejauši.
Pieņemsim, ka starp mainīgajiem faktiski nav saistības un uzzīmētais 11 biroju ēku neparastais piemērs liek statistiskajai analīzei rādīt stipru saikni. Varbūtībai, ka kļūdaini tiek pieņemta neesoša attiecība, tiek izmantots termins “Alpha”.
Funkcijas LINEST izvades F un df vērtības var izmantot, lai novērtētu augstākas F vērtības rašanās iespējamību nejauši. F var salīdzināt ar kritiskajām vērtībām publicētās F sadales tabulās vai funkciju FDIST programmā Excel var izmantot, lai aprēķinātu lielākas F vērtības varbūtību nejauši. Atbilstošais F sadalījums ir v1 un v2 brīvības pakāpes. Ja n ir datu punktu skaits un konst = TRUE vai izlaists, tad v1 = n – df – 1 un v2 = df. (Ja konst = FALSE, tad v1 = n – df un v2 = df.) Funkcija FDIST ar sintaksi FDIST(F,v1,v2) atgriež augstākas F vērtības varbūtību, kas parādās nejauši. Šajā piemērā df = 6 (šūna B18) un F = 459,753674 (šūna A18).
Pieņemot, ka alfa vērtība ir 0,05, v1 = 11 – 6 – 1 = 4 un v2 = 6, F kritiskais līmenis ir 4,53. Tā kā F = 459,753674 ir ievērojami lielāks par 4,53, maz ticams, ka šī lielā F vērtība radās nejauši. (Izmantojot alpha = 0,05, hipotēze, ka starp known_y un known_x ir jānoraida, ja F pārsniedz kritisko līmeni 4,53.) Funkciju FDIST programmā Excel var izmantot, lai iegūtu varbūtību, ka šī lielā F vērtība radās nejauši. Piemēram, FDIST(459,753674, 4, 6) = 1,37E-7, ļoti maza varbūtība. Var pabeigt, atrodot tabulas F kritisko līmeni vai izmantojot funkciju FDIST , ka regresijas vienādojums ir noderīgs šajā apgabalā biroju ēku vērtības noteikšanai. Atcerieties, ka ir kritiski svarīgi izmantot pareizās vērtības v1 un v2, kas tika aprēķinātas iepriekšējā rindkopā.
5. piemērs. t statistikas aprēķināšana
Cits pieņēmuma tests noteiks, vai katrs slīpnes koeficients ir noderīgs 3. piemērā biroju ēku vērtības noteikšanai. Piemēram, lai pārbaudītu vecuma koeficientu statistiskam būtiskumam, izdaliet -234,24 (vecuma slīpnes koeficientu) ar 13,268 (šūnas A15 vecuma koeficientu aptuvenā standarta kļūda). T novērotā vērtība ir šāda:
t = m4 ÷ se4 = -234.24 ÷ 13.268 = -17.7
Ja t absolūtā vērtība ir pietiekami liela, tad var secināt, ka slīpnes koeficients ir noderīgs 3. piemērā minēto biroju ēku vērtības noteikšanai. Šajā tabulā parādītas 4 t novēroto vērtību absolūtās vērtības.
Aplūkojot tabulu statistikas rokasgrāmatā, redzēsit, ka divpusējs kritiskais t ar 6 brīvības pakāpēm un Alpha = 0,05 ir 2,447. Šo kritisko vērtību var atrast arī, izmantojot programmas Excel funkciju TINV. TINV(0,056) = 2,447. t absolūtās vērtības (17,7) dēļ, kas ir lielāka par 2,447, vecums ir svarīgs mainīgais biroju ēku vērtības noteikšanai. Līdzīgi var pārbaudīt jebkuru citu neatkarīga mainīgā statistisko nozīmību. Turpmāk norādītas t novērotās vērtības katram neatkarīgam mainīgajam.
|
Mainīgais |
t novērotā vērtība |
|---|---|
|
Platība |
5.1 |
|
Biroju skaits |
31.3 |
|
Ieeju skaits |
4.8 |
|
Vecums |
17.7 |
Visām šīm vērtībām absolūtā vērtība ir lielāka par 2.447; tāpēc visi korelācijas vienādojumā izmantotie mainīgie ir noderīgi šajā rajonā esošo biroju ēku vērtības noteikšanai.










