Obs!: Vi ønsker å gi deg det nyeste hjelpeinnholdet så raskt som mulig, på ditt eget språk. Denne siden er oversatt gjennom automatisering og kan inneholde grammatiske feil eller unøyaktigheter. Formålet vårt er at innholdet skal være nyttig for deg. Kan du fortelle oss om informasjonen var nyttig for deg nederst på denne siden? Her er den engelske artikkelen for enkel referanse.
Denne artikkelen handler om hvordan du bruker problem løser, et tilleggs program fra Microsoft Excel som du kan bruke for hva-skjer-hvis-analyse for å finne en optimal produkt blanding.
Hvordan kan jeg fastslå den månedlige produkt blandingen som gir størst mulig fortjeneste?
Bedrifter må ofte bestemme hvor mye av hvert produkt som skal produseres på månedlig basis. I sin enkleste form omfatter produkt sammensetnings problemet hvordan du bestemmer hvor mye av hvert produkt som skal produseres i løpet av en måned for å maksimere fortjenesten. Produkt sammensetningen må vanligvis være i henhold til følgende betingelser:
-
Produkt sammensetningen kan ikke bruke flere ressurser enn det som er tilgjengelig.
-
Det er et begrenset behov for hvert produkt. Vi kan ikke produsere mer av et produkt i løpet av en måned enn etterspørsel, fordi den overflødige produksjonen er bortkastet (for eksempel et perishable legemiddel).
La oss nå løse følgende eksempel på produkt sammensetnings problemet. Du kan finne løsningen på dette problemet i filen prodmix. xlsx, som vises i figur 27-1.
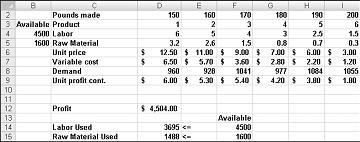
La oss si at vi jobber for et farmasøytisk firma som produserer seks forskjellige produkter i planten. Produksjonen av hvert produkt krever arbeid og råmateriale. Rad 4 i figur 27-1 viser hvor mange arbeids timer som trengs for å produsere et pund av hvert produkt, og rad 5 viser hvor mye rå varen som trengs for å produsere et nummer for hvert produkt. Hvis du for eksempel skal produsere et nummer på produkt 1, må du ha seks timer med arbeid og 3,2 pund med rå materiell. Prisen per pund er gitt for hvert legemiddel i rad 6, enhets kostnaden per pund er angitt i rad 7, og fortjeneste bidraget per pund er gitt i rad 9. Produkt 2 selger for eksempel for $11,00 per pund, som er en enhets kostnad på $5,70 per pund, og bidrar med $5,30 fortjeneste per pund. Månedens behov for hvert legemiddel er gitt i rad 8. Etterspørselen etter produkt 3 er for eksempel 1041 pund. Denne måneden er 4500 timer med arbeid og 1600 pund av rå varer tilgjengelig. Hvordan kan dette firmaet gi den månedlige fortjenesten størst mulig?
Hvis vi visste ingenting om problem løseren i Excel, vil vi angripe dette problemet ved å lage et regne ark til å spore fortjeneste-og ressurs bruk som er knyttet til produkt blandingen. Deretter bruker vi prøve perioden og feilen til å variere produkt blandingen for å optimalisere fortjeneste uten å bruke mer arbeids kraft eller rå varer enn det som er tilgjengelig, og uten å måtte produsere noe legemiddel i tillegg til behov. Vi bruker problem løseren i denne prosessen bare på prøve-og-feil-trinnet. Problem løseren er hovedsakelig en optimaliserings motor som utfører prøve perioden og feil søking.
En nøkkel for å løse produkt sammensetnings problemet er å effektivt beregne ressurs bruken og fortjenesten som er knyttet til en gitt produkt blanding. Et viktig verktøy vi kan bruke til å utføre denne beregningen er Summer produkt-funksjonen. Summer produkt-funksjonen multipliserer tilsvarende verdier i celle områder og returnerer summen av disse verdiene. Hvert celle område som brukes i en Summer produkt-evaluering, må ha de samme dimensjonene, noe som antyder at du kan bruke Summer produkt med to rader eller to kolonner, men ikke med én kolonne og én rad.
Som et eksempel på hvordan vi kan bruke Summer produkt-funksjonen i produkt sammensetnings eksempelet, kan vi beregne ressurs bruken vår. Bruken av arbeids kraft beregnes av
(Arbeids kraft som brukes per pund av legemiddel 1) * (pund produsert i legemiddel 1) +
(arbeid brukt per pund av legemiddel 2) * (pund produsert av legemiddel 2) +...
(Arbeids kraft som brukes per pund av legemiddel 6) * (pund produsert av legemiddel 6)
Vi kan beregne bruk av arbeid på en mer kjedelig måte som D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + i2 * I4. På samme måte kunne rå Material bruk beregnes som D2 * D5 + E2 *E5 + F2 * F5 + G2 * G5 + H2 * H5 + i2 * i5. Det er imidlertid tid krevende å skrive inn disse formlene i et regne ark for seks produkter. Tenk over hvor lang tid det ville ha hvis du arbeidet med et selskap som produseres, for eksempel 50-produkter i planten. En mye enklere måte å beregne arbeids kraft og rå vare bruk på, er å kopiere fra D14 til D15 formelen Summer produkt ($D $2: $I $2, D4: i4). Denne formelen beregner D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + i2 * I4 (som er vår bruk av arbeids kraft), men er mye enklere å angi! Legg merke til at jeg bruker $-tegnet med Range D2: I2, slik at når jeg kopierer formelen, tar du fortsatt opp produkt sammensetningen fra rad 2. Formelen i celle D15 beregner bruk av rå varer.
På samme måte avhenger vår fortjeneste av
(Fortjeneste per pund for legemiddel 1) * (pund produsert i legemiddel 1) +
(fortjeneste på legemiddel 2 per pund) * (pund produsert av legemiddel 2) +...
(Fortjeneste per pund for legemiddel 6) * (pund produsert av legemiddel 6)
ForTjenesten beregnes enkelt i celle D12 med formelen Summer produkt (D9: i9, $D $2: $I $2).
Vi kan nå identifisere de tre komponentene i produkt sammensetnings modellen.
-
Mål celle.Målet vårt er å gi størst mulig fortjeneste (beregnet i celle D12).
-
Endring av celler.Antall pund som produseres av hvert produkt (oppført i celle området D2: I2)
-
Begrensninger. Vi har følgende betingelser:
-
Ikke bruk mer arbeids kraft eller RAW-materiale enn det som er tilgjengelig. Det vil si at verdiene i cellene D14: D15 (ressursene som brukes) må være mindre enn eller lik verdiene i cellene F14: F15 (de tilgjengelige ressursene).
-
Ikke produsere mer av et legemiddel enn det er behov for. Det vil si at verdiene i cellene D2: I2 (pund produsert av hvert legemiddel) må være mindre enn eller lik etterspørselen etter hvert legemiddel (oppført i celle D8: I8).
-
Vi kan ikke produsere et negativt beløp for et legemiddel.
-
Jeg viser deg hvordan du skriver inn mål cellen, endrings cellene og begrensningene i problem løseren. Alt du trenger å gjøre, er å klikke løs-knappen for å finne en produkt sammensetning som er maksimert.
Hvis du vil begynne, klikker du data-fanen, og i analyse-gruppen klikker du problem løser.
Obs!: Som forklart i kapittel 26 kan du "en innføring i optimalisering med Excel problem løser," problem løseren er installert ved å klikke Microsoft Office-knappen, alternativer for Excel, etterfulgt av tillegg. Klikk Excel-tillegg i behandle-listen, Merk av for problem Løserens tillegg, og klikk deretter OK.
Dialog boksen problem løser parametere vises, som vist i figur 27-2.
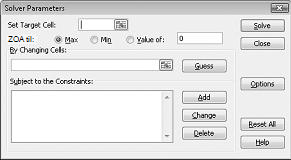
Klikk i boksen Angi mål celle, og velg deretter fortjeneste-cellen (celle D12). Klikk boksen ved endring av celler, og pek deretter på området D2: I2, som inneholder pund produsert av hvert legemiddel. Dialog boksen skal nå se ut figur 27-3.
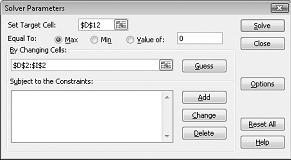
Vi er nå klar til å legge til betingelser i modellen. Klikk på Legg til-knappen. Du vil se dialog boksen Legg til begrensning, som vises i figur 27-4.
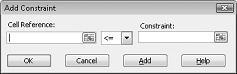
Hvis du vil legge til begrensningene for ressurs bruk, klikker du boksen celle referanse, og deretter merker du området D14: D15. Velg < = fra den midterste listen. Klikk betingelse-boksen, og merk deretter celle området F14: F15. Dialog boksen Legg til begrensning skal nå se ut som figur 27-5.
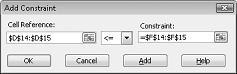
Vi har nå sikret at når problem løser prøver forskjellige verdier for endrings cellene, er det bare kombinasjoner som oppfyller både D14< = F14 (arbeid som brukes er mindre enn eller lik tilgjengelig arbeid) og D15< = F15 (rå varer som brukes er mindre enn eller lik tilgjengelig rå Material) vil bli vurdert. Klikk Legg til for å angi begrensningene for etterspørsel. Fyll ut dialog boksen Legg til begrensning som vist i figur 27-6.
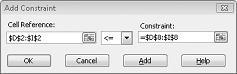
Hvis du legger til disse betingelsene, sikrer du at når problem løser prøver ulike kombinasjoner for endrings celle verdiene, blir bare kombinasjoner som oppfyller følgende parametere, vurdert:
-
D2< = D8 (beløpet produsert av legemiddel 1 er mindre enn eller lik etterspørselen etter legemiddel 1)
-
E2< = E8 (mengden produsert av legemiddel 2 er mindre enn eller lik etterspørselen etter legemiddel 2)
-
F2< = F8 (beløpet produsert av legemiddel 3 som er gjort mindre enn eller lik etterspørselen etter legemiddel 3)
-
G2< = G8 (beløpet produsert av legemiddel 4 som er gjort mindre enn eller lik etterspørselen etter legemiddel 4)
-
H2< = H8 (beløpet produsert av legemiddel 5 er mindre enn eller lik etterspørselen etter legemiddel 5)
-
I2< = I8 (beløpet produsert av legemiddel 6 som er gjort mindre enn eller lik etterspørselen etter legemiddel 6)
Klikk OK i dialog boksen Legg til begrensning. Problem løser vinduet skal se ut som figur 27-7.
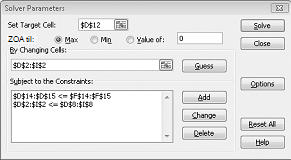
Vi skriver inn Begrensningen som endrer celler må være ikke-negative i dialog boksen alternativer for problem løser. Klikk Alternativer-knappen i dialog boksen problem løser parametere. Merk av for Anta lineær modell og anta ikke-negativ-boksen, som vist i figur 27-8 på neste side. Klikk OK.
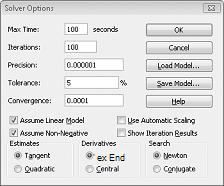
Hvis du merker av for anta ikke-negativ-boksen, sikrer problem løser bare kombinasjoner av endrings celler der hver endrings celle antar en ikke-negativ verdi. Vi sjekket ut boksen Anta lineær modell fordi produkt sammensetnings problemet er en spesiell type problem løser problem som kalles en lineær modell. I hoved sak er en problem løser modell lineær under følgende betingelser:
-
Mål cellen beregnes ved å legge sammen termene for skjemaet (endrings celle) * (konstant).
-
Hver betingelse oppfyller kravet til lineær modell. Dette betyr at hver betingelse evalueres ved å legge sammen termene for skjemaet (endrings celle) * (konstant) og sammenligne summene med en konstant.
Hvorfor er dette problem løser problemet lineært? Mål cellen (fortjenesten) beregnes som
(Fortjeneste per pund for legemiddel 1) * (pund produsert i legemiddel 1) +
(fortjeneste på legemiddel 2 per pund) * (pund produsert av legemiddel 2) +...
(Fortjeneste per pund for legemiddel 6) * (pund produsert av legemiddel 6)
Denne beregningen følger et mønster der mål cellens verdi er avledet ved å legge sammen termer på skjemaet (endrings celle) * (konstant).
Arbeids betingelsen vår vurderes ved å sammenligne verdien avledet fra (arbeid brukt per pund av legemiddel 1) * (pund produsert av legemiddel 1) + (arbeids kraft per pund av legemiddel 2) * (pund produsert av legemiddel 2) +... (Arbeidernes USEd per pund av legemiddel 6) * (legemiddel 6 pund produsert) til tilgjengelig arbeid.
Derfor vurderes arbeids begrensningen ved å legge sammen vilkårene for skjemaet (endrings celle) * (konstant) og sammenligne summene med en konstant. Både begrensningen for arbeids kraft og rå varer oppfyller kravene til lineær modell.
Etterspørsels betingelsene våre bruker skjemaet
(Produsert legemiddel 1) < = (etterspørsel legemiddel 1)
(produsert legemiddel 2) < = (etterspørsel legemiddel 2)
§
(produsert legemiddel 6) < = (etterspørsel legemiddel 6 )
Hver etterspørsels begrensning oppfyller også kravene til lineær modell, fordi hver av dem vurderes ved å legge sammen vilkårene i skjemaet (endrings celle) * (konstant) og sammenligne summene med en konstant.
Hvis du har vist at produkt sammensetnings modellen er en lineær modell, hvorfor skal vi bry oss om det?
-
Hvis en problem løser modell er lineær og vi velger Anta lineær modell, er problem løseren garantert å finne den optimale løsningen på modellen for problem løser. Hvis en problem løser modell ikke er lineær, kan det hende at problem løser eller ikke finner den optimale løsningen.
-
Hvis en problem løser modell er lineær og vi velger Anta lineær modell, bruker problem løseren en svært effektiv algoritme (simpleks metoden) for å finne modellens optimale løsning. Hvis en problem løser modell er lineær og vi ikke velger Anta lineær modell, bruker problem løseren en svært effektiv algoritme (GRG2-metoden) og kan ha problemer med å finne modellens optimale løsning.
Når du klikker OK i dialog boksen alternativer for problem løser, går vi tilbake til hoveddialogboksen for problem løser, som vises tidligere i figur 27-7. Når vi klikker løs, beregner problem løseren en optimal løsning (hvis det finnes) for produkt sammensetnings modellen. Som jeg har angitt i kapittel 26, ville en optimal løsning på produkt sammensetnings modellen være et sett med endrings celle verdier (pund produsert av hvert legemiddel) som maksimerer fortjenesten over settet av alle mulige løsninger. På nytt er en mulig løsning et sett med endrings celle verdier som oppfyller alle begrensningene. Endrings celle verdiene som vises i figur 27-9, er en mulig løsning fordi alle produksjons nivåene er ikke-negative, produksjons nivåene overskrider ikke etterspørselen, og ressurs bruken overskrider ikke tilgjengelige ressurser.
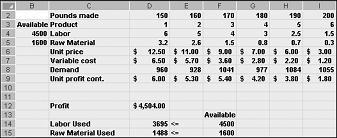
Endrings celle verdiene som vises i figur 27-10 på den neste siden, representerer en umulig løsning av følgende årsaker:
-
Vi gir mer av legemiddel 5 enn etterspørselen etter det.
-
Vi bruker mer arbeid enn det som er tilgjengelig.
-
Vi bruker mer råre materiale enn det som er tilgjengelig.
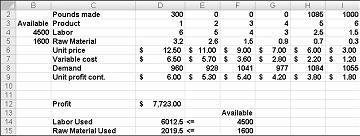
Når du har klikket løs, finner problem løseren den optimale løsningen som vises i figur 27-11. Du må velge Behold problem løser løsningen for å beholde de optimale løsnings verdiene i regne arket.
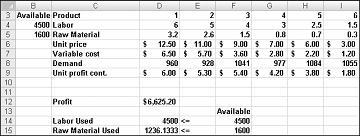
Vårt farmasøytiske firma kan maksimere den månedlige fortjenesten på et nivå på $6 625,20 ved å produsere 596,67 pund av legemiddel 4, 1084 pund av legemiddel 5 og ingen andre stoff! Vi finner ikke ut om vi kan oppnå maksimal fortjeneste på $6 625,20 på andre måter. Alt vi kan være sikker på at du er med våre begrensede ressurser og etterspørsel, er det ikke mulig å gjøre mer enn $6 627,20 denne måneden.
La oss si at etterspørselen etter hvert produkt må oppfylles. (Se ingen mulige løsnings forslag i filen prodmix. xlsx.) Vi må da endre etterspørsels begrensningene fra D2: I2< = D8: I8 til D2: I2> = D8: I8. Hvis du vil gjøre dette, åpner du problem løser, velger D2: I2< = D8: I8-betingelse, og deretter klikker du endre. Dialog boksen Endre begrensning, som vises i figur 27-12, vises.
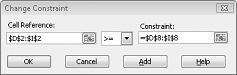
Velg > =, og klikk deretter OK. Vi har nå sikret at problem løseren vurderer å endre bare celle verdier som oppfyller alle kravene. Når du klikker løs, ser du meldingen «problem løseren fant ikke en mulig løsning.» Denne meldingen betyr ikke at vi har gjort en feil i modellen vår, men i stedet kan vi ikke innfri etterspørselen etter alle produkter, men ikke med våre begrensede ressurser. Problem løseren sier at hvis vi vil innfri etterspørselen etter hvert produkt, må vi legge til mer arbeid, mer rå varer eller flere av begge.
La oss se hva som skjer hvis vi tillater ubegrenset etterspørsel for hvert produkt, og vi tillater at negative mengder blir produsert av hvert legemiddel. (Du kan se dette problem løser problemet på Set-verdiene ikke sammenfaller regne arket i filen prodmix. xlsx.) Hvis du vil finne den optimale løsningen for denne situasjonen, åpner du problem løser, klikker Alternativer-knappen og fjerner merket for anta ikke-negativ. I dialog boksen problem løser parametere velger du etterspørsels begrensning D2: I2< = D8: I8 og deretter klikker du Slett for å fjerne betingelsen. Når du klikker på løs, returnerer problem løser meldingen «angi celle verdier sammenfaller ikke». Denne meldingen betyr at hvis mål cellen skal maksimeres (som i eksempelet vårt), finnes det mulige løsninger med vilkårlig store mål celle verdier. (Hvis mål cellen skal minimeres, sammenfaller ikke meldingen «sett celle verdier sammen "betyr at det finnes mulige løsninger med vilkårlig små celle verdier.) I vår situasjon, ved å tillate negativ produksjon av et legemiddel, har vi innvirkning på «Opprett» ressurser som kan brukes til å produsere vilkårlige store mengder andre stoffer. Hvis du har fått ubegrenset etterspørsel, kan vi gjøre ubegrenset fortjeneste. I en virkelig situasjon kan vi ikke lage et ubegrenset antall penger. Hvis du ser «angitt verdier sammenfaller ikke, har ikke modellen en feil.
-
La oss si at vårt farmasøytiske firma kan kjøpe opptil 500 timer med arbeid på $1 ganger per time enn gjeldende arbeids kostnader. Hvordan kan vi maksimere fortjeneste?
-
Fire teknikere (A, B, C og D) gir tre produkter (Products 1, 2 og 3) til en brikke produksjons plante. Denne måneden kan brikke produsenten selge 80 enheter av produkt 1, 50-enheter for produkt 2 og maksimum 50s enheter av produkt 3. Tekniker A kan bare gjøre produkt 1 og 3. Tekniker B kan bare gi produkt 1 og 2. Tekniker C kan bare gjøre produkt 3. Tekniker D kan bare gjøre produkt 2. For hver enhet som produseres, bidrar produktene til følgende fortjeneste: produkt 1, $6; Produkt 2, $7; og produkt 3, $10. Tiden (i timer) hver tekniker trenger for å produsere et produkt, er som følger:
Product
Tekniker A
Tekniker B
Tekniker C
Tekniker D
1
2
2,5
Kan ikke gjøre
Kan ikke gjøre
2
Kan ikke gjøre
3
Kan ikke gjøre
3,5
3
3
Kan ikke gjøre
4
Kan ikke gjøre
-
Hver tekniker kan arbeide opptil 120 timer per måned. Hvordan kan brikke produsenten maksimere den månedlige fortjenesten? Anta at en brøk del av antall enheter kan produseres.
-
En data maskin fabrikk produserer mus, tastaturer og video spill styre spaker. Forbruks resultatet per enhet, månedlig etterspørsel og maskin per enhet i tabellen nedenfor, er angitt for arbeids kraft.
Mus
Tastaturer
Styre spaker
Fortjeneste/enhet
$8
$11
$9
Forbruk av arbeids kraft/enhet
.2 timer
.3 time
24 timer
Maskin tid/enhet
.04 time
.055 time
.04 time
Månedlig etterspørsel
15 000
27 000
11 000
-
Hver måned er totalt 13 000 arbeids timer og 3000 timer data maskin tid tilgjengelig. Hvordan kan produsenten maksimere det månedlige fortjeneste bidraget fra planten?
-
Løs legemiddel eksempelet vårt anta at et minimums behov på 200-enheter for hvert legemiddel må oppfylles.
-
Jason gjør Diamond Bracelets, necklaces og earrings. Han ønsker å arbeide maksimalt 160 timer per måned. Han har 800 ounce av ruter. Fortjeneste, arbeids tid og ounce av ruter som kreves for å produsere hvert produkt, er angitt nedenfor. Hvis etterspørselen etter hvert produkt er ubegrenset, hvordan kan Jason maksimere fortjenesten?
Product
Enhets fortjeneste
Arbeids timer per enhet
Ounce av ruter per enhet
Bracelet
kr 300
.35
1.2
Necklace
kr 200
.15
.75
Earrings
$100
,05
5










