Korzystanie z do narzędzia Solver do budżetowania kapitału

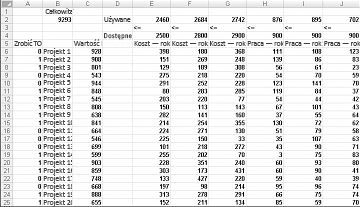
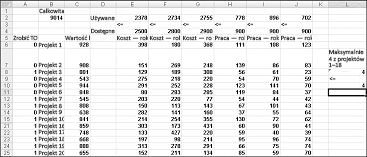
Większość firm chce podejmować projekty, które przysyłają wartość bieżącą netto (NPV) przy ograniczonych zasobach (zazwyczaj jest to kapitał i kapitał). Załóżmy, że firma deweloperska próbuje ustalić, który z 20 projektów oprogramowania powinien podjąć. Wartość NPV (w milionach złotych) spłacana przez każdy projekt, jak również kapitał (w milionach złotych) oraz liczba programistów potrzebnych w ciągu kolejnych trzech lat jest podana w arkuszu Model podstawowy w pliku Capbudget.xlsx, który przedstawiono na rysunku 30-1 na następnej stronie. Na przykład Project 2 zł daje 908 milionów zł. Wymaga ona 151 milionów USD w roku 1, 269 milionów USD w roku 2 i 248 milionów USD w roku 3. Project 2 wymaga 139 programistów w roku 1, 86 programistów w roku 2, a 83 programistów w roku 3. Komórki E4:G4 pokazują kapitał (w milionach złotych) dostępny w każdym z trzech lat, a komórki H4:J4 wskazują, ilu programistów jest dostępnych. Na przykład w roku 1 roku dostępnych jest do 2,5 miliarda usd kapitału i 900 programistów.

Firma musi podjąć decyzję, czy podjąć decyzje w sprawie każdego projektu. Załóżmy, że nie możemy podejmować części projektu oprogramowania. Jeśli na przykład przydzielimy 0,5 potrzebnego zasobów, będziemy mieć program dla osób niebędących współpracownikami, który przyniosłby nam przychód w wysokości 0 ZŁ!

W przypadku modelowania sytuacji, w których albo robisz coś, albo tego nie robisz, jest użycie binarnych zmian komórek. Komórka zmieniana w postaci binarnej zawsze jest równa 0 lub 1. Gdy binarna komórka zmieniająca się odpowiadająca projektowi jest równa 1, to robisz projekt. Jeśli binarna komórka, która odpowiada projektowi, jest równa 0, nie zrobimy tego projektu. Dodatek Solver jest tak ustawiony, aby zmieniał zakres binarnych komórek przez dodanie ograniczenia — zaznacz komórki, których chcesz użyć, a następnie wybierz z listy pozycję Przedział w oknie dialogowym Dodawanie ograniczenia.

W tym tle możesz już rozwiązać problem z wyborem projektu oprogramowania. Tak jak w przypadku modelu do rozwiązywania, zaczynamy od zidentyfikowania komórki docelowej, komórek zmieniających się i ograniczeń.

• Komórka docelowa. Maksymalizuje wartość NPV wygenerowaną przez wybrane projekty.

• Zmienianie komórek. Czekamy na 0 lub 1 binarną komórkę zmienianą dla każdego projektu. Komórki te znajdują się w zakresie A6:A25 (i mają nazwę doit zakresu). Na przykład komórka A6 1 wskazuje, że podejmujemy się Project 1, a 0 w komórce C6 wskazuje, że nie podejmujemy się Project 1.

• Ograniczenia. Musimy zapewnić, że dla każdego Roku t (t=1, 2, 3), Używanego roku kapitaliki jest mniejsze lub równe Dostępnemu rokowi, a używany ilość pracy t jest mniejsza lub równa dostępnemu pracy w roku.

Jak widać, nasz arkusz musi zostać obliczony dla dowolnego wyboru projektów NPV, capital używanego co rok, a programiści używali każdego roku. W komórce B2 używam formuły SUMA.IPRODUKTÓW(doit;NPV) do obliczenia całkowitej wartości NPV wygenerowanej przez wybrane projekty. (Nazwa zakresu NPV odwołuje się do zakresu C6:C25). W przypadku każdego projektu z wartością 1 w kolumnie A formuła odbiera wartość NPV projektu, a w przypadku każdego projektu z wartością 0 w kolumnie A formuła nie wybiera wartości NPV projektu. Dlatego można obliczyć NPV wszystkich projektów, a nasza komórka docelowa jest liniowa, ponieważ jest obliczana przez sumowanie terminów, które są zgodne z formularzem (zmiana komórki )*(stała). Podobnie obliczam używaną w roku kapitaliki i użytą w roku pracę, kopiując z E2 do F2:J2 formułę SUMA.IPRODUKTU (doit;E6:E25).

Teraz wypełniam okno dialogowe Parametry dopełniacza, jak pokazano na rysunku 30–2.

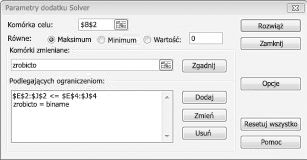
Naszym celem jest zmaksymalizowanie wartości NPV wybranych projektów (komórka B2). Nasze zmieniane komórki (zakres o nazwie doit) to binarne komórki zmieniane w poszczególnych projektach. Ograniczenie E2:J2<=E4:J4 gwarantuje, że w ciągu każdego roku używany kapitał i rynku pracy będą mniejsze lub równe dostępnemu kapitalowi i rynku pracy. Aby dodać ograniczenie, dzięki czemu zmieniane komórki jako binarne, klikam przycisk Dodaj w oknie dialogowym Parametry dodatku Solver, a następnie wybieram pozycję Bin z listy w środku okna dialogowego. Okno dialogowe Dodawanie ograniczenia powinno zostać wyświetlone na rysunku 30-3.

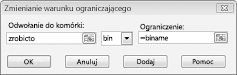
Nasz model jest liniowy, ponieważ komórka docelowa jest obliczana jako suma terminów, które mają postać (zmieniając komórkę )*(stała) i ponieważ ograniczenia użycia zasobów są obliczane przez porównanie sumy (zmienianie komórek )*(stałych) ze stałą.

Po wypełnieniu okna dialogowego Parametry dopełniacza kliknij przycisk Rozwiąż, a wyniki zostaną wyświetlone wcześniej na rysunku 30-1. Firma może uzyskać maksymalną wartość NPV w wysokości 9 293 milionów USD (9,293 miliona USD) poprzez wybranie projektów 2, 3, 6–10, 14–16, 19 i 20.

Czasami modele wyboru projektu mają inne ograniczenia. Załóżmy na przykład, że jeśli wybierzemy pozycję Project 3, należy również wybrać pozycję Project 4. Ponieważ nasze bieżące optymalne rozwiązanie wybiera numer Project 3, ale nie Project 4, wiemy, że nasze bieżące rozwiązanie nie może pozostać optymalne. Aby rozwiązać ten problem, po prostu dodaj ograniczenie, że zmiana binarna komórki dla liczby Project 3 jest mniejsza niż lub równa zmieniana komórka binarna dla liczby Project 4.

Ten przykład można znaleźć na arkuszu Jeżeli 3, a potem 4 w Capbudget.xlsx, co przedstawiono na rysunku 30-4. Komórka L9 odwołuje się do wartości binarnej powiązanej z Project 3, a komórka L12 do wartości binarnej powiązanej z Project 4. Dodając ograniczenie L9<=L12, jeśli wybierzemy wartość Project 3, L9 będzie równe 1, a nasze siły ograniczenia L12 (Project postaci binarnej 4) równe 1. Nasze ograniczenie musi również pozostawić wartość binarną w zmienianej komórce komórki Project 4 nieograniczone, jeśli nie wybierzemy liczby Project 3. Jeśli nie wybierzemy wartości Project 3, L9 będzie równe 0, Project ograniczenie umożliwi wartości binarnej Project 4 równe 0 lub 1, co jest tym, czego chcemy. Nowe optymalne rozwiązanie pokazano na rysunku 30-4.

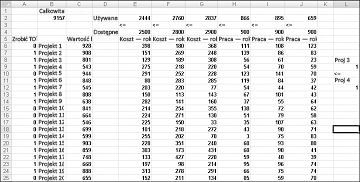
Nowe optymalne rozwiązanie jest obliczane, jeśli Project 3 oznacza, że należy również wybrać pozycję Project 4. Teraz można wykonać tylko cztery projekty w ramach projektów od 1 do 10. (Zobacz arkusz Co najwyżej 4 z P1–P10 , pokazany na rysunku 30-5). W komórce L8 obliczamy sumę wartości binarnych skojarzonych z projektami od 1 do 10 za pomocą formuły SUMA(A6:A15). Następnie dodajemy ograniczenie L8<=L10, co zapewnia, że zaznaczono co najwyżej 4 z pierwszych 10 projektów. Nowe optymalne rozwiązanie pokazano na rysunku 30-5. Wartość npv została upuszczona do 9,014 usd.

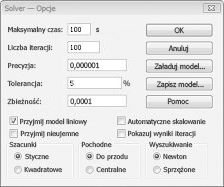
Modele liniowe do rozwiązywania problemów, w których niektóre lub wszystkie zmieniające się komórki są wymagane do postaci binarnej lub całkowitej, są zazwyczaj trudniejsze do rozwiązania niż modele liniowe, w których wszystkie zmieniane komórki mogą być ułamkami. Z tego powodu często jesteśmy zadowoleni z niemal optymalnego rozwiązania problemu z kodami liczb całkowitych lub binarnych. Jeśli model do rozwiązywania działa przez długi czas, warto rozważyć dostosowanie ustawienia Marginesy w oknie dialogowym Opcje do solver. (Zobacz rysunek 30-6). Na przykład ustawienie Tolerancja dla wartości 0,5% oznacza, że narzędzie Solver zatrzyma się po raz pierwszy, gdy znajdzie rozwiązanie możliwe do znalezienie w zakresie 0,5 procenta optymalnej wartości komórki docelowej. Często mamy do czynienia z wyborem między znalezieniem odpowiedzi w ciągu 10 procent od optymalnej w ciągu 10 minut lub znalezieniem optymalnego rozwiązania w ciągu dwóch tygodni pracy komputera! Domyślna wartość tolerancji to 0,05%, co oznacza, że narzędzie Solver zatrzymuje się po znalezienie wartości komórki docelowej z dokładnością do 0,05 procenta optymalnej wartości komórki docelowej.

1. W firmie jest rozważanych dziewięć projektów. W poniższej tabeli przedstawiono wartość NPV dodaną w każdym projekcie oraz wartość capital wymaganą w każdym projekcie w kolejnych dwóch latach. (Wszystkie liczby są w milionach). Na przykład wartość Project 1 spowoduje dodanie 14 milionów zł w npv i wymaga wydatków w wysokości 12 milionów zł w roku 1 i 3 milionów zł w roku 2. W roku 1 dostępny jest 50 milionów usd kapitału w projektach, a w roku 2 jest dostępny 20 milionów usd.

	NPV	Wydatki w roku 1	Wydatki w roku 2
Project 1	14	12	3
Project 2	17	54	7
Project 3	17	6	6
Project 4	15	6	2
Project 5	40	30	35
Project 6	12	6	6
Project 7	14	48	4
Project 8	10	36	3
Project 9	12	18	3

• Jeśli nie jesteśmy w stanie podejmować części projektu, ale muszą podejmować działania w ramach całego projektu lub żadnego z jego projektów, jak możemy zmaksymalizować npv?

• Załóżmy, że Project 4 zostanie podjęte, należy Project 5. Jak możemy zmaksymalizować npv?

• Publikująca firma próbuje ustalić, którą z 36 książek ma opublikować w tym roku. Plik, Pressdata.xlsx zawiera następujące informacje na temat każdej książki:

  • Prognozowane koszty przychodów i rozwoju (w tysiącach złotych)

  • Strony w każdej książce

  • Czy książka jest przekierowyowana do grupy odbiorców oprogramowania (wskazywana przez 1 w kolumnie E)

    Publikująca firma może w tym roku publikować książki o sumie 8500 stron i publikować co najmniej cztery książki dla deweloperów oprogramowania. Jak firma może zmaksymalizować swój zysk?

Ten artykuł został zaadaptowany z Microsoft Office Excel 2007 r. i modelowania biznesowego przez Wayne'a L. Winstona.

Ta książka klasowa została opracowana na podstawie serii prezentacji autorstwa Wayne'a Winstona, znanego specjalisty i wykładowcy biznesowego, który koncentruje się w kreatywnych, praktycznych zastosowaniach Excel.