Ważne: Wsparcie techniczne dla pakietów Office 2016 i Office 2019 zakończyło się 14 października 2025 r.. Uaktualnij do platformy Microsoft 365, aby pracować w dowolnym miejscu, z dowolnego urządzenia i nadal uzyskiwać pomoc techniczną. Pobierz platformę Microsoft 365
W tym artykule omówiono korzystanie z dodatku Solver do programu Microsoft Excel, który umożliwia analizę warunkową w celu określenia optymalnej kombinacji produktów.
Jak ustalić miesięczny zestaw produktów, który maksymalizuje rentowność?
Firmy często muszą określić ilość każdego produktu do produkcji w ujęciu miesięcznym. W najprostszej formie problem z mieszanką produktów polega na tym, jak określić ilość każdego produktu, który powinien być wyprodukowany w ciągu miesiąca, aby zmaksymalizować zyski. Kombinacja produktów musi zazwyczaj stosować się do następujących ograniczeń:
-
W przypadku miksu produktów nie można użyć większej liczby zasobów, niż jest dostępnych.
-
Istnieje ograniczone zapotrzebowanie na każdy produkt. Nie możemy produkować więcej produktu w ciągu miesiąca, niż nakazuje popyt, ponieważ nadmiar produkcji jest marnowany (na przykład, psująca się lek).
Teraz rozwiążmy poniższy przykład problemu z miksem produktów. Rozwiązanie tego problemu można znaleźć w Prodmix.xlsx pliku, pokazanym na ilustracji 27-1.
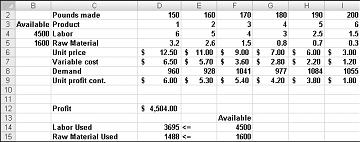
Załóżmy, że pracujemy dla firmy farmaceutycznej, która produkuje sześć różnych produktów w ich zakładzie. Produkcja każdego produktu wymaga pracy i surowca. Wiersz 4 na rysunku 27-1 pokazuje godziny pracy potrzebnej do produkcji funta każdego produktu, a wiersz 5 pokazuje funty surowców potrzebnych do produkcji funta każdego produktu. Na przykład produkcja funta produktu 1 wymaga sześciu godzin pracy i 3,2 funta surowca. Dla każdego leku cena za funt jest podana w wierszu 6, koszt jednostkowy za funt jest podawany w wierszu 7, a wkład zysku na funta jest podawany w wierszu 9. Na przykład produkt 2 sprzedaje się za 11,00 usd za funt, ponosi koszt jednostkowy w wysokości 5,70 USD za funt i przyczynia się do 5,30 USD zysku za funt. Miesięczne zapotrzebowanie na każdy lek jest podawane w wierszu 8. Na przykład, popyt na produkt 3 wynosi 1041 funtów. W tym miesiącu, 4500 godzin pracy i 1600 funtów surowca są dostępne. Jak ta firma może zmaksymalizować miesięczny zysk?
Gdybyśmy nic nie wiedzieli o dodatku Solver programu Excel, zaatakowalibyśmy ten problem, konstruując arkusz w celu śledzenia zysków i użycia zasobów skojarzonych z miksem produktów. Następnie korzystalibyśmy z prób i błędów, aby zmienić mieszankę produktów, aby zoptymalizować zysk bez użycia większej siły roboczej lub surowca niż jest dostępna, i bez produkcji żadnego leku przekraczającego popyt. Dodatek Solver jest używany w tym procesie tylko na etapie próby i błędu. Zasadniczo solver jest aparatem optymalizacji, który bezbłędnie wykonuje wyszukiwanie prób i błędów.
Kluczem do rozwiązania problemu z miksem produktów jest efektywne obliczanie użycia zasobów i zysków związanych z daną kombinacją produktów. Ważnym narzędziem, za pomocą którego możemy wykonać tę obliczenia, jest funkcja SUMA.ILOCZYNÓW. Funkcja SUMA.ILOCZYNÓW mnoży odpowiadające im wartości w zakresach komórek i zwraca sumę tych wartości. Każdy zakres komórek używany w obliczeniach SUMA.ILOCZYNÓW musi mieć takie same wymiary, co oznacza, że można używać SUMA.ILOCZYNÓW z dwoma wierszami lub dwiema kolumnami, ale nie z jedną kolumną i jednym wierszem.
Jako przykład tego, jak możemy użyć funkcji SUMA.ILOCZYNÓW w naszym przykładzie mieszanki produktów, spróbujmy obliczyć użycie naszych zasobów. Nasze wykorzystanie pracy jest obliczane przez
(Praca stosowana na funt leku 1)*(Lek 1 funt wyprodukowany)+ (Labor używane na funt leku 2)*(Lek 2 funtów wyprodukowane) + ... (Labor używane na funt leku 6)*(Lek 6 funtów wyprodukowane)
Możemy obliczyć użycie pracy w bardziej żmudny sposób, jak D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Podobnie użycie surowców można obliczyć jako D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Jednak wprowadzenie tych formuł w arkuszu dla sześciu produktów jest czasochłonne. Wyobraź sobie, jak długo to potrwa, jeśli pracujesz z firmą, która wyprodukowała na przykład 50 produktów w ich zakładzie. Znacznie łatwiejszym sposobem obliczania zużycia pracy i surowców jest skopiowanie z D14 do D15 formuły SUMA.ILOCZYNÓW($D$2:$I$2;D4:I4). Ta formuła oblicza D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (co jest naszym obciążeniem pracy), ale jest znacznie łatwiejsze do wprowadzania! Zwróć uwagę, że używam znaku $ z zakresem D2:I2, aby podczas kopiowania formuły nadal przechwytywać mieszankę produktów z wiersza 2. Formuła w komórce D15 oblicza użycie surowca.
W podobny sposób nasz zysk jest określany przez
(Drug 1 zysk na funt)*(Lek 1 funt wyprodukowany) + (Drug 2 zysk na funt)*(Drug 2 funtów wyprodukowane) + ... (Drug 6 zysk na funt)*(Lek 6 funtów wyprodukowane)
Zysk można łatwo obliczyć w komórce D12 za pomocą formuły SUMA.ILOCZYNÓW(D9:I9;$D$2:$I$2).
Teraz możemy zidentyfikować trzy składniki naszego modelu dodatku Solver dla miksu produktów.
-
Komórka docelowa. Naszym celem jest zmaksymalizowanie zysku (obliczonego w komórce D12).
-
Zmienianie komórek. Liczba funtów wyprodukowanych z każdego produktu (wymienione w zakresie komórek D2:I2)
-
Ograniczenia. Mamy następujące ograniczenia:
-
Nie stosuj większej siły roboczej ani surowców niż jest to dostępne. Oznacza to, że wartości w komórkach D14:D15 (używane zasoby) muszą być mniejsze lub równe wartościom w komórkach F14:F15 (dostępne zasoby).
-
Nie wytwarzaj więcej leku niż jest popyt. Oznacza to, że wartości w komórkach D2:I2 (funtów wyprodukowanych z każdego leku) musi być mniejsza lub równa zapotrzebowaniu na każdy lek (wymienione w komórkach D8:I8).
-
Nie możemy produkować ujemnej ilości żadnego leku.
-
Pokażę, jak wprowadzić komórkę docelową, zmienić komórki i ograniczenia w dodatku Solver. Następnie wszystko, co musisz zrobić, to kliknąć przycisk Rozwiąż, aby znaleźć zysk maksymalizacji mix produktów!
Aby rozpocząć, kliknij kartę Dane, a następnie w grupie Analiza kliknij pozycję Solver.
Uwaga: Jak wyjaśniono w rozdziale 26 "Wprowadzenie do optymalizacji za pomocą dodatku Excel Solver", dodatek Solver jest instalowany, klikając przycisk pakietu Microsoft Office, a następnie pozycję Opcje programu Excel, a następnie pozycję Dodatki. Na liście Zarządzaj kliknij pozycję Dodatki programu Excel, zaznacz pole dodatku Solver, a następnie kliknij przycisk OK.
Zostanie wyświetlone okno dialogowe Parametry dodatku Solver, jak pokazano na ilustracji 27-2.
Kliknij pole Ustaw komórkę docelową, a następnie wybierz komórkę zysku (komórka D12). Kliknij pole Przez zmianę komórek, a następnie wskaż zakres D2:I2, który zawiera funty wyprodukowane z każdego leku. Okno dialogowe powinno teraz wyglądać na rysunek 27-3.
Teraz możemy dodać ograniczenia do modelu. Kliknij przycisk Dodaj. Zostanie wyświetlone okno dialogowe Dodawanie ograniczenia widoczne na rysunku 27–4.
Aby dodać ograniczenia użycia zasobów, kliknij pole Odwołanie do komórki, a następnie wybierz zakres D14:D15. Wybierz pozycję <= na środkowej liście. Kliknij pole Ograniczenie, a następnie zaznacz zakres komórek F14:F15. Okno dialogowe Dodawanie ograniczenia powinno teraz wyglądać jak rysunek 27–5.
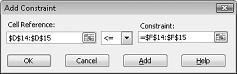
Teraz zapewniliśmy, że podczas próby dodatku Solver różnych wartości dla zmieniających się komórek będą uwzględniane tylko kombinacje spełniające wymagania zarówno D14,<=F14 (używana praca jest mniejsza niż lub równa dostępnej pracy), jak i D15<=F15 (użyty surowiec jest mniejszy lub równy dostępnemu surowcowi). Kliknij pozycję Dodaj, aby wprowadzić ograniczenia wymagań. Wypełnij okno dialogowe Dodawanie ograniczenia, jak pokazano na rysunku 27–6.
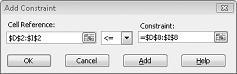
Dodanie tych ograniczeń gwarantuje, że podczas próby dodatku Solver różnych kombinacji dla zmieniających się wartości komórek będą brane pod uwagę tylko kombinacje spełniające następujące parametry:
-
D2<=D8 (ilość wyprodukowanego leku 1 jest mniejsza lub równa zapotrzebowaniu na lek 1)
-
E2<=E8 (ilość wyprodukowanego leku 2 jest mniejsza lub równa zapotrzebowaniu na lek 2)
-
F2<=F8 (ilość wyprodukowanego leku 3 jest mniejsza lub równa zapotrzebowaniu na lek 3)
-
G2<=G8 (ilość wyprodukowanego leku 4 jest mniejsza lub równa zapotrzebowaniu na lek 4)
-
H2<=H8 (ilość wyprodukowanego leku 5 jest mniejsza lub równa zapotrzebowaniu na lek 5)
-
I2<=I8 (ilość wyprodukowanego leku 6 jest mniejsza lub równa zapotrzebowaniu na lek 6)
Kliknij przycisk OK w oknie dialogowym Dodawanie ograniczenia. Okno dodatku Solver powinno wyglądać jak rysunek 27-7.
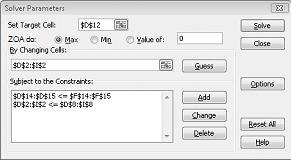
Wprowadzamy ograniczenie, że zmiana komórek musi być nieujemna w oknie dialogowym Opcje dodatku Solver. Kliknij przycisk Opcje w oknie dialogowym Parametry dodatku Solver. Zaznacz pola Załóż model liniowy i Załóżmy, że nie ujemne, jak pokazano na ilustracji 27-8 na następnej stronie. Kliknij przycisk OK.
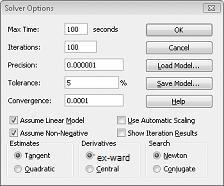
Zaznaczenie pola Załóż, że wartość nie ujemna powoduje, że dodatek Solver uwzględnia tylko kombinacje komórek zmieniających się, w których każda zmieniana komórka przyjmuje wartość nieujemną. Zaznaczyliśmy pole załóżmy, że model liniowy jest problemem z mieszaniem produktów, ponieważ jest to szczególny typ problemu z solverem nazywany modelem liniowym. Zasadniczo model dodatku Solver jest liniowy w następujących warunkach:
-
Komórka docelowa jest obliczana przez połączenie terminów formularza (komórka zmieniająca)*(stała)..
-
Każde ograniczenie spełnia "wymaganie modelu liniowego". Oznacza to, że każde ograniczenie jest obliczane przez dodanie terminów formularza (zmiana komórki)*(stała) i porównanie sum ze stałą.
Dlaczego ten problem z solverem jest liniowy? Nasza komórka docelowa (zysk) jest obliczana jako
(Drug 1 zysk na funt)*(Lek 1 funt wyprodukowany) + (Drug 2 zysk na funt)*(Drug 2 funtów wyprodukowane) + ... (Drug 6 zysk na funt)*(Lek 6 funtów wyprodukowane)
Ta obliczenia są zgodne ze wzorcem, w którym wartość komórki docelowej jest pochodną przez dodanie razem terminów formularza (zmiana komórki)*(stała)..
Nasze ograniczenie pracy jest oceniane przez porównanie wartości pochodzącej z (Labor używane na funt narkotyków 1)*(Drug 1 funtów wyprodukowanych) + (Labor używane na funt narkotyków 2)*(Lek 2 funtów wyprodukowane)+ ... (Popracuj z namied za funt narkotyków 6)*(Lek 6 funtów produkowane) do pracy dostępne.
W związku z tym ograniczenie pracy jest obliczane przez dodanie razem terminów formularza (zmiana komórki)*(stała) i porównanie sum ze stałą. Zarówno ograniczenie pracy, jak i ograniczenie surowca spełniają wymaganie modelu liniowego.
Nasze ograniczenia wymagań przyjmują formę
(Lek 1 wyprodukowany)<=(Lek 1 Popyt) (Lek 2 wyprodukowany)<=(Lek 2 Popyt) §(Lek 6 wyprodukowany)<=(Popyt na lek 6)
Każde ograniczenie zapotrzebowania spełnia również wymaganie modelu liniowego, ponieważ każde z nich jest obliczane przez połączenie terminów formularza (zmiana komórki)*(stała) i porównanie sum ze stałą.
Po pokazaniu, że nasz model mieszanki produktów jest modelem liniowym, dlaczego powinniśmy się tym przejmować?
-
Jeśli model dodatku Solver jest liniowy i wybieramy opcję Załóżmy, że dodatek Solver ma gwarancję znalezienia optymalnego rozwiązania dla modelu dodatku Solver. Jeśli model dodatku Solver nie jest liniowy, dodatek Solver może, ale nie, znaleźć optymalne rozwiązanie.
-
Jeśli model dodatku Solver jest liniowy i wybierzemy opcję Załóżmy, że model liniowy jest używany przez dodatek Solver, w celu znalezienia optymalnego rozwiązania modelu jest używany bardzo wydajny algorytm (metoda simplex). Jeśli model dodatku Solver jest liniowy i nie wybieramy opcji Załóżmy, że dodatek Solver używa bardzo nieefektywnego algorytmu (metody GRG2) i może mieć trudności ze znalezieniem optymalnego rozwiązania modelu.
Po kliknięciu przycisku OK w oknie dialogowym Opcje dodatku Solver wracamy do głównego okna dialogowego dodatku Solver, pokazanego wcześniej na rysunku 27–7. Po kliknięciu przycisku Rozwiąż dodatek Solver oblicza optymalne rozwiązanie (jeśli istnieje) dla naszego modelu miksu produktów. Jak stwierdziłem w rozdziale 26, optymalnym rozwiązaniem dla modelu miksu produktów byłby zestaw zmieniających się wartości komórek (funtów wyprodukowanych z każdego leku), który maksymalizuje zysk w stosunku do zestawu wszystkich możliwych rozwiązań. Rozwiązaniem wykonalnym jest zestaw zmieniających się wartości komórek spełniających wszystkie ograniczenia. Zmieniające się wartości komórek przedstawione na rysunku 27–9 są rozwiązaniem wykonalnym, ponieważ wszystkie poziomy produkcji nie są ujemne, poziomy produkcji nie przekraczają popytu, a użycie zasobów nie przekracza dostępnych zasobów.
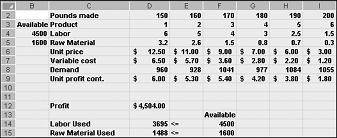
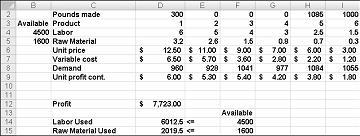
Zmieniające się wartości komórek przedstawione na ilustracji 27–10 na następnej stronie reprezentują możliwe do wyoowania rozwiązanie z następujących powodów:
-
Produkujemy więcej leku 5 niż popyt na niego.
-
Zużywamy więcej pracy niż to, co jest dostępne.
-
Używamy więcej surowców niż jest to, co jest dostępne.
Po kliknięciu przycisku Rozwiąż dodatek Solver szybko znajdzie optymalne rozwiązanie pokazane na rysunku 27–11. Aby zachować optymalne wartości rozwiązań w arkuszu, należy wybrać pozycję Zachowaj rozwiązanie dodatku Solver.
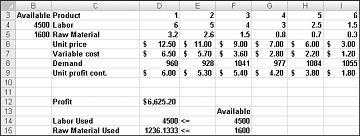
Nasza firma farmaceutyczna może zmaksymalizować swój miesięczny zysk na poziomie $6,625.20 produkując 596.67 funtów Drug 4, 1084 funtów Narkotyków 5, i żaden z innych leków! Nie możemy ustalić, czy możemy osiągnąć maksymalny zysk w wysokości 6625,20 USD w inny sposób. Jedyne, co możemy być pewni, to to, że dzięki naszym ograniczonym zasobom i popytowi nie ma sposobu, aby zarobić więcej niż $6,627.20 w tym miesiącu.
Załóżmy, że wymagania dotyczące każdego produktu muszą zostać spełnione. (Zobacz arkusz Brak możliwości rozwiązania w Prodmix.xlsx pliku). Następnie musimy zmienić ograniczenia popytu z D2:I2<=D8:I8 na D2:I2>=D8:I8. W tym celu otwórz dodatek Solver, wybierz<D2:I2 =D8:I8, a następnie kliknij pozycję Zmień. Zostanie wyświetlone okno dialogowe Zmienianie ograniczenia wyświetlane na rysunku 27–12.
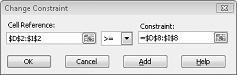
Wybierz pozycję >=, a następnie kliknij przycisk OK. Teraz dodatek Solver rozważy zmianę tylko wartości komórek spełniających wszystkie wymagania. Po kliknięciu przycisku Rozwiąż zostanie wyświetlony komunikat "Dodatek Solver nie może znaleźć możliwego rozwiązania". Ten komunikat nie oznacza, że popełniliśmy błąd w naszym modelu, ale raczej, że przy naszych ograniczonych zasobach nie możemy zaspokoić popytu na wszystkie produkty. Solver po prostu mówi nam, że jeśli chcemy zaspokoić popyt na każdy produkt, musimy dodać więcej pracy, więcej surowców lub więcej obu.
Zobaczmy, co się stanie, jeśli pozwolimy na nieograniczone zapotrzebowanie na każdy produkt i pozwolimy na produkcję ujemnych ilości każdego leku. (Ten problem z dodatkiem Solver jest widoczny w arkuszu Ustaw wartości niekonwergentne w Prodmix.xlsx pliku). Aby znaleźć optymalne rozwiązanie dla tej sytuacji, otwórz dodatek Solver, kliknij przycisk Opcje i wyczyść pole wyboru Załóż, że nie ujemne. W oknie dialogowym Parametry dodatku Solver wybierz ograniczenie demand D2:I2<=D8:I8, a następnie kliknij pozycję Usuń, aby usunąć ograniczenie. Po kliknięciu przycisku Rozwiąż dodatek Solver zwraca komunikat "Ustaw wartości komórek nie są zbieżne". Ten komunikat oznacza, że jeśli komórka docelowa ma zostać zmaksymalizowana (jak w naszym przykładzie), istnieją rozwiązania z dowolnie dużymi wartościami komórek docelowych. (Jeśli komórka docelowa ma zostać zminimalizowana, komunikat "Ustaw wartości komórek nie są zbieżne" oznacza, że istnieją możliwe rozwiązania z dowolnie małymi wartościami komórek docelowych). W naszej sytuacji, zezwalając na negatywną produkcję leku, w efekcie "tworzymy" zasoby, które mogą być wykorzystane do produkcji dowolnie dużych ilości innych leków. Biorąc pod uwagę nasz nieograniczony popyt, pozwala nam to osiągać nieograniczone zyski. W realnej sytuacji nie możemy zarobić nieskończonej kwoty pieniędzy. Krótko mówiąc, jeśli zostanie wyświetlony komunikat "Ustaw wartości niekonwergentne", w modelu jest wyświetlany błąd.
-
Załóżmy, że nasza firma farmaceutyczna może kupić do 500 godzin pracy po 1 USD więcej za godzinę niż obecne koszty pracy. Jak możemy zmaksymalizować zysk?
-
W fabryce chipów czterech techników (A, B, C i D) produkuje trzy produkty (Produkty 1, 2 i 3). W tym miesiącu producent mikroukładu może sprzedać 80 jednostek produktu 1, 50 jednostek produktu 2 i co najwyżej 50 jednostek produktu 3. Technik A może tworzyć tylko produkty 1 i 3. Technik B może tworzyć tylko produkty 1 i 2. Technik C może utworzyć tylko produkt 3. Technik D może utworzyć tylko produkt 2. Dla każdej wyprodukowanej jednostki, produkty przyczyniają się do następującego zysku: Produkt 1, $6; Produkt 2, $7; i Produkt 3, $10. Czas (w godzinach) potrzebny każdemu technikowi do wytworzenia produktu jest następujący:
Produkt
Technik A
Technik B
Technik C
Technik D
1
2
2,5
Nie można tego zrobić
Nie można tego zrobić
2
Nie można tego zrobić
3
Nie można tego zrobić
3,5
3
3
Nie można tego zrobić
4
Nie można tego zrobić
-
Każdy technik może pracować do 120 godzin miesięcznie. Jak producent mikroukładu może zmaksymalizować miesięczny zysk? Załóżmy, że można wygenerować ułamkową liczbę jednostek.
-
Zakład produkcji komputerowej produkuje myszy, klawiatury i joysticki gier wideo. W poniższej tabeli podano zysk jednostkowy, użycie na jednostkę pracy, miesięczne zapotrzebowanie i użycie na jednostkę czasu maszynowego:
Myszy
Klawiatury
Joysticki
Zysk/jednostka
$8
11 zł
$9
Użycie pracy/jednostka robocza
0,2 godziny
0,3 godziny
0,24 godziny
Czas/jednostka maszyny
0,04 godziny
0,055 godziny
0,04 godziny
Miesięczne zapotrzebowanie
15 000
27,000
11,000
-
Każdego miesiąca dostępne są łącznie 13 000 godzin pracy i 3000 godzin czasu pracy maszyny. Jak producent może zmaksymalizować swój miesięczny wkład zysku z zakładu?
-
Rozwiąż nasz przykład leku przy założeniu, że minimalne zapotrzebowanie na 200 jednostek dla każdego leku musi zostać spełnione.
-
Jason robi diamentowe bransoletki, naszyjniki i kolczyki. Chce pracować maksymalnie 160 godzin miesięcznie. Ma 800 uncji diamentów. Zysk, czas pracy i uncje diamentów wymaganych do produkcji każdego produktu są podane poniżej. Jeśli popyt na każdy produkt jest nieograniczony, w jaki sposób Jason może zmaksymalizować swój zysk?
Produkt
Zysk jednostkowy
Godziny pracy na jednostkę
Uncje diamentów na jednostkę
Bransoletka
300 zł
.35
1,2
Naszyjnik
200 zł
.15
.75
Kolczyki
100 zł
0,05
.5










