Zwraca wartość testu niezależności. Funkcja TEST.CHI zwraca wartość rozkładu chi-kwadrat (χ2) statystyki i stosownych stopni swobody. Testu χ2 można używać do określania, czy dane eksperymentalne potwierdzają przewidywania wynikające z hipotezy.
Ważne: Tę funkcję zamieniono na jedną lub więcej nowych funkcji, które mogą zapewniać większą dokładność i mają nazwy lepiej oddające ich przeznaczenie. Mimo że ta funkcja jest wciąż dostępna w celu zachowania zgodności z wcześniejszymi wersjami programu, należy rozważyć rozpoczęcie korzystania z nowych funkcji, ponieważ ta funkcja może być niedostępna w przyszłych wersjach programu Excel.
Aby uzyskać więcej informacji na temat nowej funkcji, zobacz temat CHI.TEST, funkcja.
Składnia
TEST.CHI(zakres_rzeczywisty;zakres_przewidywany)
W składni funkcji TEST.CHI występują następujące argumenty:
-
Zakres_rzeczywisty Argument wymagany. Zakres danych zawierający wartości obserwowane, które należy porównać z wartościami przewidywanymi.
-
Zakres_przewidywany Argument wymagany. Zakres danych zawierający współczynnik iloczynu sum wierszy i sum kolumn do sumy końcowej.
Spostrzeżenia
-
Jeśli argumenty zakres_rzeczywisty i zakres_przewidywany mają różne liczby punktów danych, funkcja TEST.CHI zwraca wartość błędu #N/D!.
-
W teście χ2 najpierw jest obliczana statystyka χ2 na podstawie równania:
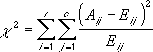
gdzie:
Aij = rzeczywista częstość w i-tym wierszu j-tej kolumny
Eij = przewidywana częstość w i-tym wierszu j-tej kolumny
r = liczba wierszy
c = liczba kolumn
-
Mała wartość χ2 oznacza niezależność. Równanie pokazuje, że wartość χ2 jest zawsze większa od zera lub równa zero, a ten drugi przypadek ma miejsce wtedy i tylko wtedy, gdy Aij = Eij dla każdego i,j.
-
Funkcja TEST.CHI zwraca prawdopodobieństwo tego, że przy założeniu niezależności wartość statystyki χ2 będzie mniejsza lub równa od wartości obliczonej na podstawie powyższego wzoru. W obliczeniach jest wykorzystywany rozkład χ2 o odpowiedniej liczbie stopni swobody, ss. Jeśli r > 1 i c > 1, to ss = (r - 1)(c - 1). Jeśli r = 1 i c > 1, to ss = c - 1, a jeśli r > 1 i c = 1, to ss = r - 1. Wartości r = c = 1 nie są dozwolone (w takim wypadku jest zwracany błąd #N/D).
-
Funkcja TEST.CHI powinna być stosowana, gdy wartości Eij nie są zbyt małe. Według niektórych ekspertów wszystkie wartości Eij powinny być większe lub równe 5.
Przykład
Skopiuj przykładowe dane z poniższej tabeli i wklej je w komórce A1 nowego arkusza programu Excel. Aby formuły wyświetlały wyniki, zaznacz je, naciśnij klawisz F2, a następnie naciśnij klawisz Enter. Jeśli to konieczne, możesz dostosować szerokości kolumn, aby wyświetlić pełne dane.
|
Mężczyźni (rzeczywiste) |
Kobiety (rzeczywiste) |
Opis |
|
58 |
35 |
Zgoda |
|
11 |
25 |
Neutralne |
|
10 |
23 |
Niezgoda |
|
Mężczyźni (przewidywane) |
Kobiety (przewidywane) |
Opis |
|
45,35 |
47,65 |
Zgoda |
|
17,56 |
18,44 |
Neutralne |
|
16,09 |
16,91 |
Niezgoda |
|
Formuła |
Opis |
Wynik |
|
=TEST.CHI(A2:B4;A6:B8) |
Statystyka χ2 dla powyższych danych jest równa 16,16957 przy 2 stopniach swobody. |
0,0003082 |










