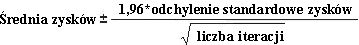Ten artykuł został zaadaptowany przez Wayne'a L. Winstona z analizy danych i modelowania biznesowego programu Microsoft Excel .
-
Kto korzysta z symulacji Monte Carlo?
-
Co się stanie, gdy wpiszesz =LOS() w komórce?
-
Jak można symulować wartości oddzielnej zmiennej losowej?
-
Jak można symulować wartości normalnej zmiennej losowej?
-
W jaki sposób firma zajmująca się kartami z pozdrowieniami może określić, ile kart należy wyprodukować?
Chcielibyśmy dokładnie oszacować prawdopodobieństwo niepewnych zdarzeń. Jakie jest na przykład prawdopodobieństwo, że przepływy gotówkowe nowego produktu będą miały dodatnią wartość bieżącą netto (NPV)? Jaki jest czynnik ryzyka naszego portfela inwestycyjnego? Symulacja Monte Carlo pozwala nam modelować sytuacje, które przedstawiają niepewność, a następnie odtwarzać je na komputerze tysiące razy.
Uwaga: Symulacja Monte Carlo pochodzi z symulacji komputerowych wykonanych w latach 30. Fizycy zaangażowani w tę pracę byli wielkimi fanami hazardu, więc dali symulacjom kod o nazwie Monte Carlo.
W kolejnych pięciu rozdziałach zobaczysz przykłady korzystania z programu Excel do przeprowadzania symulacji Monte Carlo.
Wiele firm korzysta z symulacji Monte Carlo jako ważnej części procesu decyzyjnego. Oto kilka przykładów.
-
General Motors, Proctor and Gamble, Pfizer, Bristol-Myers Squibb i Eli Lilly używają symulacji do oszacowania zarówno średniego zwrotu, jak i czynnika ryzyka nowych produktów. W GM informacje te są wykorzystywane przez dyrektora generalnego do określenia, które produkty wchodzą na rynek.
-
GM wykorzystuje symulacje do takich działań, jak prognozowanie dochodu netto przedsiębiorstwa, przewidywanie kosztów strukturalnych i zakupowych oraz określanie jego podatności na różne rodzaje ryzyka (takie jak zmiany stóp procentowych i wahania kursów wymiany).
-
Lilly wykorzystuje symulację do określenia optymalnej pojemności roślinnej dla każdego leku.
-
Proctor i Gamble korzystają z symulacji do modelowania i optymalnego zabezpieczania ryzyka walutowego.
-
Sears wykorzystuje symulacje, aby określić, ile jednostek każdej linii produktu należy zamówić od dostawców — na przykład liczba par spodni Dockers, które powinny zostać zamówione w tym roku.
-
Firmy naftowe i farmaceutyczne używają symulacji do wyceny "rzeczywistych opcji", takich jak wartość opcji rozszerzenia, zakontraktowania lub odroczenia projektu.
-
Planiści finansowi używają symulacji Monte Carlo do określenia optymalnych strategii inwestycyjnych na emeryturę swoich klientów.
Po wpisaniu formuły =LOS() w komórce zostanie wyświetlona liczba, która prawdopodobnie przyjmie dowolną wartość z przedziału od 0 do 1. W ten sposób, około 25 procent czasu, należy uzyskać liczbę mniejszą niż lub równą 0,25; około 10 procent czasu powinien zostać wyświetlony numer, który wynosi co najmniej 0,90 itd. Aby pokazać działanie funkcji LOS, przyjrzyj się Randdemo.xlsx pliku przedstawionemu na ilustracji 60-1.
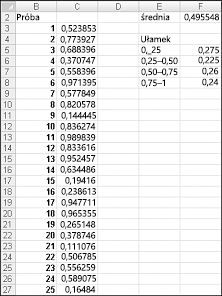
Uwaga: Po otwarciu pliku Randdemo.xlsx nie zobaczysz tych samych liczb losowych pokazanych na rysunku 60-1. Funkcja LOS zawsze automatycznie ponownie oblicza liczby wygenerowane po otwarciu arkusza lub po wprowadzeniu nowych informacji do arkusza.
Najpierw skopiuj z komórki C3 do komórki C4:C402 formułę =LOS(). Następnie należy nadać zakresowi C3:C402 Dane. Następnie w kolumnie F można śledzić średnią z 400 liczb losowych (komórka F2) i używać funkcji LICZ.JEŻELI do określenia ułamków z zakresu od 0 do 0,25, 0,25 i 0,50, 0,50 i 0,75 oraz 0,75 i 1. Po naciśnięciu F9 liczby losowe są obliczane ponownie. Zwróć uwagę, że średnia z 400 liczb jest zawsze w przybliżeniu 0,5, a około 25 procent wyników jest w interwałach 0,25. Wyniki te są zgodne z definicją liczby losowej. Należy również pamiętać, że wartości generowane przez los w różnych komórkach są niezależne. Jeśli na przykład liczba losowa wygenerowana w komórce C3 jest dużą liczbą (na przykład 0,99), nic nie informuje nas o wartościach innych generowanych liczb losowych.
Załóżmy, że zapotrzebowanie na kalendarz podlega następującej oddzielnej zmiennej losowej:
|
Popyt |
Prawdopodobieństwo |
|---|---|
|
10 000 |
0,10 |
|
20 000 |
0.35 |
|
40,000 |
0,3 |
|
60 000 |
0,25 |
Jak program Excel może odtwarzać lub symulować to zapotrzebowanie na kalendarze wiele razy? Sztuką jest skojarzenie każdej możliwej wartości funkcji LOS z możliwym zapotrzebowaniem na kalendarze. Poniższe zadanie gwarantuje, że zapotrzebowanie w wysokości 10 000 nastąpi w 10 procentach czasu i tak dalej.
|
Popyt |
Przypisana liczba losowa |
|---|---|
|
10 000 |
Mniej niż 0,10 |
|
20 000 |
Większe lub równe 0,10 i mniejsze niż 0,45 |
|
40,000 |
Większe lub równe 0,45 i mniejsze niż 0,75 |
|
60 000 |
Większe lub równe 0,75 |
Aby zademonstrować symulację popytu, spójrz na plik Discretesim.xlsx, pokazany na rysunku 60-2 na następnej stronie.
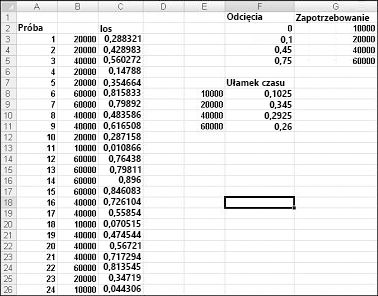
Kluczem do naszej symulacji jest użycie liczby losowej w celu zainicjowania wyszukiwania z zakresu tabeli F2:G5 (nazwanego odnośnika). Liczby losowe większe lub równe 0 i mniejsze niż 0,10 przyniosą popyt w wysokości 10 000; liczby losowe większe lub równe 0,10 i mniejsze niż 0,45 dadzą popyt w wysokości 20 000; liczby losowe większe lub równe 0,45 i mniejsze niż 0,75 dadzą popyt w wysokości 40 000; liczb losowych większych lub równych 0,75 spowoduje uzyskanie popytu w wysokości 60 000. Wygeneruj 400 liczb losowych, kopiując z komórki C3 do komórki C4:C402 formułę LOS(). Następnie wygenerujesz 400 prób lub iteracji zapotrzebowania na kalendarz, kopiując z komórki B3 do zakresu B4:B402 formułę WYSZUKAJ.PIONOWO(C3;odnośnik;2). Ta formuła gwarantuje, że każda liczba losowa mniejsza niż 0,10 generuje zapotrzebowanie na 10 000, a każda liczba losowa z przedziału od 0,10 do 0,45 generuje zapotrzebowanie w wysokości 20 000 itd. W zakresie komórek F8:F11 użyj funkcji LICZ.JEŻELI, aby określić ułamek naszych 400 iteracji dających każde żądanie. Kiedy naciskamy F9, aby ponownie obliczyć liczby losowe, symulowane prawdopodobieństwa są zbliżone do naszych zakładanych prawdopodobieństw popytu.
Wpisanie w dowolnej komórce formuły ROZKŁAD.NORMALNY.ODW(rand();mu;sigma)spowoduje wygenerowanie symulowanej wartości normalnej zmiennej losowej o średniej mł i odchyleniu standardowym sigma. Ta procedura jest zilustrowana w Normalsim.xlsx pliku przedstawioną na rysunku 60–3.
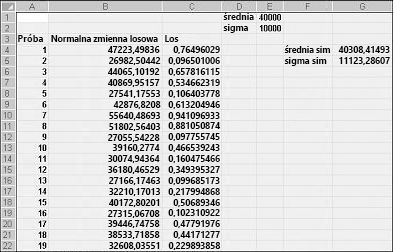
Załóżmy, że chcemy symulować 400 prób lub iteracji dla normalnej zmiennej losowej o średniej 40 000 i odchyleniu standardowym 10 000. (Możesz wpisać te wartości w komórkach E1 i E2 i nadać im nazwy odpowiednio średnią i sigma). Skopiowanie formuły =LOS() z komórki C4 do komórki C5:C403 generuje 400 różnych liczb losowych. Skopiowanie z komórki B4 do zakresu B5:B403 formuła ROZKŁAD.NORMALNY.ODW(C4;średnia;sigma) generuje 400 różnych wartości próbnych z normalnej zmiennej losowej o średniej 40 000 i odchyleniu standardowym 10 000. Po naciśnięciu F9 w celu ponownego obliczenia liczb losowych średnia pozostaje bliska 40 000, a odchylenie standardowe — blisko 10 000.
Zasadniczo dla liczby losowej x formuła ROZKŁAD.NORMALNY.ODW(p;mu;sigma) generuje p-typercentyl normalnej zmiennej losowej ze średnią m i odchyleniem standardowym sigma. Na przykład liczba losowa 0,77 w komórce C4 (patrz rysunek 60-3) generuje w komórce B4 w przybliżeniu 77 percentyl normalnej zmiennej losowej o średniej 40 000 i odchyleniu standardowym 10 000.
W tej sekcji zobaczysz, jak symulacja Monte Carlo może być używana jako narzędzie decyzyjne. Załóżmy, że zapotrzebowanie na kartkę walentynkową jest regulowane przez następującą oddzielną zmienną losową:
|
Popyt |
Prawdopodobieństwo |
|---|---|
|
10 000 |
0,10 |
|
20 000 |
0.35 |
|
40,000 |
0,3 |
|
60 000 |
0,25 |
Karta z pozdrowieniami sprzedaje się za $4.00, a zmienny koszt produkcji każdej karty wynosi $1.50. Karty resztkowe należy usunąć kosztem 0,20 USD za kartę. Ile kart należy wydrukować?
W zasadzie symulujemy każdą możliwą ilość produkcji (10 000, 20 000, 40 000 lub 60 000) wiele razy (na przykład 1000 iteracji). Następnie określamy, która ilość zamówień daje maksymalny średni zysk w stosunku do 1000 iteracji. Dane dotyczące tej sekcji można znaleźć w Valentine.xlsx pliku przedstawionej na ilustracji 60–4. Nazwy zakresów w komórkach B1:B11 są przypisywane do komórek C1:C11. Zakres komórek G3:H6 ma przypisany odnośnik nazwy. Nasze parametry ceny sprzedaży i kosztu są wprowadzane w komórkach C4:C6.
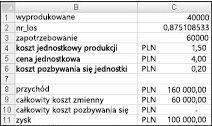
W komórce C1 można wprowadzić liczbę próbną produkcji (w tym przykładzie 40 000). Następnie utwórz liczbę losową w komórce C2 za pomocą formuły =LOS(). Jak opisano wcześniej, zasymulujesz zapotrzebowanie na kartę w komórce C3 za pomocą formuły WYSZUKAJ.PIONOWO(rand,odnośnik;2). (W formule WYSZUKAJ.PIONOWO los to nazwa komórki przypisana do komórki C3, a nie funkcja LOS).
Liczba sprzedanych jednostek jest mniejsza od naszej ilości produkcyjnej i popytu. W komórce C8 obliczasz nasze przychody za pomocą formuły MIN(wyprodukowany;popyt)*unit_price. W komórce C9 obliczasz całkowity koszt produkcji za pomocą formuły utworzonej*unit_prod_cost.
Jeśli produkujemy więcej kart niż jest popytu, liczba pozostałych jednostek równa się produkcji minus popyt; w przeciwnym razie żadne jednostki nie zostaną pominięte. Obliczamy nasz koszt usuwania w komórce C10 za pomocą formuły unit_disp_cost*JEŻELI(wyprodukowany>popytu;wyprodukowany–popyt;0). Na koniec w komórce C11 obliczamy zysk jako przychód — total_var_cost-total_disposing_cost.
Chcemy wydajnie naciskać F9 wiele razy (na przykład 1000) dla każdej ilości produkcyjnej i zliczać oczekiwany zysk dla każdej ilości. Jest to sytuacja, w której na ratunek przychodzi nam dwukierunkowa tabela danych. (Zobacz rozdział 15 "Analiza poufności z tabelami danych", aby uzyskać szczegółowe informacje o tabelach danych). Tabela danych użyta w tym przykładzie jest przedstawiona na rysunku 60–5.
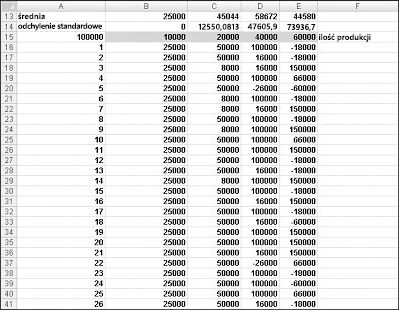
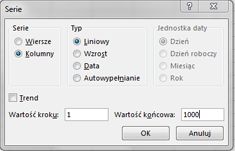
W zakresie komórek A16:A1015 wprowadź liczby od 1 do 1000 (odpowiadające 1000 próbom). Jednym z łatwych sposobów tworzenia tych wartości jest wprowadzenie wartości 1 w komórce A16. Zaznacz komórkę, a następnie na karcie Narzędzia główne w grupie Edytowanie kliknij pozycję Wypełnienie i wybierz pozycję Serie , aby wyświetlić okno dialogowe Seria . W oknie dialogowym Seria przedstawionym na rysunku 60–6 wprowadź wartość kroku 1 i wartość zatrzymania 1000. W obszarze Serie w wybierz opcję Kolumny , a następnie kliknij przycisk OK. Liczby od 1 do 1000 zostaną wprowadzone w kolumnie A, rozpoczynając od komórki A16.
Następnie wprowadzamy możliwe ilości produkcji (10 000, 20 000, 40 000, 60 000) w komórkach B15:E15. Chcemy obliczyć zysk dla każdej liczby próbnej (od 1 do 1000) i każdej ilości produkcyjnej. Odwołujemy się do formuły zysk (obliczonej w komórce C11) w lewej górnej komórce naszej tabeli danych (A15), wprowadzając formułę =C11.
Teraz możemy nakłonić program Excel do symulacji 1000 iteracji popytu na każdą ilość produkcji. Zaznacz zakres tabeli (A15:E1014), a następnie w grupie Narzędzia danych na karcie Dane kliknij pozycję Analiza warunkowa, a następnie wybierz pozycję Tabela danych. Aby skonfigurować dwukierunkową tabelę danych, wybierz ilość produkcyjną (komórkę C1) jako komórkę wprowadzania danych w wierszu i zaznacz dowolną pustą komórkę (wybraną przez nas komórkę I14) jako komórkę wprowadzania w kolumnie. Po kliknięciu przycisku OK program Excel symuluje 1000 wartości popytu dla każdej liczby zamówień.
Aby zrozumieć, dlaczego to działa, rozważ wartości umieszczone przez tabelę danych w zakresie komórek C16:C1015. W przypadku każdej z tych komórek program Excel użyje w komórce C1 wartości 20 000. W komórce C16 wartość komórki wejściowej kolumny 1 jest umieszczana w pustej komórce, a liczba losowa w komórce C2 jest obliczana ponownie. Odpowiedni zysk jest następnie rejestrowany w komórce C16. Następnie wartość wejściowa komórki kolumny 2 jest umieszczana w pustej komórce, a liczba losowa w komórce C2 ponownie oblicza się ponownie. Odpowiedni zysk zostanie wprowadzony w komórce C17.
Kopiując z komórki B13 do komórki C13:E13 formułę ŚREDNIA(B16:B1015)obliczamy średni symulowany zysk dla każdej ilości produkcyjnej. Kopiując z komórki B14 do komórki C14:E14 formuła ODCH.STANDARDOWE(B16:B1015)obliczamy odchylenie standardowe symulowanych zysków dla każdej liczby zamówień. Za każdym razem, gdy naciskamy F9, dla każdej liczby zamówień jest symulowanych 1000 iteracji popytu. Produkcja 40 000 kart zawsze daje największy oczekiwany zysk. Dlatego wydaje się, że produkcja 40 000 kart jest właściwą decyzją.
Wpływ ryzyka na naszą decyzję Jeśli wyprodukowaliśmy 20 000 zamiast 40 000 kart, nasz oczekiwany zysk spada o około 22 procent, ale nasze ryzyko (mierzone standardowym odchyleniem zysku) spada o prawie 73 procent. Dlatego, jeśli jesteśmy bardzo przeciwni ryzyku, produkcja 20 000 kart może być właściwą decyzją. Nawiasem mówiąc, produkcja 10 000 kart zawsze ma standardowe odchylenie 0 kart, ponieważ jeśli przedstawimy 10 000 kart, zawsze będziemy sprzedawać je wszystkie bez żadnych resztek.
Uwaga: W tym skoroszycie opcja Obliczanie jest ustawiona na Wartość automatyczna z wyjątkiem tabel. (Użyj polecenia Obliczanie w grupie Obliczanie na karcie Formuły). To ustawienie gwarantuje, że tabela danych nie zostanie ponownie obliczona, chyba że naciśniesz F9, co jest dobrym pomysłem, ponieważ duża tabela danych spowalnia pracę, jeśli będzie ponownie obliczana za każdym razem, gdy wpiszesz coś do arkusza. Zwróć uwagę, że w tym przykładzie po naciśnięciu F9 średnia zysk ulegnie zmianie. Dzieje się tak, ponieważ za każdym razem, gdy naciśniesz F9, do wygenerowania żądań dla każdej liczby zamówień zostanie użyta inna sekwencja 1000 liczb losowych.
Przedział ufności dla średniego zysku Naturalne pytanie, które należy zadać w tej sytuacji jest, w jakim przedziale jesteśmy 95 procent pewien, że prawdziwy średni zysk spadnie? Ten interwał jest nazywany przedziałem ufności 95 procent dla średniego zysku. Przedział ufności 95 procent średniej wyników symulacji jest obliczany za pomocą następującej formuły:
W komórce J11 oblicza się dolną granicę przedziału ufności 95 procent dla średniego zysku, gdy 40 000 kalendarzy zostanie wygenerowanych przy użyciu formuły D13–1,96*D14/PIERWIASTEK(1000). W komórce J12 obliczasz górną granicę interwału ufności 95 procent za pomocą formuły D13+1,96*D14/PIERWIASTEK(1000). Te obliczenia przedstawiono na rysunku 60–7.
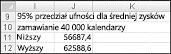
Jesteśmy w 95 procentach pewni, że średni zysk, gdy zamówionych jest 40 000 kalendarzy, wynosi od 56 687 do 62 589 zł.
-
Dealer GMC uważa, że popyt na wysłanników w 2005 r. będzie zwykle rozłożony ze średnią 200 i odchyleniem standardowym 30. Jego koszt otrzymania wysłannika wynosi 25.000 dolarów, a on sprzedaje wysłannika za 40.000 dolarów. Połowa wszystkich wysłanników nie sprzedanych w pełnej cenie można sprzedać za 30.000 dolarów. Rozważa zarządzenie 200, 220, 240, 260, 280 lub 300 wysłanników. Ilu powinien zamówić?
-
Mały supermarket próbuje ustalić, ile kopii Osoby magazynu powinni zamówić co tydzień. Uważają, że ich zapotrzebowanie na Osoby jest regulowane przez następującą oddzielną zmienną losową:
Popyt
Prawdopodobieństwo
15
0,10
20
0.20
25
0.30
30
0,25
35
0,15
-
Supermarket płaci 1,00 dolarów za każdą kopię Osoby i sprzedaje go za 1,95 dolarów. Każda niesprzedana kopia może zostać zwrócona w wysokości 0,50 USD. Ile kopii Osoby należy zamówić?
Potrzebujesz dodatkowej pomocy?
Zawsze możesz zadać pytanie ekspertowi w społeczności technicznej programu Excel lub uzyskać pomoc techniczną w Społecznościach.