Retorna a probabilidade de distribuição binomial do termo individual. Use DISTRBINOM em problemas com um número fixo de testes ou tentativas, quando os resultados de determinada tentativa forem apenas sucesso ou fracasso, quando as tentativas forem independentes e quando a probabilidade de sucesso for constante durante toda a experiência. Por exemplo, DISTRBINOM pode calcular a probabilidade de que dois dos próximos três bebês sejam meninos.
Importante: Essa função foi substituída por uma ou mais funções novas que podem oferecer mais precisão e cujos nomes refletem melhor o seu uso. Embora essa função ainda esteja disponível para compatibilidade com versões anteriores, recomenda-se o uso das funções novas de agora em diante, pois ela pode não estar disponível em versões futuras do Excel.
Para saber mais sobre a nova função, consulte Função DISTR.BINOM.
Sintaxe
DISTRBINOM(núm_s,tentativas,probabilidade_s,cumulativo)
A sintaxe da função DISTRBINOM tem os seguintes argumentos:
-
Núm_s Obrigatório. O número de tentativas bem-sucedidas.
-
Tentativas Obrigatório. O número de tentativas independentes.
-
Probabilidade_s Obrigatório. A probabilidade de sucesso em cada tentativa.
-
Cumulativo Obrigatório. Um valor lógico que determina a forma da função. Se cumulativo for VERDADEIRO, DISTRBINOM retornará a função de distribuição cumulativa, que é a probabilidade de que exista no máximo núm_s sucessos; se for FALSO, retornará a função massa de probabilidade, que é a probabilidade de que exista núm_s sucessos.
Comentários
-
Núm_s e tentativas são truncados para inteiros.
-
Se number_s, avaliações ou probability_s não for numérico, o BINOMDIST retornará o #VALUE! valor de erro.
-
Se number_s < 0 ou number_s > avaliações, BINOMDIST retornará o #NUM! valor de erro.
-
Se probability_s < 0 ou probability_s > 1, BINOMDIST retornará o #NUM! valor de erro.
-
Se x = número_s, n = tentativas e p = probabilidade_s, então a função de probabilidade de massa binomial é:
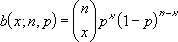
onde:

é COMBIN(n,x).
-
Se x = núm_s, n = tentativas, and p = probabilidade_s, então a função de distribuição binomial cumulativa é:
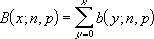
Exemplo
Copie os dados de exemplo da tabela a seguir e cole-os na célula A1 de uma nova planilha do Excel. Para as fórmulas mostrarem resultados, selecione-as, pressione F2 e pressione Enter. Se precisar, você poderá ajustar as larguras das colunas para ver todos os dados.
|
Dados |
Descrição |
|
|
6 |
O número de tentativas bem-sucedidas |
|
|
10 |
O número de tentativas independentes |
|
|
0,5 |
A probabilidade de sucesso em cada tentativa |
|
|
Fórmula |
Descrição |
Resultado |
|
=DISTRBINOM(A2;A3;A4;FALSO) |
Probabilidade de exatamente 6 de 10 tentativas serem bem-sucedidas |
0,2050781 |










