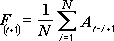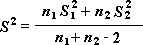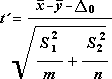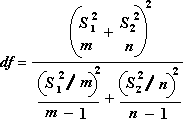Se for necessário criar análises estatísticas ou de engenharia complexas, é possível economizar etapas e tempo usando as Ferramentas de Análise. Você fornece os dados e parâmetros para cada análise, e a ferramenta utiliza as funções estatísticas ou de engenharia macro apropriadas para calcular e exibir os resultados em uma tabela de saída. Algumas ferramentas geram gráficos além das tabelas de saída.
As funções de análise de dados podem ser usadas apenas em uma planilha de cada vez. Quando você efetua a análise de dados em planilhas agrupadas, os resultados aparecerão na primeira planilha e tabelas formatadas vazias aparecerão nas planilhas restantes. Para executar uma análise de dados no restante das planilhas, recalcule a ferramenta de análise para cada planilha.
As Ferramentas de Análise incluem as ferramentas descritas abaixo. Para acessar essas ferramentas, clique em Análise de Dados no grupo Análise na guia Dados. Se o comando Análise de Dados não estiver disponível, carregue o programa suplementar Ferramentas de Análise.
-
Clique na guia Arquivo, em Opções e depois na categoria Suplementos.
-
Na caixa Gerenciar, selecione Suplementos do Excel e clique em Ir.
Se estiver usando o Excel para Mac, no menu arquivo, acesse Ferramentas > Suplementos do Excel.
-
Na caixa Suplementos, marque a caixa Ferramentas de Análise e clique em OK.
-
Se as Ferramentas de Análise não estiverem listadas na caixa Suplementos disponíveis, clique em Procurar para localizá-las.
-
Se você for avisado de que as Ferramentas de Análise não estão atualmente instaladas no computador, clique em Sim para instalá-las.
-
Observação: Para incluir funções de VBA (Visual Basic for Application) nas Ferramentas de Análise, você pode carregar o Suplemento de Ferramentas de Análise - VBA da mesma forma que carrega as Ferramentas de Análise. Na caixa Suplementos disponíveis, marque a caixa de seleção Ferramentas de Análise - VBA.
As ferramentas de análise Anova fornecem diferentes tipos de análise de variação. A ferramenta a ser usada dependerá do número de fatores e de amostras que você tem das populações que deseja testar.
Anova: Fator Único
Essa ferramenta executa uma análise simples de variação de dados para dois ou mais exemplos. A análise fornece um teste da hipótese de que cada exemplo é extraído da mesma distribuição de probabilidade subjacente em relação à hipótese alternativa de que as distribuições de probabilidade subjacentes não são iguais para todos os exemplos. Se houver apenas dois exemplos, você poderá usar a função de planilha T.TESTE. Com mais de dois exemplos, não há uma generalização conveniente de T.TEST e o modelo Anova de Fator Único podem ser chamados em vez disso.
Anova: Fator Duplo com Replicação
Esta ferramenta de análise é útil quando os dados podem ser classificados com base em duas dimensões diferentes. Por exemplo, em um experimento para medir a altura das plantas, estas podem receber diferentes marcas de fertilizantes (por exemplo, A, B, C) e também ser mantidas em temperaturas diferentes (por exemplo, baixa, alta). Para cada um dos seis pares possíveis de {fertilizante, temperatura}, é obtido um número igual de observações da altura das plantas. Usando esta ferramenta Anova, podemos testar:
-
Se as alturas das plantas no caso das diferentes marcas de fertilizantes são tiradas da mesma população de base. As temperaturas são ignoradas para essa análise.
-
Se as alturas das plantas no caso dos diferentes níveis de temperatura são tiradas da mesma população de base. As marcas de fertilizantes são ignoradas para essa análise.
Se, tendo observado os efeitos das diferenças entre as marcas de fertilizantes encontradas na etapa 1 e as diferenças nas temperaturas encontradas na etapa 2, as seis amostras que representam todos os pares de valores de {fertilizante, temperatura} são tirados da mesma população. A hipótese alternativa é de que existem efeitos causados por pares {fertilizante, temperatura} específicos, além das diferenças baseadas somente no fertilizante ou somente na temperatura.
Anova: Fator Duplo sem Replicação
Esta ferramenta de análise é útil quando os dados são classificados em duas dimensões diferentes como no caso do Fator Duplo com Replicação. Entretanto, para essa ferramenta, assumimos a existência de apenas uma única observação para cada par (por exemplo, cada par de {fertilizante, temperatura} do exemplo acima).
As funções de planilha CORREL e PEARSON calculam o coeficiente de correlação entre duas variáveis de medida quando as medidas em cada variável são observadas para cada um dos N assuntos. (Qualquer falta de observação de algum assunto fará com que ele seja ignorado na análise.) A ferramenta de análise Correlação é especialmente útil quando há mais de duas variáveis de medida para cada um dos N assuntos. Ela fornece uma tabela de saída, uma matriz de correlação, que mostra o valor de CORREL (ou PEARSON) aplicado a cada um dos possíveis pares de variáveis de medida.
O coeficiente de correlação, assim como a covariação, mede até que ponto duas variáveis de medida "variam juntas". Diferente da covariação, o coeficiente de correlação é dimensionado de modo que seu valor seja independente das unidades de expressão das duas variáveis de medida. (Por exemplo, se as duas variáveis de medida forem peso e altura, o valor do coeficiente de correlação permanecerá inalterado se o peso for convertido de libras em quilogramas.) O valor de qualquer coeficiente de correlação deve estar entre -1 e +1 inclusive.
Você pode usar a ferramenta de análise de correlação para examinar cada par de variáveis de medida a fim de determinar se as duas variáveis de medida tendem a se mover juntas — isto é, se os valores altos de uma variável tendem a ser associados aos valores altos da outra (correlação positiva), se os valores baixos de uma variável tendem a ser associados aos valores altos da outra (correlação negativa) ou se os valores das duas variáveis tendem a não estar relacionados (correlação próxima de zero).
As ferramentas correlação e covariância podem ser usadas na mesma configuração, quando você tem N variáveis de medida diferentes observadas em um conjunto de indivíduos. As ferramentas correlação e covariância fornecem cada uma uma tabela de saída, uma matriz, que mostra o coeficiente de correlação ou covariância, respectivamente, entre cada par de variáveis de medida. A diferença é que os coeficientes de correlação são dimensionados para ficar entre -1 e +1 inclusivos. As covariâncias correspondentes não são dimensionadas. Tanto o coeficiente de correlação quanto a covariância são medidas de até que ponto duas variáveis "variam juntas".
A ferramenta Covariance calcula o valor da função de planilha COVARIANCE. P para cada par de variáveis de medida. (Uso direto de COVARIANCE. P em vez da ferramenta Covariance é uma alternativa razoável quando há apenas duas variáveis de medida, ou seja, N=2.) A entrada na diagonal da tabela de saída da ferramenta Covariance na linha i, coluna i é a covariância da variável de medida i-th com ela mesma. Essa é apenas a variação populacional dessa variável, conforme calculado pela função de planilha VAR.P.
Você pode usar a ferramenta Covariação para examinar cada par de variáveis de medida a fim de determinar se as duas variáveis de medida tendem a se mover juntas — isto é, se os valores altos de uma variável tendem a ser associados aos valores altos da outra (covariação positiva), se os valores baixos de uma variável tendem a ser associados aos valores altos da outra (covariação negativa) ou se os valores das duas variáveis tendem a não estar relacionados (covariação próxima de zero).
A ferramenta de análise Estatística Descritiva gera um relatório de estatísticas univariáveis dos dados no intervalo de entrada, fornecendo informações sobre a tendência e a variabilidade centrais dos dados.
A ferramenta de análise Ajuste Exponencial prevê um valor com base na previsão do período anterior, ajustado para o erro nessa previsão anterior. A ferramenta usa a constante de ajuste a, cuja magnitude determina com que intensidade as previsões reagem aos erros na previsão anterior.
Observação: Valores de 0,2 a 0,3 são constantes de ajuste razoáveis. Estes valores indicam que a previsão atual deve ser ajustada 20 a 30% pelo erro da previsão anterior. Constantes maiores produzem uma resposta mais rápida, mas podem produzir projeções erráticas. Constantes menores podem resultar em longos atrasos para os valores de previsão.
A ferramenta de análise Teste-F com Amostra Dupla para Variações executa um teste-F com amostra dupla para comparar duas variações de população.
Por exemplo, você pode usar a ferramenta Teste-F em amostras dos tempos em uma competição de natação para cada uma de duas equipes. A ferramenta fornece o resultado de um teste da hipótese nula de que essas duas amostras são provenientes de distribuições com variações iguais contra a alternativa de que as variações não são iguais nas distribuições de base.
A ferramenta calcula o valor f de uma estatística F (ou proporção F). Um valor f próximo de 1 fornece evidências de que as variações na população de base são iguais. Na tabela de saída, se f < 1 "P(F <= f) uni-caudal" fornecerá a probabilidade de observar um valor da estatística F menor que f quando as variações de população forem iguais, e "F Crítico uni-caudal" fornecerá o valor crítico menor que 1 para o nível de significância escolhido, Alfa. Se f > 1, "P(F <= f) uni-caudal" fornecerá a probabilidade de observar um valor da estatística F maior que f quando as variações de população forem iguais, e "F Crítico uni-caudal" fornecerá o valor crítico maior que 1 para Alfa.
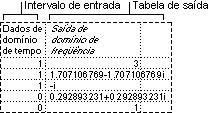
A ferramenta Análise de Fourier resolve problemas em sistemas lineares e analisa dados periódicos usando o método FFT (Transformação de Fourier Rápida) para transformar os dados. Esta ferramenta também efetua transformações inversas em que o inverso dos dados transformados retorna os dados originais.
A ferramenta de análise Histograma calcula frequências individuais e cumulativas de um intervalo de dados e de vínculos de dados em células. Esta ferramenta gera dados para o número de ocorrências de um valor em um conjunto de dados.
Por exemplo, em uma turma de 20 alunos, você pode definir a distribuição dos resultados em categorias de notas em letras. Uma tabela do histograma apresenta os limites de notas em letras e o número de pontos entre o limite mais baixo e o limite atual. O resultado único mais frequente é o modo dos dados.
Dica: No Excel 2016, agora você pode criar um gráfico de histograma ou de Pareto.
A ferramenta de análise Média Móvel projeta valores no período de previsão, com base no valor da média da variável em um número específico de períodos precedentes. Uma média móvel fornece informações de tendência que uma média simples de todos os dados históricos não revela. Use esta ferramenta para prever vendas, dados em inventário ou outras tendências. Cada valor de previsão baseia-se na seguinte fórmula:
onde:
-
N é o número de períodos anteriores para incluir na média móvel
-
A j é o valor real no período de tempo j
-
F j é o valor previsto no período de tempo j
A ferramenta de análise Geração de Números Aleatórios preenche um intervalo com números aleatórios independentes tirados de uma dentre várias distribuições. Você pode usar esta ferramenta para caracterizar indivíduos em uma população com uma distribuição de probabilidade. Por exemplo, você pode usar uma distribuição normal para caracterizar a população de alturas dos indivíduos ou pode usar uma distribuição de Bernoulli de dois resultados possíveis para caracterizar a população de resultados de "cara ou coroa".
A ferramenta de análise Classificação e Percentil produz uma tabela que contém a classificação ordinal e percentual de cada valor num conjunto de dados. Pode analisar a posição relativa dos valores num conjunto de dados. Esta ferramenta utiliza as funções de folha de cálculo ORDEM. EQ eORDEM.PERCENTUAL. INC. Se quiser contabilizar os valores associados, utilize a função ORDEM. A função EQ , que trata os valores associados como tendo a mesma classificação, ou utiliza a função ORDEM.Função AVG , que devolve a classificação média dos valores associados.
A ferramenta de análise Regressão executa uma análise de regressão linear usando o método de "quadrados mínimos" para ajustar uma linha em um conjunto de observações. Você pode analisar como uma única variável dependente é afetada pelos valores de uma ou mais variáveis independentes. Por exemplo, você pode analisar como o desempenho de um atleta é afetado por fatores como idade, altura e peso. Você pode ratear porções na medida do desempenho para cada um desses três fatores, com base em um conjunto de dados de desempenho e usar os resultados para prever o desempenho de um atleta novo ainda não testado..
A ferramenta Regressão utiliza a função de folha de cálculo PROJ.LIN.
A ferramenta de análise Amostragem cria uma amostra de uma população tratando o intervalo de entrada como uma população. Quando a população for grande demais para processar ou criar um gráfico, você pode usar uma amostra representativa. Também é possível criar uma amostra que contém apenas os valores de determinada parte de um ciclo se você achar que os dados de entrada são periódicos. Por exemplo, se o intervalo de entrada contiver números de vendas trimestrais, a amostragem com uma taxa periódica de 4 coloca os valores do mesmo trimestre no intervalo de saída.
As ferramentas de análise Teste-t com Amostra Dupla testam a igualdade das médias de população de base em cada amostra. As três ferramentas empregam diferentes suposições: de que as variações de população são iguais, de que as variações de população não são iguais e de que as duas amostras representam observações dos mesmos assuntos antes e depois do tratamento.
No caso das três ferramentas abaixo, um valor da estatística t, t, é calculado e mostrado como "t Stat" nas tabelas de saída. Dependendo dos dados, esse valor, t, poderá ser negativo ou não. Considerando médias de população de base iguais, se t < 0, "P(T <= t) uni-caudal" fornecerá a probabilidade de um valor da estatística t ser observado como mais negativo que t. Se t >=0, "P(T <= t) uni-caudal" fornecerá a probabilidade de um valor da estatística t ser observado como mais positivo que t. "t Crítico uni-caudal" fornecerá o valor de corte para que a probabilidade de um valor da estatística t maior ou igual a "t Crítico uni-caudal" ser observado seja Alfa.
"P(T <= t) bicaudal" fornece a probabilidade de um valor da estatística t ser observado como maior em valor absoluto do que t. "P Crítico bicaudal" fornece o valor de corte para que a probabilidade de uma estatística t observada, maior em valor absoluto do que "P Crítico bicaudal", seja Alfa.
Teste-t: Amostra Dupla em Par para Médias
Você pode usar um teste em par quando houver um emparelhamento natural de observações nas amostras, como no caso em que um grupo de amostras é testado duas vezes — antes e depois de um experimento. Esta ferramenta de análise e sua fórmula executam um teste-t de estudantes com amostra dupla em par para determinar se as observações feitas antes e após um tratamento têm probabilidade de serem provenientes de distribuições com médias de população iguais. Esta forma de Teste-t não presume que as variações das duas populações sejam iguais.
Observação: Entre os resultados gerados por esta ferramenta está a variação agrupada, uma medida acumulada da distribuição dos dados na média, derivada da seguinte fórmula.
Teste-t: Amostra Dupla Presumindo Variações Equivalentes
Esta ferramenta de análise executa um teste-t de estudantes com amostra dupla. Essa forma de Teste-t presume que os dois conjuntos de dados são provenientes de distribuições com as mesmas variações. Ela é chamada de teste-t homoscedástico. Você pode usar esse teste para determinar se existe alguma probabilidade de as duas amostras serem provenientes de distribuições com médias de população iguais.
Teste-t: Amostra Dupla Presumindo Variações Diferentes
Esta ferramenta de análise executa um teste-t de estudantes com amostra dupla. Essa forma de Teste-t presume que os dois conjuntos de dados são provenientes de distribuições com variações diferentes. Ela é chamada de teste-t heteroscedástico. Da mesma forma que no caso de variações iguais acima, você pode usar esse teste-t para determinar se existe alguma probabilidade de as duas amostras serem provenientes de distribuições com médias de população iguais. Use esse teste quando houver assuntos distintos nas duas amostras. Use o teste em par, descrito abaixo, quando houver um único conjunto de assuntos e as duas amostras representarem medidas de cada assunto antes e depois de um tratamento.
A fórmula a seguir é usada para determinar o valor estatístico t.
A fórmula seguinte é utilizada para calcular os graus de liberdade, df. Uma vez que o resultado do cálculo não é normalmente um número inteiro, o valor de df é arredondado para o número inteiro mais próximo para obter um valor crítico da tabela t. A função de folha de cálculo do Excel T.TEST utiliza o valor df calculado sem arredondamento, porque é possível calcular um valor para T.TESTE com um noninteger df. Devido a estas diferentes abordagens para determinar os graus de liberdade, os resultados de T.TESTE e esta ferramenta t-Test irão diferir no caso Variâncias Desiguais.
A ferramenta de análise z-Test: Two Sample for Means efetua um teste z de dois exemplos para meios com variâncias conhecidas. Esta ferramenta é utilizada para testar a hipótese nula de que não existe diferença entre duas médias de população em relação a hipóteses alternativas unilaterais ou de dois lados. Se as variâncias não forem conhecidas, a função da folha de cálculo Z.O TESTE deve ser utilizado.
Ao utilizar a ferramenta Teste-z, o usuário deverá tomar cuidado para entender a saída. "P(Z <= z) uni-caudal" é realmente P(Z >= ABS(z)), a probabilidade de um valor de z mais distante de 0 na mesma direção que o valor de z observado quando não há diferença entre as médias de população. "P(Z <= z) bicaudal" é realmente P(Z >= ABS(z) ou Z <= -ABS(z)), a probabilidade de um valor de z mais distante de 0, em qualquer direção em relação ao valor de z observado quando não há diferença entre as médias de população. O resultado bicaudal é simplesmente o resultado uni-caudal multiplicado por 2. A ferramenta Teste-z também pode ser usada para o caso em que a hipótese nula for de que existe um valor específico diferente de zero para a diferença entre as médias das duas populações. Por exemplo, você pode usar esse teste para determinar as diferenças entre o desempenho de dois modelos de carro.
Precisa de mais ajuda?
Você pode sempre consultar um especialista na Excel Tech Community ou obter suporte nas Comunidades.
Confira também
Criar um histograma no Excel 2016
Criar um gráfico Pareto no Excel 2016
Carregar o Analysis ToolPak no Excel
Funções ENGINEERING (referência)
Visão geral de fórmulas no Excel
Como evitar fórmulas quebradas
Localizar e corrigir erros em fórmulas
Atalhos do teclado e teclas de função do Excel