CONFIDENCE.NORM (funcția CONFIDENCE.NORM)

Descriere

Intervalul de încredere este un interval de valori. Media eșantionului, x, este la centrul acestui interval, iar intervalul este x ± CONFIDENCE.NORM. De exemplu, dacă x este media pe eșantion a perioadelor de livrare pentru produsele comandate prin poștă, x ± CONFIDENCE.NORM este un interval al mediilor populației. Pentru orice medie a populației, µ0, care este în acest interval, probabilitatea obținerii unei medii a eșantionului mai depărtată de µ0 decât x este mai mare decât alfa; pentru orice medie a populației, µ0, care nu este în acest interval, probabilitatea obținerii unei medii a eșantionului mai depărtată de µ0 decât x este mai mică decât alfa. Cu alte cuvinte, presupunem că utilizăm x, abatere_standard și dimensiune pentru a construi un test bilateral la nivelul de semnificație alfa a ipotezei că media populației este µ0. Atunci nu vom respinge ipoteza dacă µ0 este în intervalul de încredere și o vom respinge dacă µ0 nu este în intervalul de încredere. Intervalul de încredere nu permite să tragem concluzia că există o probabilitate 1 – alfa ca următoarea livrare să aibă o perioadă de livrare în intervalul de încredere.

Sintaxă

CONFIDENCE.NORM(alfa,dev_standard,dimensiune)

Sintaxa funcției CONFIDENCE.NORM are următoarele argumente:

• Alfa     Obligatoriu. Este nivelul de semnificație utilizat pentru a calcula nivelul de încredere. Nivelul de semnificație este egal cu 100*(1 - alfa)%, cu alte cuvinte, o valoare alfa de 0,05 indică un nivel de încredere de 95 procente.

• Dev_standard     Obligatoriu. Este abaterea standard a populației pentru zona de date și se presupune a fi cunoscută.

• Dimensiune     Obligatoriu. Este mărimea eșantionului.

Observații

• Dacă vreun argument nu este numeric, CONFIDENCE. NORM returnează #VALUE! .

• Dacă alfa ≤ 0 sau alfa ≥ 1, CONFIDENCE. NORM returnează #NUM! .

• Dacă standard_dev ≤ 0, CONFIDENCE. NORM returnează #NUM! .

• Dacă size nu este un întreg, se trunchiază.

• Dacă dimensiune < 1, CONFIDENCE. NORM returnează #NUM! .

• Dacă presupunem alfa egal 0,05, trebuie să calculăm aria de sub curba normală standard, care este (1 - alfa) sau 95 procente. Această valoare este ±1,96. De aceea, intervalul de încredere este:

  

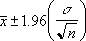
Exemplu

Copiați datele din exemplele din următorul tabel și lipiți-le în celula A1 a noii foi de lucru Excel. Pentru ca formulele să afișeze rezultate, selectați-le, apăsați pe F2, apoi pe Enter. Dacă trebuie, puteți ajusta lățimea coloanei pentru a vedea toate datele.