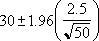Întoarce intervalul de încredere pentru o medie a populației cu o repartiție normală. Intervalul de încredere este o zonă de fiecare parte a unei medii a eșantionului. De exemplu, dacă comandați un produs prin e-mail, puteți determina, cu un anumit nivel de încredere, că va sosi cel mai devreme și mai recent produs.
Sintaxă
CONFIDENCE(alfa,standard_dev,dimensiune)
Alfa este nivelul de semnificație utilizat pentru a calcula nivelul de încredere. Nivelul de semnificație este egal cu 100*(1 - alfa)%, cu alte cuvinte, o valoare alfa de 0,05 indică un nivel de încredere de 95 procente.
Dev_standard este abaterea standard a populației pentru zona de date și se presupune a fi cunoscută.
Dimensiune este dimensiunea eșantionului.
Observații
-
Dacă vreun argument nu este numeric, CONFIDENCE întoarce #VALUE! .
-
Dacă alfa ≤ 0 sau alfa ≥ 1, CONFIDENCE returnează #NUM! .
-
Dacă standard_dev ≤ 0, CONFIDENCE returnează #NUM! .
-
Dacă size nu este un întreg, se trunchiază.
-
Dacă dimensiune < 1, CONFIDENCE returnează #NUM! .
-
Dacă presupunem alfa egal 0,05, trebuie să calculăm aria de sub curba normală standard, care este (1 - alfa) sau 95 procente. Această valoare este ±1,96. De aceea, intervalul de încredere este:
Exemplu
Să presupunem că observăm că, în eșantionul nostru de 50 de navetiști, durata medie a călătoriei la locul de muncă este de 30 de minute cu o abatere standard a populației de 2,5. Putem fi siguri cu 95% că media populației este în intervalul:
|
Alfa |
StdDev |
Dimensiune |
Formulă |
Descriere (Rezultat) |
|---|---|---|---|---|
|
0,05 |
.5 |
50 |
=CONFIDENCE([Alfa],[StdDev],[Dimensiune]) |
Intervalul de încredere pentru o medie a populației. Cu alte cuvinte, durata medie de deplasare pentru a lucra este egală cu 30 ± 0,692951 minute sau de la 29,3 la 30,7 minute. (0.692951) |