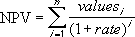NPV (funcția NPV)

Sintaxă

NPV(rată,valoare1,valoare2,...)

Rată     este rata de reducere pe o perioadă.

Valoare1, valoare2,...     sunt de la 1 până la 29 de argumente care reprezintă plățile și venitul. Valoare1, valoare2,... trebuie să fie spațiat în mod egal în timp și să aibă loc la sfârșitul fiecărei perioade. NPV utilizează ordinea valorilor1, valoare2,... pentru a interpreta ordinea fluxurilor de numerar. Asigurați-vă că valorile plăților și încasărilor sunt introduse în succesiunea corectă. Argumentele care sunt numere, valori goale, logice sau reprezentări text ale numerelor sunt contorizate; argumentele care sunt valori de eroare sau text care nu pot fi traduse în numere sunt ignorate.

Observații

• Funcția NPV își începe calculele cu o perioadă înaintea primului flux de numerar (valoare1) și le termină cu ultimul flux de numerar din listă. Calculul funcției NPV se bazează pe fluxuri de numerar viitoare. Dacă primul flux de numerar are loc la începutul primei perioade, prima valoare trebuie adăugată la rezultatul dat de NPV și nu inclusă în argumentele de tip valoare. Pentru mai multe informații, vedeți exemplele de mai jos.

• Dacă n este numărul de fluxuri de numerar din lisa de argumente, formula pentru NPV este:

  

• NPV este asemănătoare cu funcția PV (valoarea actualizată). Diferența semnificativă dintre PV și NPV este că PV acceptă fluxuri de numerar care au loc fie la începutul, fie la sfârșitul perioadei. Spre deosebire de valorile variabile ale fluxurilor de numerar din cazul NPV, fluxurile de numerar din PV trebuie să fie constante pe toată perioada investiției. Pentru informații despre anuități și funcții financiare, vedeți PV.

Exemplul 1

În exemplul următor:

• Rată este rata anuală de actualizare.

• Valoare1 este costul inițial al investiției peste un an.

• Value2 este rezultatul din primul an.

• Value3 este rezultatul din al doilea an.

• Value4 este rezultatul din al treilea an.

În exemplu, includeți costul inițial de 10.000 lei ca una dintre valori, deoarece plata are loc la sfârșitul primei perioade.

Exemplul 2

În exemplul următor:

• Rată este rata anuală de actualizare. Aceasta poate reprezenta rata inflației sau rata dobânzii unei investiții concurente.

• Valoare1 este costul inițial al investiției peste un an.

• Value2 este rezultatul din primul an.

• Value3 este rezultatul din al doilea an.

• Value4 este rezultatul din al treilea an.

• Valoare5 este rentabilitatea din al patrulea an.

• Valoare6 este rezultatul din al cincilea an.

În exemplu, nu includeți costul inițial de 40.000 lei ca una dintre valori, deoarece plata are loc la începutul primei perioade.