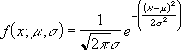Функция НОРМРАСП возвращает нормальное распределение для указанного среднего и стандартного отклонения. Эта функция имеет широкий спектр приложений в статистике, включая тестирование гипотез.
Важно: Эта функция была заменена вместе с другими функциями, которые могут обеспечить повышенную точность и имена которых лучше отражают их назначение. Эта функция остается доступной для обратной совместимости, но может быть недоступна в будущих версиях Excel. Теперь рассмотрите возможность использования новых функций.
Сведения о новой функции НОРМ.РАСП см. здесь.
Синтаксис
НОРМРАСП(x;среднее;стандартное_откл;интегральная)
Аргументы функции НОРМРАСП описаны ниже.
-
X Обязательный. Значение, для которого требуется распределение
-
Среднее Обязательный. Среднее арифметическое распределения
-
Стандартное_отклонение Обязательный. Стандартное отклонение распределения
-
Интегральная Обязательный. Логическое значение, определяющее форму функции. Если кумулятив имеет значение TRUE, НОРМРАСП возвращает функцию накопительного распределения; если совокупное значение равно FALSE, возвращается функция вероятностной массы.
Замечания
-
Если среднее или standard_dev не является числом, НОРМРАСП возвращает #VALUE! (значение ошибки).
-
Если standard_dev ≤ 0, НОРМРАСП возвращает #NUM! (значение ошибки).
-
Если среднее = 0, стандартное_откл = 1 и интегральная = ИСТИНА, то функция НОРМРАСП возвращает стандартное нормальное распределение, т. е. НОРМСТРАСП.
-
Уравнение для плотности нормального распределения (аргумент "интегральная" содержит значение ЛОЖЬ) имеет следующий вид:
-
Если аргумент "интегральная" имеет значение ИСТИНА, формула описывает интеграл с пределами от минус бесконечности до x.
Пример
Скопируйте пример Данные из следующей таблицы и вставьте его в ячейки A2 – A4 нового листа Excel. Скопируйте примеры формул НОРМРАСП в другие ячейки. Если результаты не отображаются автоматически, выберите формулы, нажмите клавишу F2 и клавишу ВВОД. При необходимости настройте ширину столбцов для видимости.
|
Данные |
Описание |
|
|---|---|---|
|
42 |
Значение, для которого нужно вычислить распределение |
|
|
40 |
Среднее арифметическое распределения |
|
|
1,5 |
Стандартное отклонение распределения |
|
|
Формула |
Описание |
Результат |
|
=НОРМРАСП(A2;A3;A4;ИСТИНА) |
Интегральная функция распределения для приведенных выше условий |
0,9087888 |
|
=НОРМРАСП(A2;A3;A4;ЛОЖЬ) |
Функция плотности распределения для приведенных выше условий |
0,10934 |