Važno: Podrška za Office 2016 i Office 2019 završila se 14. oktobra 2025. Izvršite nadogradnju na Microsoft 365 da biste radili bilo gde sa bilo kog uređaja i da biste nastavili da dobijate podršku. Nabavite Microsoft 365
Ovaj članak govori o korišćenju programskog dodatka Solver, programskog dodatka za Microsoft Excel koji možete da koristite za analizu šta-ako, da biste utvrdili optimalnu mešavinu proizvoda.
Kako da odredim mesečnu mešavinu proizvoda koja uvećava profitabilnost?
Preduzeća često treba da odrede količinu svakog proizvoda za proizvodnju na mesečnom nivou. U svom najjednostavnijem obliku , problem sa mešavinom proizvoda uključuje kako utvrditi količinu svakog proizvoda koji treba da se proizvodi tokom jednog meseca kako bi se povećao profit. Mešavina proizvoda obično mora da se pridrža sledećih ograničenja:
-
Mešavina proizvoda ne može da koristi više resursa nego što je dostupno.
-
Postoji ograničena potražnja za svaki proizvod. Ne možemo da proizvedemo više proizvoda tokom mesec dana nego što zahtevamo, jer je suvišna proizvodnja trajna (na primer, droge koja se može izneti).
Hajde da sada rešimo sledeći primer problema sa mešavinom proizvoda. Rešenje ovog problema možete da pronađete u odeljku Prodmix.xlsx, prikazanoj na slici 27-1.
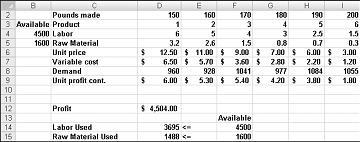
Recimo da radimo za kompaniju koja proizvodi šest različitih proizvoda u njihovoj fabrici. Proizvodnja svakog proizvoda zahteva rad i sirovinu. Red 4 na slici 27-1 prikazuje radno vreme potrebno za proizvodnju funte svakog proizvoda, a 5. red prikazuje funte sirovina potrebnih za proizvodnju funte svakog proizvoda. Na primer, za proizvodnju funte proizvoda 1 potrebno je šest sati rada i 3,2 funte sirovine. Za svaki lek cena po funti je data u redu 6, cena po jedinici po funti je data u redu 7, a doprinos za profit po funti je dat u redu 9. Na primer, "Proizvod 2" prodaje se za 11,00 USD po funti, nanosi cenu po jedinici od 5,70 USD po funti i doprinosi 5,30 USD profita po funti. Mesečni zahtev za svaki lek dat je redom 8. Na primer, zahtev za proizvod 3 je 1041 funti. Ovog meseca je na raspolaganju 4.500 sati rada i 1600 funti sirovina. Kako ovo preduzeće može da uveća mesečnu zarade?
Ako ne znamo ništa o programu Excel Solver, napali bismo ovaj problem pravljenjem radnog lista za praćenje upotrebe profita i resursa povezanih sa mešavinom proizvoda. Zatim bismo koristili probnu verziju i grešku da bismo menjali mešavinu proizvoda da bismo optimizovali profit bez korišćenja više rada ili sirovina nego što je dostupno, i bez proizvodnje bilo kakve droge prekomerne potražnje. Programski dodatak "Rešavač" koristimo u ovom procesu samo u fazi probne verzije i greške. U suštini, "Rešavač" je mašina za optimizaciju koja besprekono izvršava pretragu probne verzije i greške.
Za rešavanje problema sa mešavinom proizvoda ključno je da efikasno izračunavanje upotrebe resursa i profita povezanih sa bilo kojim datim mešavinom proizvoda. Važna alatka koju možemo da koristimo za pravljenje ovog SUMPRODUCT funkcije. Funkcija SUMPRODUCT množi odgovarajuće vrednosti u opsezi ćelija i daje zbir tih vrednosti. Svaki opseg ćelija koji se koristi u proceni SUMPRODUCT mora da ima iste dimenzije, što podrazumeva da možete da koristite SUMPRODUCT sa dva reda ili dve kolone, ali ne i sa jednom kolonom i jednim redom.
Kao primer toga kako možemo da koristimo funkciju SUMPRODUCT u primeru mešavine proizvoda, hajde da pokušamo da izračunavanje upotrebe resursa. Naše korišćenje rada izračunava
(Laboratorija je koristila funta droge 1)*(proizvodi se lek 1 funta)+ (Laboratorija je iskorišćena po funti droge 2)*(Proizvodi se lek 2 funte) + ... (Laboratorija je koristila po funti droge 6)*(proizvodi se lek 6 funti)
Možemo da računamo upotrebu rada na zamoniji način kao D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Slično tome, upotreba sirovina može da se izračuna kao D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Međutim, unos ovih formula u radni list za šest proizvoda oduže vreme. Zamislite koliko dugo bi vam bilo potrebno da radite sa preduzećem koje je proizvelo, na primer 50 proizvoda u njihovoj elektrani. Mnogo lakši način za računanje rada i sirove upotrebe materijala jeste kopiranje iz ćelija D14 u D15 formulu SUMPRODUCT($D$2:$I$2,D4:I4). Ova formula računa D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (što je iskorišćenost rada), ali je mnogo lakše ući! Obratite pažnju na to da koristim znak $sa opsegom D2:I2 tako da kada kopiram formulu i dalje hvatam mešavinu proizvoda iz 2. reda. Formula u ćeliji D15 računa upotrebu sirovina.
Na sličan način, naš profit je određen
(Droga 1 profit po funti)*(Proizvodi se droge 1 funta) + (Droga 2 profita po funti)*(Proizvodi se droge 2 funte) + ... (Droga 6 profita po funti)*(Proizvodi se droge 6 funti)
Profit se lako izračunava u ćeliji D12 pomoću formule SUMPRODUCT(D9:I9,$D$2:$I$2).
Sada možemo da identifikujemo tri komponente modela mešavine proizvoda Solver.
-
Ciljna ćelija. Naš cilj je da uvećamo profit (izračunat u ćeliji D12).
-
Menjanje ćelija. Broj funti proizvedenih za svaki proizvod (naveden u opsegu ćelija D2:I2)
-
Ograničenja. Imamo sledeća ograničenja:
-
Nemojte koristiti više rada ili sirovina nego što je dostupno. To jestalno, vrednosti u ćelijama D14:D15 (iskorišćeni resursi) moraju biti manje ili jednake vrednostima u ćelijama F14:F15 (dostupni resursi).
-
Nemoj da proizvodiљ viљe droge nego љto traћi. To je zato što vrednosti u ćelijama D2:I2 (funte koje se proizvode od svakog leka) moraju biti manje ili jednake zahtevu za svaki lek (navedeni u ćelijama D8:I8).
-
Ne možemo da proizvedemo negativnu količinu bilo kog leka.
-
Pokazaću vam kako da unesete ciljnu ćeliju, promenite ćelije i ograničenja u Programski dodatak "Rešavač". Sve što treba da uradite jeste da kliknete na dugme "Reši" da biste pronašli mešavinu proizvoda koja uvećava profit!
Da biste počeli, izaberite karticu Podaci i u grupi Analiza kliknite na dugme Rešavač.
Napomena: Kao što je objašnjeno u poglavlju 26, "Uvod u optimizaciju pomoću programskog dodatka Excel Rešavač", programski dodatak "Rešavač" instalira se klikom na dugme "Microsoft Office", a zatim na dugme "Excel opcije", iza kojeg sledi programski dodaci. Na listi Upravljanje izaberite stavku Excel programski dodaci, potvrdite izbor u polju za potvrdu Programski dodatak "Rešavač", a zatim kliknite na dugme U redu.
Pojaviće se dijalog Parametri programskog dodatka Solver, kao što je prikazano na slici 27-2.
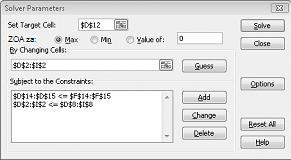
Kliknite na polje Postavi ciljnu ćeliju, a zatim izaberite ćeliju profita (ćelija D12). Potvrdite izbor u polju za potvrdu Promenom ćelija, a zatim postavite pokazivač na opseg D2:I2 koji sadrži funte proizvedenu od svakog leka. Dijalog bi sada trebalo da izgleda kao slika 27-3.
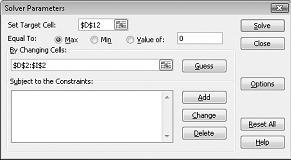
Sada smo spremni da dodamo ograničenja u model. Kliknite na dugme Dodaj. Videćete dijalog Dodavanje ograničenja koji je prikazan na slici 27-4.
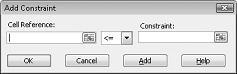
Da biste dodali ograničenja upotrebe resursa, kliknite na polje Referenca ćelije, a zatim izaberite opseg D14:D15. Izaberite <= sa srednje liste. Kliknite na polje Ograničenje, a zatim izaberite opseg ćelija F14:F15. Dijalog Dodavanje ograničenja sada bi trebalo da izgleda kao Slika 27-5.
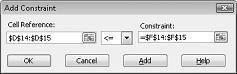
Sada smo obezbedili da kada programski dodatak "Rešavač" pokuša različite vrednosti za promenljene ćelije, biće u razmatranju samo kombinacije koje zadovoljavaju oba D14<=F14 (iskorišćeni rad je manji od ili jednak raspoloživoj radnoj površini) i biće u razmatranju D15<=F15 (iskorišćeni sirovina manje ili jednako dostupnom sirovinom). Kliknite na dugme Dodaj da biste uneli ograničenja zahteva. Popunjavanje dijaloga Dodavanje ograničenja kao što je prikazano na slici 27-6.
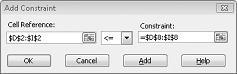
Ako dodate ova ograničenja, biće u razmatranju samo kombinacije koje zadovoljavaju sledeće parametre kada Programski dodatak "Rešavač" pokuša da izvrši različite kombinacije za promenljivih vrednosti ćelija:
-
D2<=D8 (količina proizvedenih narkotika 1 manja je od ili jednaka zahtevu za lekom 1)
-
E2<=E8 (količina proizvedenog leka 2 manja je od ili jednaka zahtevu za drogom 2)
-
F2<=F8 (iznos proizvedene droge 3 manji je od ili jednak zahtevu za lekom 3)
-
G2<=G8 (iznos proizvedene droge 4 manji je od ili jednak zahtevu za lekom 4)
-
H2<=H8 (iznos proizvedene droge 5 manji je od ili jednak zahtevu za drogom 5)
-
I2<=I8 (iznos proizvedene droge 6 manji je od ili jednak zahtevu za lek 6)
Kliknite na dugme U redu u dijalogu Dodavanje ograničenja. Prozor "Rešavač" bi trebalo da izgleda kao Slika 27-7.
Unosimo ograničenje da promene ćelija ne smeju biti negativne u dijalogu Opcije programskog dodatka Solver. Kliknite na dugme Opcije u dijalogu Parametri programskog dodatka Solver. Potvrdite izbor u poljima za potvrdu Pretpostavi linearni model i pretpostavi da nije negativan, kao što je prikazano na slici 27-8 na sledećoj stranici. Kliknite na dugme „U redu“.
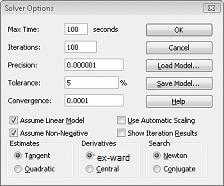
Ako potvrdite izbor u polju za potvrdu Pretpostavi da nije negativno, programski dodatak "Rešavač" uzima u obzir samo kombinacije promenljivih ćelija u kojima svaka promenljivih ćelija pretpostavlja vrednost koja nije negativna. Potvrdili smo izbor u polju za potvrdu Pretpostavi linearni model zato što je problem sa mešavinom proizvoda poseban tip problema "Rešavač" koji se zove linearni model. Model programskog dodatka "Rešavač" je u suštini linearni pod sledećim uslovima:
-
Ciljna ćelija se izračunava tako što se zajedno dodaju uslovi obrasca (promenska ćelija)*(konstanta).
-
Svako ograničenje zadovoljava "zahtev linearnog modela". To znači da se svako ograničenje procenjuje sabiranjem uslova obrasca (promenom ćelije )*( konstantom) i upoređivanjem zbirova sa konstantom.
Zašto je ovaj problem programskog dodatka "Rešavač" linearan? Naša ciljna ćelija (profit) je izračunata kao
(Droga 1 profit po funti)*(Proizvodi se droge 1 funta) + (Droga 2 profita po funti)*(Proizvodi se droge 2 funte) + ... (Droga 6 profita po funti)*(Proizvodi se droge 6 funti)
Ovo izračunavanje prati obrazac po kojem je vrednost ciljne ćelije izvedena tako što se dodaju zajedno termini obrasca (promenljivi ćelija)*(konstanta).
Ograničenje rada procenjuje se poređenjem vrednosti izvedene iz (Laboratorija je korišćena po funti droge 1)*(Narkotici 1 funti proizvedeni) + (Radna snaga iskorišćena po funti droge 2)*(Narkotici 2 funte proizvedeni )+ ... (Raduj nas)ed po funti droge 6)*(Lek 6 funti proizvodi se) za raspoloživu radnu snagu.
Stoga se ograničenje rada procenjuje sabiranjem uslova obrasca (promenom ćelije )*( konstantom) i upoređivanjem zbirova sa konstantom. I ograničenje rada i sirovine ispunjavaju zahteve linearnog modela.
Naša ograničenja zahteva uzimaju obrazac
(Proizvede se lek 1)<=(Potražnja za drogom 1) (Proizvodi se lek 2)<=(Potražnja za drogom 2) .(Proizvodi se lek 6)<=(Potražnja za drogom 6)
Svako ograničenje zahteva takođe zadovoljava zahtev linearnog modela zato što se svaki procenjuje tako što se zajedno dodaju uslovi obrasca (promenljivi ćelija )*( konstanta) i upoređivanje zbirova sa konstantom.
Pošto ste prikazali da je naš model mešavine proizvoda linearni model, zašto nas je briga?
-
Ako je model programskog dodatka "Rešavač" linearan i izaberemo opciju Pretpostavi linearni model, zagarantovano je da će solver pronaći optimalno rešenje za model "Rešavač". Ako model programskog dodatka "Rešavač" nije linearni, programski dodatak "Rešavač" može ili neće pronaći optimalno rešenje.
-
Ako je model programskog dodatka "Rešavač" linearan i izaberemo opciju Pretpostavi linearni model, "Rešavač" koristi veoma efikasan algoritam (jednostavni metod) da bi našao optimalno rešenje modela. Ako je model programskog dodatka "Rešavač" linearan i ne izaberemo opciju Pretpostavi linearni model, "Rešavač" koristi veoma neeficivan algoritam (metod GRG2) i može imati poteškoća u pronalaženju optimalnog rešenja modela.
Kada kliknete na dugme U redu u dijalogu Opcije programskog dodatka Solver, vraćamo se u glavni dijalog Rešavač, prikazan ranije u slikama 27-7. Kada kliknete na dugme Reši, rešavač izračunava optimalno rešenje (ako postoji) za model mešavine proizvoda. Kao što sam rekao u Poglavlju 26, optimalno rešenje za model mešavine proizvoda bio bi skup promenljivih vrednosti ćelija (funte proizvedenih od svakog leka) koji uvećava profit u skupu svih izvoрenih rešenja. Izmenljivo rešenje je skup promenljivih vrednosti ćelija koje zadovoljavaju sva ograničenja. Promenljive vrednosti ćelija prikazane u slici 27-9 su izvoženo rešenje zato što svi nivoi proizvodnje nisu negativni, nivoi proizvodnje ne premašuju zahtev, a upotreba resursa ne premašuje dostupne resurse.
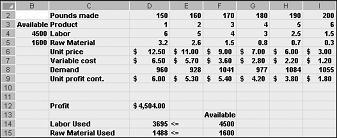
Promenljive vrednosti ćelija prikazane u slici 27-10 na sledećoj stranici predstavljaju neodoljivo rešenje iz sledećih razloga:
-
Proizvedemo viљe droge 5 nego љto traћimo.
-
Koristimo viљe rada nego ono љto je dostupno.
-
Koristimo više sirovina nego ono što je dostupno.
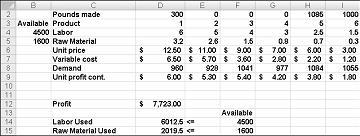
Kada kliknete na dugme Reši, Rešavač brzo pronalaži optimalno rešenje prikazano na slici 27-11. Potrebno je da izaberete stavku Zadrži rešenje programskog dodatka "Rešavač" da biste zadržali optimalne vrednosti rešenja u radnom listu.
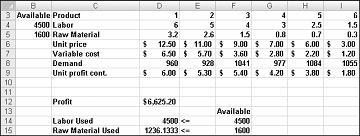
Naљa kompanija narkotika moћe da uveжa svoj mesečni profit na nivou od 6.625,20 usd proizvodnjom 596,67 funti droge 4, 1084 funte droge 5, i nijedne druge droge! Ne možemo da utvrdimo da li možemo da ostvarimo maksimalan profit od 6625,20 USD na drugi način. Sve u šta možemo da budemo sigurni je da sa ograničenim resursima i zahtevom ne možemo da napravimo više od 6.627,20 USD ovog meseca.
Pretpostavimo da se zahteva za svaki proizvod mora ispuniti. (Pogledajte radni list Bez izmenljivog rešenja u datoteci Prodmix.xlsx.) Zatim moramo da promenimo ograničenja zahteva iz D2:I2<=D8:I8 u D2:I2>=D8:I8. Da biste to uradili, otvorite Solver, izaberite ograničenje D2:I2<=D8:I8, a zatim kliknite na dugme Promeni. Pojavljuje se dijalog Promena ograničenja, prikazan u slici 27-12.
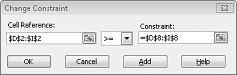
Izaberite >=, a zatim kliknite na dugme U redu. Sada smo se uverili da će "Rešavač" razmotriti promenu samo vrednosti ćelija koje ispunjavaju sve zahteve. Kada kliknete na dugme Reši, videćete poruku "Rešavač nije mogao da pronađe izlečeno rešenje". Ova poruka ne znači da smo pogrešili u modelu, već da sa ograničenim resursima ne možemo da ispunimo zahtev za sve proizvode. Rešavač nam jednostavno govori da ako želimo da ispunimo zahteve za svaki proizvod, moramo da dodamo više rada, više sirovina ili više od oba.
Da vidimo šta će se desiti ako dozvolimo neograničenu potražnju za svaki proizvod i dozvolimo da negativne količine budu proizvedeni od svake droge. (Ovaj problem programskog dodatka "Rešavač" možete videti na radnom listu "Postavljanje vrednosti ne konverguj " u datoteci Prodmix.xlsx.) Da biste pronašli optimalno rešenje za ovu situaciju, otvorite Rešavač, kliknite na dugme Opcije i opozovite izbor u polju za potvrdu Pretpostavi nenegativan. U dijalogu Parametri programskog dodatka Solver izaberite ograničenje zahteva D2:I2<=D8:I8, a zatim kliknite na dugme Izbriši da biste uklonili ograničenje. Kada kliknete na dugme Reši, Rešavač vraća poruku "Podesi vrednosti ćelija ne konverguj". Ova poruka znači da, ako ciljna ćelija treba da se uveća (kao u našem primeru), postoje izmenljiva rešenja sa proizvoljnim velikim vrednostima ciljnih ćelija. (Ako ciljna ćelija treba da se umanji, poruka "Postavljanje vrednosti ćelija ne konverguj" znači da postoje izobilazna rešenja sa proizvoljno malim vrednostima ciljnih ćelija.) U naљoj situaciji, dozvoljavajuжi negativnu proizvodnju leka, mi po pravimo resurse koji mogu da se koriste za proizvedene velike količine drugih droge. S tim naљim neograniиenim zahtevima, ovo nam omogućava da ostvarimo neograniиeni profit. U realnoj situaciji ne možemo da zaradimo beskonačnu količinu novca. Ukratko, ako vidite poruku "Postavi vrednosti ne konverguj", model sadrži grešku.
-
Recimo da naša kompanija narkotika može da kupi do 500 sati rada više od trenutnih troškova rada. Kako da uvećamo profit?
-
U postrojenju za proizvodnju čipova, četiri tehničara (A, B, C i D) proizvode tri proizvoda (Proizvodi 1, 2 i 3). Ovog meseca proizvođač čipova može da proda 80 jedinica proizvoda 1, 50 jedinica proizvoda 2 i najviše 50 jedinica proizvoda 3. Tehničar A može da napravi samo proizvode 1 i 3. Tehničar B može da napravi samo proizvode 1 i 2. Tehničar C može da napravi samo proizvod 3. Technician D može da napravi samo proizvod 2. Za svaku proizvodnu jedinicu proizvodi daju sledeći profit: Proizvod 1, 6 DIN; Proizvod 2, 7 DIN; i proizvod 3, 10 USD. Vreme (u časovima) koje je svakom tehničaru potrebno za proizvodnju proizvoda je sledeće:
Proizvod
Tehničar A
Tehničar B
Tehničar C
Technician D
1
2
2,5
Nije moguće izvršiti
Nije moguće izvršiti
2
Nije moguće izvršiti
3
Nije moguće izvršiti
3,5
3
3
Nije moguće izvršiti
4
Nije moguće izvršiti
-
Svaki tehničar može da radi do 120 sati mesečno. Kako proizvođač čipova može da uveća mesečnu zarudu? Pretpostavimo da može da se proizvede broj razlomka.
-
Fabrika za proizvodnju računara proizvodi miš, tastature i džojstike za video igre. Profit po jedinici, iskorišćenost rada po jedinici, mesečna potražnja i iskorišćenost mašinskog po jedinici navedeni su u sledećoj tabeli:
Miševi
Tastature
Džojstici
Profit/jedinica
8 DIN.
11 DIN.
9 USD
Upotreba radne snage/jedinica
.2 čas
.3 čas
.24 čas
Vreme/jedinica računara
.04 čas
.055 čas
.04 čas
Mesečna potražnja
15.000
27,000
11,000
-
Svakog meseca dostupno je ukupno 13.000 radnih sati i 3000 sati mašinskog vremena. Kako proizvođač može da uveća mesečni doprinos proizvodnje elektrane?
-
Reљite naљ primer droge pod pretpostavkom da minimalna potraћnja od 200 jedinica za svaki lek mora biti ispunjena.
-
Džejson pravi dijamantske narukvice, ogrlice i minđuše. Želi da radi najviše 160 sati mesečno. Ima 800 unce dijamanata. Profit, vreme rada i unce dijamanata potrebnih za proizvodnju svakog proizvoda navedeni su ispod. Ako je potražnja za svaki proizvod neograničena, kako Džejson može da uveća profit?
Proizvod
Profit po jedinici
Radno vreme po jedinici
Unce dijamanata po jedinici
Narukvicu
300 din
.35
1,2
Ogrlicu
200 din.
.15
.75
Minрuљe
100 RSD
0,05
.5










